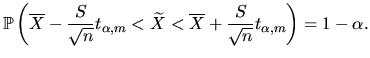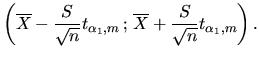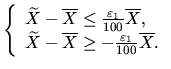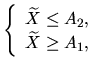методЭММ 21.06.2010. Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10

• Название: Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10
• Дата: 08.04.2022
• Размер: 0.98 Mb.
• Имя файла: методЭММ 21.06.2010.doc
• Тип: Методические указания; #454216
• страница: 5 из 7

Тема 5. Модели управления запасами

Эффективность деятельности торгового предприятия существенно зависит от величины товарных запасов (ТЗ).

Малый объем ТЗ затрудняет деятельность предприятия, а чрезмерно большой - приводит к большим издержкам на складские операции. Следовательно, возникает проблема ОУТЗ.

Рассмотрим эту задачу при следующих предположениях:

1) на складе хранятся товары одной группы;

2) спрос на товары известен и равномерен во времени;

3) поступление товара происходит в строго заказанное время с постоянной нормой;

4) стоимость складских операций состоит из затрат на хранение возникших товарных запасов и затрат на заказ.

Для составления модели введем следующие величины:

С₁ - затраты на хранение единицы товара в единицу времени, руб./кг сут.;

С₂ - затраты на заказ партии товара (не зависят от времени, от объема заказа), руб.;

r - норма спроса, кг/сут.;

k - норма завоза, кг/сут.;

u - количество товара, размещаемого в единице емкости склада (удельная емкость склада), кг/м³.

Задача ОУТЗ: Определить максимальный объем (V) заказываемой партии товара, при котором суточные затраты на складские операции в единицу времени будут минимальными (при условии что норма завоза товара превышает норму спроса на него).

Задача заключается в построении такой функции, которая будет зависеть от объема заказа Х и при этом будет выражаться через известные величины С₁, С₂, k, r, u и Q.

- суточные затраты на хранение товарных запасов за единицу времени,

- затраты на хранение товарных запасов в течение всего цикла Т;

- затраты на складские операции за весь цикл Т,
Тогда, чтобы выразить суточные затраты на складские операции нужно последнее выражение разделить на Т:

(31)

Так как за сутки товарные запасы увеличиваются на величину (k - r) и максимальный объем товарных запасов будет в момент времени t₀, т.е. когда весь объем заказа будет завезен в магазин, то максимальный объем товарных запасов рассчитывается по формуле:

(32)

В то же время за период t₀ весь объем заказа k будет завезен в магазин порциями по k единиц (тогда в течение периода времени t₀ весь заказ будет вывезен от поставщика), т.е.

- величина заказа, отсюда

- период времени завоза товара. (33)
Подставив (33) в (32), максимальный объем товарных запасов составит:

или (34)

Наряду с этим, за одни сутки продается r единиц товара. А всего объем заказанной партии X реализуется за период Т. Тогда

, отсюда - период цикла. (35)
Подставляя S^* и Т (т.е. (34) и (35)) в выражение (31), получим функцию отражающую суточные затраты на складские операции

. (36)

(37)

Х^* - максимальный объем заказываемой партии товара, рассчитанный без учета собственной емкости склада.

(38)

Х₁- максимальный объем заказа, рассчитанный с учетом собственной емкости склада.

Как только определились в объеме заказа, то можно рассчитать следующие характеристики работы магазина:

а) - min суточные затраты на складские операции;

б) - максимальный объем товарных запасов;

в) - величина цикла (период времени реализации всей заказанной партии товара);

г) - период времени завоза заказной партии товара
Недостатки полученной модели:

1. Рассматривается хранение товара только одной группы

2. Нет ограничений на емкость склада.

3. Существует равномерность спроса и завоза.
Так как формула (37) не учитывает собственную емкость склада, следует рассчитать необходимый объем складской емкости (Q*), который потребуется для хранения товарных запасов (max объем).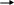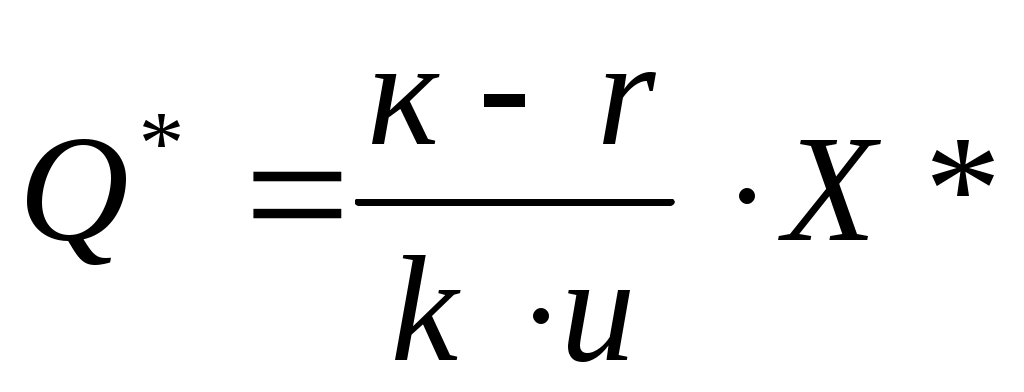


Сравним Q* с имеющейся в наличии емкостью склада Q.

–
Если Q* Q
собственной складской емкости достаточно и тогда заказ осуществляется в размере Х*, а экономические характеристики рассчитываются по формулам
а) - г).

-
Если Q*≥ Q
собственной складской емкости не хватает, в связи с чем, возникает задача по аренде дополнительных складских емкостей, либо об отказе от аренды.
Данная задача решается путем нахождения условного экстремума, где в качестве целевой функции выступает функция (36), а в качестве условия – ограничение на емкость склада.

Для решения этой задачи, применяется так называемый метод множителей Лагранжа.

Экономический смысл множителя Лагранжа  заключается в том, что он отражает предельную (мах) плату за аренду дополнительных складских емкостей, которую торговое предприятие в состоянии оплатить за аренду 1м³ складской емкости в сутки (при этом издержки на складские операции не увеличиваются):

(39)
Задания к лабораторному занятию

и самостоятельной работе студентов
В задаче оптимального управления товарными запасами известно следующее:

• 
  - объём склада;
  
• 
  - затраты на хранение 1 кг товара в сутки;
  
• 
  - затраты на завоз одной партии товара;
  
• 
  r(кг/сут) - равномерный спрос товара в сутки;
  
• 
  k (кг/сут) - равномерный темп поступления товара в сутки ( );
  
• 
  u (кг/м ) - удельная ёмкость склада;
  
• 
  α (руб./м³ * сут) - фактическая арендная плата.
  

Требуется:

1. 
   Определить объём заказываемой партии товара, при котором суммарные затраты на завоз и хранение минимальны.
   
2. 
   В случае необходимости решить, что выгоднее: уменьшить размер заказываемой партии товара или арендовать дополнительные складские ёмкости.
   
3. 
   Вычислить суточные издержки на завоз и хранение.
   

Методические указания к выполнению

Пункты 1, 2 задания выполняются по известной из лекций схеме:

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img108.gif" \* MERGEFORMAT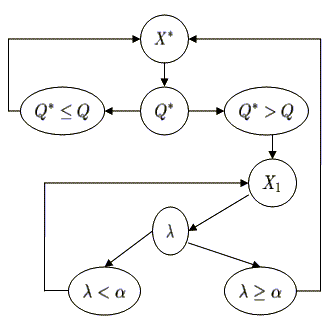

Рис. 1. Этапы решения задачи ОУТЗ
Обозначим через X’оптимальный объём заказываемой партии товара.

Из схемы ясно, что эта величина будет равна либо , либо 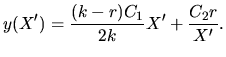. Тогда суточные издержки на складские операции вычисляются по формуле



Теоретические вопросы к самостоятельной работе студентов

1. 
   Постановка задачи оптимального управления товарными запасами.
   
2. 
   Этапы решения задачи оптимального управления товарными запасами.
   
3. 
   Оптимальный размер заказа партии товара.
   
4. 
   Экономический смысл множителя Лагранжа.
   
5. 
   В каком случае аренда дополнительного склада
   

а) выгодна? б) невыгодна?

Тема 6. Выборочный метод

Генеральная совокупность – это совокупность однородных объектов, изучаемая относительно некоторого показателя или группы показателей.

Количество объектов этой совокупности называют объемом генеральной совокупности (N).

Выборочная совокупность (выборка) – это совокупность, сформулированная случайным образом из объектов генеральной совокупности.

Количество объектов этой совокупности называется объемом выборки (n).

Объем генеральной совокупности очень велик и изучить его весь невозможно, а чаще и не целесообразно. С этой целью случайным образом из генеральной совокупности выбираются объекты.

Результаты исследования выборочной совокупности затем переносятся на генеральную совокупность с определенной степенью надежности.

В основе выборочного метода лежит закон больших чисел, суть которого заключается в том, что если объекты совокупности в отдельности ведут себя случайным образом, то в своей массе поведение всей совокупности объектов подчиняется определенным закономерностям.

Представительный объем выборки – это такой объем выборочной совокупности, который необходимо иметь в исследовании, чтобы с надежностью (вероятностью) P результаты исследования выборки можно было перенести на всю генеральную совокупность. Рассчитывается по формуле:

. (40)

где - допустимая относительная погрешность;

n_x – представительный объем выборки;

N – объем генеральной совокупности;

- выборочный коэффициент вариации;

t_p (n) - табличное значение, зависящее от объема выборки n и уровня надежности p.
Генеральная совокупность, а, следовательно, и выборочная совокупность, изучаются по характеристикам: среднее значение показателя (признака), выборочная средняя ( ),генеральной средней ( ), абсолютная погрешность приближения ( ), выборочное среднее квадратическое отклонение ( ) и др. (расчет этих показателей см. лекции).
Задания к лабораторному занятию и

самостоятельной работе студентов
Магазин собирается установить терминал для организации расчёта покупателей с помощью банковских карт. Было опрошено n человек, чтобы определить, какую сумму они истратили бы, рассчитываясь по пластиковым картам. Используя данные о предполагаемых расходах по банковским картам ( ), требуется:

• 
  оценить среднюю сумму возможных приобретений по банковской карте и построить для неё доверительный интервал с надёжностью ;
  
• 
  оценить уровень надёжности доверительного интервала, построенного при условии, что относительная погрешность не превышает;
  
• 
  определить представительный размер выборки, если администрации магазина хотелось бы оценить среднюю сумму приобретений по банковским картам с относительной погрешностью не более и уровнем надёжности .
  

Методические указания к выполнению

Дана выборка из n чисел: 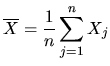. В первую очередь необходимо рассчитать выборочное среднее



и выборочную дисперсию

Построение доверительного интервала.

Пусть - среднее генеральной совокупности, которое требуется оценить. Все пункты задания выполняются на основании того, факта, что величина удовлетворяет t - распределению Стьюдента с m=n-1 степенями свободы. Следовательно, на основании таблицы t - распределения, приведённой в конце раздела, по заданному уровню надёжности можно отыскать число , для которого справедливо равенство



или

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img127.gif" \* MERGEFORMAT

(41)

Равенство (41) позволяет утверждать, что среднее генеральной совокупности , каковым бы оно ни было, лежит в интервале

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img128.gif" \* MERGEFORMAT

(42)

с вероятностью . Этот факт позволяет нам, не исследуя всю генеральную совокупность, делать довольно конкретные выводы о её характеристиках (в частности, о среднем).

Таким образом, ответом на пункт 1 задания является интервал (42), где величину t_α,m можно найти в таблице распределения Стьюдента, приведённой в конце раздела, на пересечении столбца и строки m.

Оценка уровня надёжности доверительного интервала

Сначала необходимо построить доверительный интервал, при условии, что относительная погрешность оценки среднего генеральной совокупности не превышает . Последнее означает, что абсолютная погрешность не превышает , что приводит к системе неравенств

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img134.gif" \* MERGEFORMAT

(43)

Приведя систему (43) к виду

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img135.gif" \* MERGEFORMAT

(44)

можно определить левую (A₁) и правую (A₂) границы для . Сделать это можно путём преобразований каждого из неравенств системы (43).

Теперь обратимся к равенству (41), в левой части которого также присутствуют левая и правая границы для . Остаётся только приравнять левые (или правые) границы для из (41) и (44):

INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img138.gif" \* MERGEFORMAT

(45)

Ещё раз поясним обозначения, используемые в равенстве (45):

• 
  A₁ - это левая граница доверительного интервала для при условии, что относительная погрешность оценки генерального среднего не превышает . Число A₁ уже должно быть вычислено в момент, когда вы получили систему неравенств вида (14).
  
• 
  , - также вычисленные величины на предыдущих этапах выполнения лабораторной работы.
  
• 
  Число n дано в исходных данных.
  

Таким образом, единственная неизвестная величина в уравнении (45) – это величина , где m=n-1, а - неизвестно. Не путайте величину с величиной , вычисленной на предыдущем этапе выполнения лабораторной работы и которую нашли из таблицы распределения Стьюдента по известным величинам и m. Поскольку в данном случае неизвестно, предстоит проделать в некотором роде обратную процедуру.

Так как в уравнении (45) все величины, кроме уже вычислены, можно выразить и вычислить (а также проверить ответ) величину . Теперь, зная, чему равно m, нужно обратиться к таблице распределения Стьюдента, а точнее - к строке, соответствующей числу m. В этой строке выбираем число, наиболее близкое к вычисленному вами значению . После того, как это число выбрано, оказывается, что оно находится в некотором столбце таблицы, соответствующем некоторому числу (смотри на заголовок столбца). Это и есть табличное значение .

Остаётся вычислить уровень надёжности построенного доверительного интервала (44). Им и будет значение вероятности, стоящей в правой части (41), то есть .
Определение представительного размера выборки

Для определения представительного размера выборки при заданных уровне надёжности и максимальной относительной погрешности необходимо проделать следующие шаги.

Во-первых, необходимо составить аналогичную системе (43) систему неравенств. Разница будет только в том, что вместо 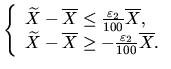нужно подставить . Получим:


Во-вторых, вновь получаем систему вида (44):

(46)
INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\labz\\img144.gif" \* MERGEFORMAT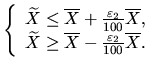

В третьих, приравниваем левую границу из последней системы неравенств (правая часть второго неравенства) к левой границе интервала (42) (с заменой 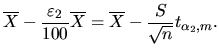на ):


Из последнего уравнения вычисляем n. Это и будет тот самый представительный размер выборки, необходимый для того, чтобы доверительный интервал (46) имел уровень надёжности .

Таблица 1

Таблица значений t-распределения Стьюдента

m
	0.80	0.40	0.20	0.10	0.05	0.02	0.01	0.001
1	0.325	1.376	3.078	6.314	12.706	31.821	63.657	636.619
2	0.289	1.061	1.886	2.920	4.303	6.965	9.925	31.598
3	0.277	0.978	1.638	2.353	3.182	4.541	5.841	12.941
4	0.271	0.941	1.533	2.132	2.776	3.747	4.604	8.610
5	0.267	0.920	1.476	2.015	2.571	3.365	4.032	6.869
6	0.265	0.906	1.440	1.943	2.447	3.143	3.707	5.959
7	0.263	0.896	1.415	1.895	2.365	2.998	3.499	5.405
8	0.262	0.889	1.397	1.860	2.306	2.896	3.355	5.041
Окончание табл. 1
9	0.261	0.883	1.383	1.833	2.262	2.821	3.250	4.781
10	0.260	0.879	1.372	1.812	2.228	2.764	3.169	4.587
11	0.260	0.876	1.363	1.796	2.201	2.718	3.106	4.437
12	0.259	0.873	1.356	1.782	2.179	2.681	3.055	4.318
13	0.259	0.870	1.350	1.771	2.160	2.650	3.012	4.221
14	0.258	0.868	1.345	1.761	2.145	2.624	2.977	4.140
15	0.258	0.866	1.341	1.753	2.131	2.602	2.947	4.073
16	0.258	0.865	1.337	1.746	2.120	2.583	2.921	4.015
17	0.257	0.863	1.333	1.740	2.110	2.567	2.898	3.965
18	0.257	0.862	1.330	1.734	2.101	2.552	2.878	3.922
19	0.257	0.861	1.328	1.729	2.093	2.539	2.861	3.883
20	0.257	0.860	1.325	2.725	2.086	2.528	2.845	3.850
21	0.257	0.859	1.323	1.721	2.080	2.518	2.831	3.819
22	0.256	0.858	1.321	1.717	2.074	2.508	2.819	3.792
23	0.256	0.858	1.319	1.714	2.069	2.500	2.807	3.767
24	0.256	0.857	1.318	1.711	2.064	2.492	2.797	3.745
25	0.256	0.856	1.316	1.708	2.060	2.485	2.787	3.725
26	0.256	0.856	1.315	1.706	2.056	2.479	2.779	3.707
27	0.256	0.855	1.314	1.703	2.052	2.473	2.771	3.690
28	0.256	0.855	1.313	1.701	2.048	2.467	2.763	3.674
29	0.256	0.854	1.311	1.699	2.045	2.462	2.756	3.659
30	0.256	0.854	1.310	1.697	2.042	2.457	2.750	3.646
40	0.255	0.851	1.303	1.684	2.021	2.423	2.704	3.551
60	0.254	0.848	1.296	1.671	2.000	2.390	2.660	3.460

Значение находится на пересечении строки m и столбца α.

Теоретические вопросы к самостоятельной работе студента

1. 
   Понятие генеральной и выборочной совокупности.
   
2. 
   Почему при формировании выборочной совокупности необходимо использовать только случайный отбор?
   
3. 
   Суть закона больших чисел.
   
4. 
   Среднее квадратическое отклонение.
   
5. 
   Коэффициент вариации.
   
6. 
   Абсолютная погрешность выборки.
   
7. 
   Относительная погрешность выборки.
   
8. 
   Доверительный интервал.
   
9. 
   Представительный размер выборки.