Главная страница
Навигация по странице:

  • Задания к лабораторному занятию

  • Методические указания к выполнению

  • Теоретические вопросы к самостоятельной работе студентов

    		•

    методЭММ 21.06.2010. Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10


    Скачать 0.98 Mb.
    НазваниеМетодические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10
    Дата08.04.2022
    Размер0.98 Mb.
    Формат файлаdoc
    Имя файламетодЭММ 21.06.2010.doc
    ТипМетодические указания
    #454216
    страница4 из 7
    1   2   3   4   5   6   7

    Тема 4. Системы массового обслуживания (СМО)



    Различают три вида СМО:

    1. Система с отказом - это такая система, что в случае ее занятости обслуживанием требований, вновь поступающие требования не обслуживаются.

    2. Система с очередью - это такая система, что в случае ее занятости обслуживанием требований, вновь поступающие становятся в общую очередь на обслуживание.

    3. Система смешанного типа - это такая система, которая имеет ограниченную длину очереди и вновь поступающие требования, превышающие фиксированную длину очереди, не обслуживаются.

    Рассмотрим систему с очередью.

    Система с очередью характеризуется следующими показателями:

    Число  называется интенсивностью входящего потока и показывает, сколько в среднем требований поступает на обслуживание в единицу времени.

    Число  называется интенсивностью обслуживания и показывает, сколько в среднем требований обслуживается одним каналом в единицу времени.

    Параметр загрузки α показывает, сколько в среднем
    каналов занято обслуживанием требований. Это безразмерная величина.
    ( 29)
    Чтобы система была с очередью необходимо выполнение так называемого условия стационарности:

    (30)

    .

    Оно заключается в следующем: чтобы система была с очередью, интенсивность входящего потока должна быть меньше интенсивности обслуживания требований всей системой.

    Наряду с этим, можно пользоваться и модификацией условия стационарности:

    .

    Она получается делением обеих частей неравенства на величину ( ), т.к. , то .

    То есть, чтобы система была с очередью, необходимо чтобы среднее число каналов, занятых обслуживанием, было меньше фактического числа каналов. В противном случае очередь будет неограниченно расти и, в итоге, СМО с очередью перейдет в систему с отказом.

    При сформулированных условиях можно рассчитать следующие показатели работы для двухканальной системы:
    - доля времени простоя всей системы

    (не занят обслуживанием ни один канал);

    - доля времени занятости одного канала (1 или 2);

    - доля времени занятости обоих каналов.

    - средняя доля времени простоя.

    - средняя длина очереди.
    Задания к лабораторному занятию

    и самостоятельной работе студентов


    1. В магазине к узлу расчета, состоящему из двух касс, поступает поток покупателей с интенсивностью человек в минуту; , интенсивности обслуживания покупателей первой и второй кассой соответственно. Определить:

    • параметр загрузки системы;

    • долю времени простоя обеих касс одновременно;

    • долю времени работы одной кассы;

    • долю времени работы обеих касс одновременно;

    • среднюю долю времени простоя системы;

    • среднюю длину очереди;

    1. Используя информацию об интервалах времени между поступлениями покупателей в узел расчёта и времени, затрачиваемом первым и вторым кассирами на обслуживание, требуется построить таблицу распределения покупателей при следующих предположениях:

    • если обе кассы свободны, покупатель обслуживается первой кассой;

    • если обе кассы заняты, то покупатель становится в общую очередь и обслуживается той кассой, которая освободилась.

    Вычислить:

    • среднее время ожидания покупателя в очереди;

    • долю времени простоя и долю времени работы обеих касс;

    • долю времени работы каждой из касс;

    • долю времени простоя каждой из касс.



    Методические указания к выполнению
    В исходных данных в том числе даны три числа: интенсивность входящего потока, интенсивность обслуживания первой кассы и интенсивность обслуживания второй кассы .

    Параметр загрузки системы вычисляется по формуле:



    где - средняя интенсивность обслуживания одной кассы.

    Остальные характеристики системы массового обслуживания , которые требуется найти в пункте 1, считаются по формулам, имеющимся на стр. 26 и в лекциях.


    Имитационное моделирование работы СМО



    В исходных данных дана таблица со следующими показателями:

    • интервалы между поступлениями покупателей на узел расчёта;

    • время обслуживания первой кассой t1;

    • время обслуживания второй кассой t2.

    Для выполнения задания 2 необходимо построить таблицу из 7 строк и 16 столбцов следующего вида:


    Номер покупателя

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16

    Время поступления покупателя

     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

    Время ожидания

     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

    Время обслуживания первой кассой

     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

    Время окончания обслуживания первой кассой

     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

    Время обслуживания второй кассой

     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

    Время окончания обслуживания второй кассой

     
     
     
     
     
     
     
     
     
     
     
     
     
     
     
     

    Пример заполнения таблицы см. в лекциях.

    Первый покупатель всегда приходит в момент 0, т.е., 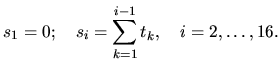. Второй покупатель приходит через время после первого, т.е. . Третий покупатель приходит через время после второго, т.е., и так далее. Общая формула для значений второй строки таблицы выглядит следующим образом:



    Далее таблица заполняется по столбцам. Рассмотрим небольшой пример. Пусть исходные данные выглядят следующим образом:

    :
    5
    12
    3
    7
    ...

    ti 1:
    5
    16
    7
    20
    ...

    ti 2:
    8
    44
    10
    6
    ...

    Первый покупатель идет в первую кассу (см. условия пункта 2 задания), его обслуживание начинается в момент 0 и заканчивается в момент 5. Второй покупатель подходит в момент 5 и обслуживается первой кассой, так как она уже свободна. Третий покупатель, поскольку первая касса занята, обслуживается второй кассой. Четвертый покупатель встанет в общую очередь (обе кассы заняты), и после ожидания в течение 1-ой единицы времени будет обслуживаться в первой кассе, т.к. она освободится раньше. И так далее, смотрите таблицу ниже.

    i:
    1
    2
    3
    4
    ...

    si:
    0
    5
    17
    20
    ...

    wi:
    0
    0
    0
    21-20=1
    ...

    :
    5
    16



    7
    ...

    :
    0+5=5
    5+16=21



    20+1+7=28
    ...

    :






    8



    ...

    :






    17+8=25



    ...

    Итак, будем считать, что таблица заполнена. Это означает, что вы располагаете числами

    Если какая-либо клетка в таблице пуста, то значение, соответствующее этой клетке полагается равным нулю.

    Для расчёта характеристик, которые требуется рассчитать в пункте 2 задания, необходимо следующее:

    1. Вычислить величины

    1. - суммарное время ожидания;

    2. - чистое время работы 1-ой кассы;

    3. - время окончания обслуживания последнего покупателя на 1-ой кассе;

    4. - чистое время работы 2-ой кассы;

    5. - время окончания обслуживания последнего покупателя на 2-ой кассе.

    1. На основе рассчитанных выше величин, рассчитываются следующие показатели:

    1. - среднее время ожидания покупателя в очереди;

    2. - средняя доля времени простоя касс;

    3. - средняя доля времени работы касс;

    4. - средняя доля времени работы 1-ой кассы;

    5. - средняя доля времени работы 2-ой касс;

    6. - средняя доля времени простоя 1-ой кассы;

    7. - средняя доля времени простоя 2-ой кассы

    Теоретические вопросы к самостоятельной работе студентов


    1. Система массового обслуживания (СМО). Виды систем массового обслуживания.

    2. Интенсивность входящего потока.

    3. Интенсивность обслуживания.

    4. Параметр загрузки системы: формула и экономический смысл.

    5. Условие стационарности.

    6. Характеристики работы двухканальной СМО с очередью: формулы и экономический смысл.

    7. Контрольное правило.
    1   2   3   4   5   6   7

    написать администратору сайта