методЭММ 21.06.2010. Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10
 Скачать 0.98 Mb.
|
|
СИБИРСКИЙ УНИВЕРСИТЕТ ПОТРЕБИТЕЛЬСКОЙ КООПЕРАЦИИ ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 2010Кафедра статистики и экономического прогнозирования Экономико-математические методы. Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов / под ред. д-ра экон. наук, проф. Н. В. Шаланова.– Новосибирск: СибУПК, 2010. – 51с. Авторы: д-р экон. наук, проф. Шаланов Н. В. ст. преподаватель Иванова Т. М. ассистент Чернавина С. В. Рецензент: д-р экон. наук, проф. Т. Г. Храмцова Методические указания и задания к лабораторным занятиям и самостоятельной работе утверждены и рекомендованы к изданию кафедрой статистики и экономического прогнозирования, протокол от 28.08.2009 № 1 © Сибирский университет потребительской кооперации, 2010 СОДЕРЖАНИЕ
ВВЕДЕНИеЭкономико-математическое моделирование экономических процессов в настоящее время стало одним из важных направлений развития экономической теории и совершенствования управления этими процессами. Торговля, как одна из важнейших отраслей социальной инфраструктуры, нацеленная на удовлетворение населения в товарах и поддержание нормальных условий его жизнедеятельности, также нуждается в более глубоком и всестороннем изучении, что невозможно осуществить без применения методов количественного анализа, модельного аппарата, способного адекватно отразить существующее состояние и дать достоверный прогноз перспектив развития. Изучение дисциплины «Экономико-математические методы» основано на использовании знаний, полученных студентами в ходе освоения других дисциплин – «Экономика», «Статистика», «Информатика». Так как практические занятия по дисциплине проводятся на компьютере, студент должен иметь элементарные знания и навыки работы в операционной системе WINDOWS и основные функции программы Microsoft Excel, что позволит экономить учебное время студентов и дает им возможность максимально сосредоточиться на освоении экономико-математических методов. В результате изучения дисциплины «Экономико-математические методы» студент должен: иметь представление об основных понятиях и принципах экономико-математического моделирования; знать основные математические модели и методы, применяемые в исследовании деятельности торговых организаций; уметь производить расчеты профессионально ориентированных задач на основе изучаемых методов. Все задания выполняются студентами применительно к своему варианту. Часть из представленных заданий предназначены как для работы в аудитории, так и самостоятельной работы студентов. Самостоятельная часть заданий выполняется студентами по материалам лекций. Исходные данные для выполнения лабораторных заданий представлены в программе «Экономико-математические методы и модели», находящейся на рабочем столе любого компьютера учебных аудиторий СибУПК. Задания студентами выполняются в MS Excel, а результаты проверяются самой программой «Экономико-математические методы и модели». Краткое руководство по работе с программой при выборе персонального задания и его выполнении: Открыть программу «Экономико-математические методы и модели» двойным щелчком мыши по ярлыку программы. Щелкнуть кнопкой мыши на надпись в конце листа программы исходные данные и проверка ответов. Пройти регистрацию, нажав на надпись вверху страницы программы «Регистрация». В листе «Регистрация» внести свои персональные данные; по окончании заполнения листа, нажать кнопку «Зарегистрировать». Для выбора персонального варианта заданий осуществить «Вход» (нажав на аналогичную надпись «Вход»), введя в соответствующие поля программы данные, внесенные в лист регистрации: имя пользователя и пароль. Эти данные необходимо будет вводить каждый раз при входе в программу и выборе персонального задания по теме. Далее необходимо следовать ссылкам, появляющимся на листах программы. Для получения исходных данных выбрать тему в предлагаемом перечне программы, нажать кнопку «Выбрать», нажать на появившуюся после загрузки ссылку, нажать на появившемся листе кнопку «Получить другие числа», нажать ОК. Получив данные, соответствующие зарегистрированному персональному варианту, скопировать их и вставить в файл, созданный в MS Excel. Сохранить файл на диск Z. Здесь же в этом файле должны выполняться все расчеты показателей, указанных в задании. Все расчеты рекомендуется выполнять на одном листе для упрощения взаимосвязи формул. Вернуться в программу, где представлены исходные данные и нажать внизу листа кнопку «Проверить ответы». На этот лист вставляются рассчитанные в MS Excel показатели и проверяются. Если значение рассчитано правильно – программа выдаст напротив него резюме «Верно», если значение рассчитано не верно – появится резюме «Ошибка». Работа студента осуществляется в двух окнах программ: 1) расчеты показателей в файле MS Excel, 2) лист «Проверка ответов» в программе «Экономико-математические методы и модели». При единовременном заполнении всех показателей по конкретно выбранной теме на листе «Проверка ответов» и получении всех ответов «Верно», зачет по данной теме заносится самой программой в общую базу списка студентов СибУПК. Количество выполненных работ можно посмотреть, зайдя на лист «Результаты» и осуществив поиск по листу: Правка – Найти на этой странице – в появившемся диалоговом окне в поле набрать искомую фамилию и имя. Цифра «1» напротив темы означает, что работа выполнена, «0» - работа не выполнена. МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ К ЛАБОРАТОРНЫМ ЗАНЯТИЯМ И САМОСТОЯТЕЛЬНОЙ РАБОТЕ СТУДЕНТОВ Тема 1. Производственные функции Производственная функция – это функция, описывающая соотношение между производственными ресурсами и объемом выпускаемой продукции. Производственная функция в общем виде:  , или  (1)где у – объемом выпускаемой продукции;  (x1, x2, ..., xn) – вектор производственных ресурсов. Основные свойства ПФ: 1. Если какой-либо из используемых производственных ресурсов отсутствует, то производство продукции невозможно, т.е. если xi = 0, то f  = 0.2. При увеличении объемов используемых ресурсов объем выпускаемой продукции возрастает (функция монотонно возрастающая). Для оценки эффективности использования производственных ресурсов применяются следующие количественные показатели: 1. Величина  называется предельной эффективностью использования i-го ресурса и показывает, на сколько увеличится объем выпускаемой продукции при увеличении i-го производственного ресурса на единицу. Т.е. характеризует прирост выпуска продукции при приросте i-го производственного ресурса на единицу. 2. Величина  называется средней эффективностьюиспользования i-го ресурса и показывает, какое количество выпускаемой продукции приходится на единицу i-го ресурса. 3. Величина  называется эластичностью использования i-го ресурса (выпуска продукции по отношению к затратам i-го ресурса) и показывает, насколько % увеличится объем выпускаемой продукции при увеличении затрат данного ресурса на 1%. Множество сочетаний объемов используемых ресурсов, при которых выпускается один и тот же объем продукции, называется изоквантой. Определим изокванту для производственного процесса, представленного степенной функцией типа  .Пусть y0 – фиксированный объем выпускаемой продукции. Тогда изокванта внеявной форме будет иметь вид  (2)Из данного уравнения, выразив x2 через x1, найдем изокванту в явном форме  (3)Графически изокванту для производственной функции данного типа можно представить в виде следующего рисунка - гиперболы:  Экономическая область - это все то множество сочетаний объемов используемых ресурсов, при котором производственная функция адекватно (реалистично) описывает производственный процесс.  Задания к лабораторному занятию и самостоятельной работе студентов Даны показатели работы торговой организации за пять лет с 2002 по 2006 гг.: товарооборот у, численность работников x1 и площадь торгового зала x2. В следующем году планируется увеличить товарооборот на 20% по отношению к 2006 г. Построить изокванту, соответствующей планируемому товарообороту, то есть определить, при каких сочетаниях количества работников и площади торгового зала возможно такое увеличение товарооборота, при условии, что на одного работника может приходиться от 10 м2 до 50 м2 торговой площади. Методические указания к выполнению Создайте новый файл в Microsoft Excel и скопируйте из программы «Экономико-математические методы» в этот файл исходную таблицу данных, которую в дальнейшем будем называть таблицей 1. 2. Взаимосвязь товарооборота у, численности работников х1 и площади торгового зала х2 описывается производственной функцией вида  (4)где  - числовые параметры. Чтобы найти численность работников х1 и площадь торгового зала х2, сначала необходимо рассчитать параметры функции . Для этого данную степенную функцию приводимк линейному виду путем логарифмирования обеих частей уравнения ,так как логарифм произведения равен сумме логарифмов, то  .Используя свойство логарифма степени, получим:  .В соответствии с этим, необходимо прологарифмировать данные таблицы 1, и результаты занести в таблицу 2 (рис. 1). Таблица 2. Натуральные логарифмы исходных данных Таблица 1. Исходные данные  
Рис. 1. Пример оформления работы при нахождении Ln Для этого выполните следующие действия: поставьте курсор в ячейку «ln y» за 2002 год; выполните команды ВСТАВКА  ФУНКЦИЯ МАТЕМАТИЧЕСКИЕ LN; выделите значение товарооборота за 2002 год и нажмите ОК; ячейку с получившимся числом растяните на 2 столбца вправо, а затем на 4 столбца вниз, потянув мышью за маленький чёрный квадратик в правом нижнем углу ячейки. На основании данных натуральных логарифмов, рассчитайте параметры функции с помощью функции Регрессия. Выполните команды СЕРВИС АНАЛИЗ ДАННЫХ РЕГРЕССИЯ. В полученном окне (рис. 2) введите «Входной интервал Y» и «Входной интервал X». Чтобы заполнить поле «Входной интервал Y», поместите в это поле курсор и выделите левой кнопкой мыши столбец таблицы 2 «lny», соответствующий товарообороту. Для заполнения поля «Входной интервал X», выделите два столбца таблицы 2 ln x1 и ln x2, соответствующие численности работников и площади торгового зала. Ничего больше в диалоге РЕГРЕССИЯ не изменяйте. После заполнения входных интервалов нажмите ОК. INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\методические указания\\labz\\img12.gif" \* MERGEFORMAT 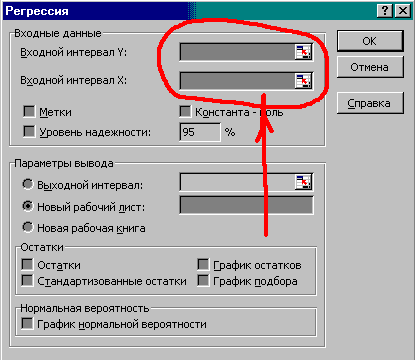 Рис. 2. Диалоговое окно функции Регрессия Результаты Регрессии буду представлены на отдельном новом листе вашего файла MS Excel аналогично рис. 3. Скопируйте эти результаты и поместите их на лист 1, где расположены исходные данные. INCLUDEPICTURE "\\\\vsupk\\groups\\Кафедра статистики и математики\\Все документы кафедры\\методические указания\\labz\\img13.gif" \* MERGEFORMAT 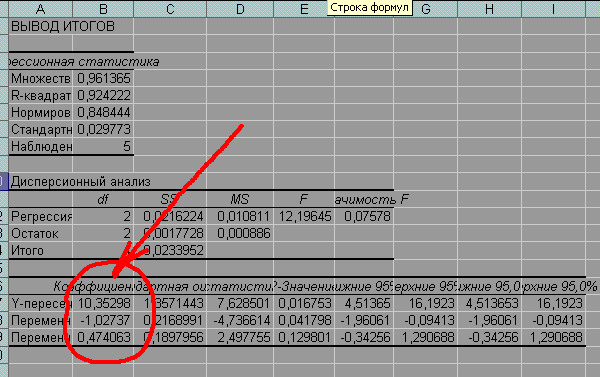 Рис. 3. Результаты функции «Регрессия» На рис. 3 выделены три числа. Сверху вниз это:  , где  . Коэффициенты  найдены сразу же. Из последнего равенства рассчитайте  Чтобы найти  , выполните действия: выделите свободную ячейку в MS Excel; выполните команды ВСТАВКА ФУНКЦИЯ МАТЕМАТИЧЕСКИЕ EXP;отодвиньте (недалеко) с помощью мыши возникшее окно в сторону и выделите значение  (верхнее из трёх чисел на рисунке); нажмите ОК. Так вы получите коэффициент α. Итак, коэффициенты производственной функции, заданной уравнением (1), найдены. 1Нахождение изокванты и граничных значений ресурсов.Найти минимальные и максимальные значения используемых ресурсов (численности работников и торговой площади) при условии, что товарооборот увеличился на 20 % по сравнению с 2006 г. нужно решив две системы уравнений:   (5)  (6)Величина  в системах (5), (6) соответствует значению товарооборота за 2006 г., увеличенному на 20%.Решение системы (5) соответствует максимальной численности работников и минимальной торговой площади, а решение системы (6) - минимальной численности работников и максимальной торговой площади. Теоретические вопросы к самостоятельной работе студентов Производственная функция: сущность, общий вид записи. Свойства производственной функции. Предельная эффективность использования ресурса. Средняя эффективность использования ресурса. Эластичность использования ресурса. Экономическая область. Понятие изокванты. Изокванта в явном и неявном виде. Графическое изображение изокванты для каждого вида производственной функции. |