методЭММ 21.06.2010. Методические указания и задания к лабораторным занятиям и самостоятельной работе студентов всех специальностей Новосибирск 20 10
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
Тема 3. Межотраслевой балансСуществуют два вида МОБ: натуральный и стоимостный. Рассмотрим модель натурального МОБ. Учитывая, что валовая продукция распадается на промежуточную и конечную, имеет место для каждой модели балансовое уравнение(для i-й отрасли): где Zi - промежуточная продукция, идущая на производственное потребление (т.е. потребляется самой отраслью и другими отраслями сферы материального производства); yi - конечная продукция, идущая на непроизводственное потребление (личное потребление и потребление отраслями непроизводственной сферы – культура, спорт и др.). Однако этот баланс не учитывает межотраслевой специфики промежуточной продукции. Для устранения этого недостатка введем следующее обозначение промежуточной продукции: xij - объем продукции произведенной i-й отраслью и переданный и j-й отрасли для дальнейшего производства. На основании этого можно составить систему балансовых уравнений, охватывающих всё n-количество отраслей производственной сферы:  Преобразуем эту систему (разделив и умножив промежуточные продукции отраслей на соответствующие валовые продукции потребляющих отраслей): 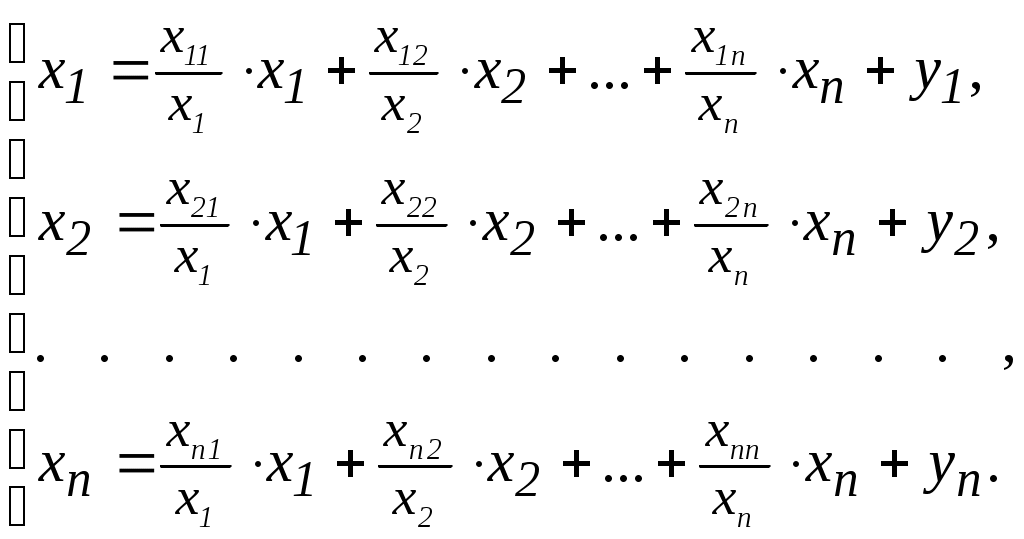 Введем такое понятие, как коэффициент прямых затрат. Он показывает, сколько валовой продукции i-я отрасль должна передать j-ой отрасли, чтобы последняя произвела единицу своей валовой продукции: Учитывая это, последняя система уравнений примет вид: 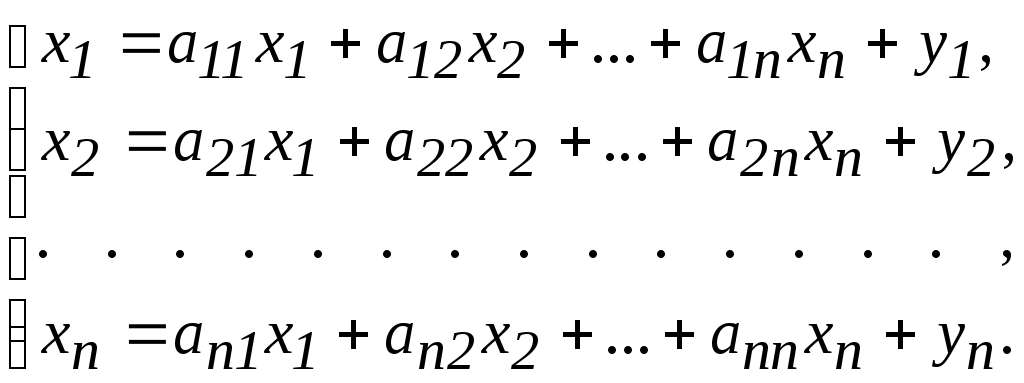 Перейдем к матричной форме МОБ, введя следующие обозначения: 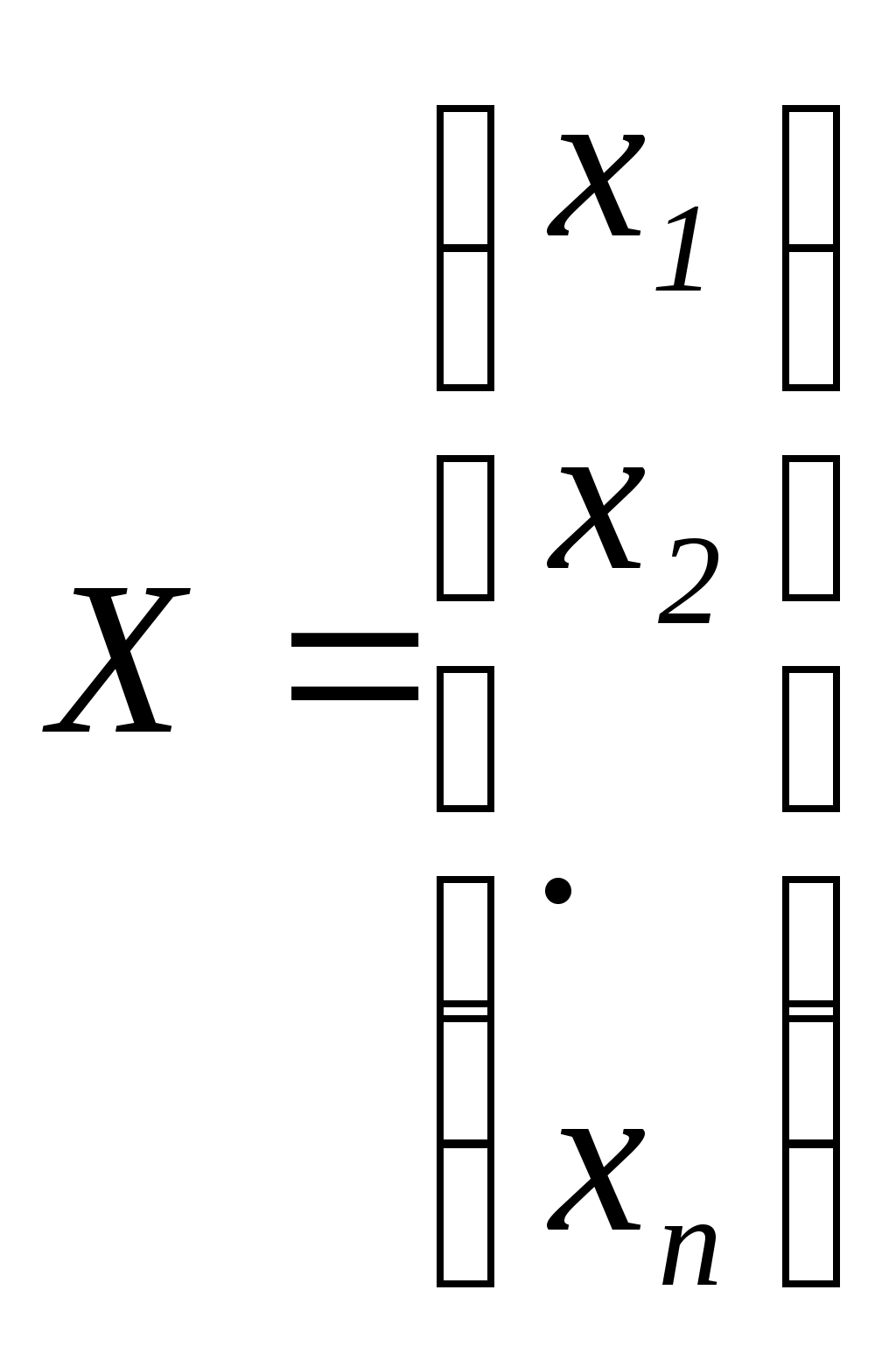 - вектор-столбец валовой продукции отраслей - вектор-столбец валовой продукции отраслей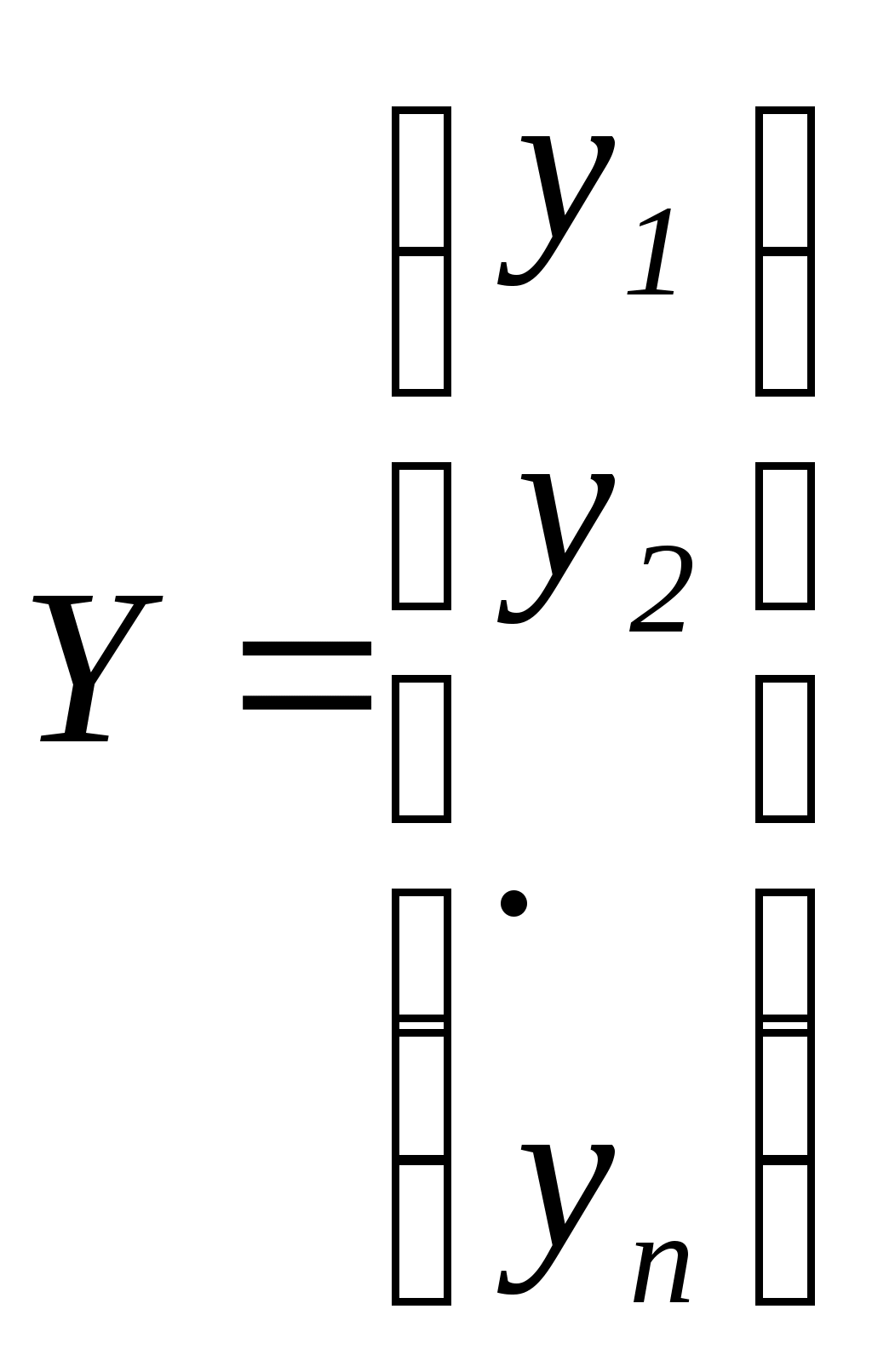 - вектор-столбец конечной продукции отраслей - вектор-столбец конечной продукции отраслей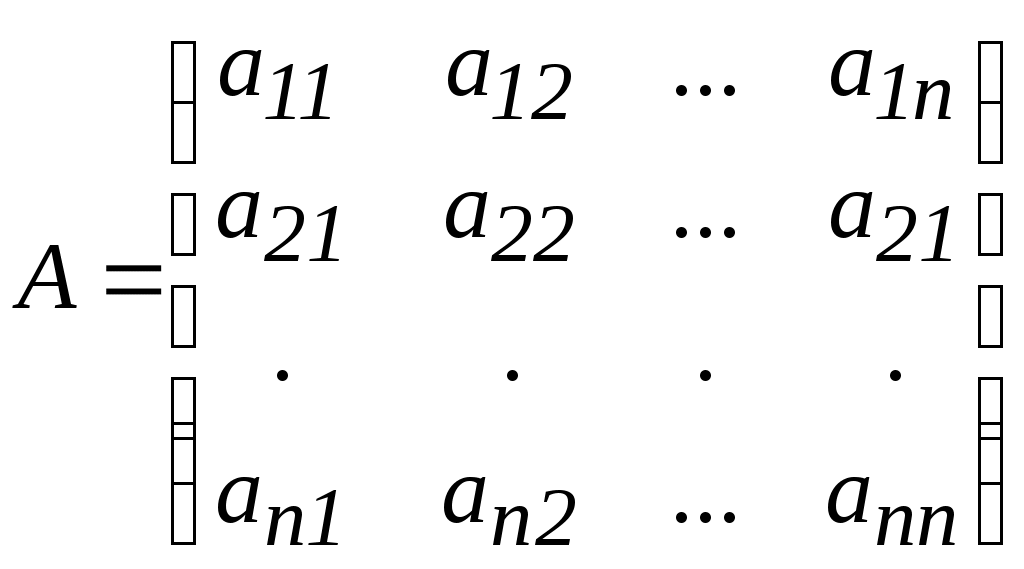 - матрица коэффициентов прямых затрат. - матрица коэффициентов прямых затрат.Отсюда матричная модель МОБ примет вид: X = AX + Y С помощью модели МОБ решаются 2 задачи: 1. Определение объемов конечной продукции по известным объемам валовой продукции отраслей: Y = (E – A)X 2. Определение объемов валовой продукции по известным объемам конечной продукции отраслей: X = (E - A) -1Y Матрица (E - A)-1называется матрицей коэффициентов полных затрат. Она показывает, сколько валовой продукции i-я отрасль должна передать j-й отрасли, чтобы j-я отрасль произвела единицу своей конечной продукции. Задания к лабораторному занятию и самостоятельной работе студентов Пусть народное хозяйство состоит из трёх отраслей. По данным отчётного периода составлен его баланс между Определить на следующий период: матрицу коэффициентов прямых затрат; матрицу коэффициентов полных затрат; валовую продукцию каждой отрасли. Методические указания к выполнению Скопируйте исходные данные в Ms Excel. В качестве исходных данных даны значения Нахождение матрицы коэффициентов прямых затратДля расчета коэффициентов прямых затрат определяется валовая продукция каждой отрасли за текущий период Теперь вычисляются 9 коэффициентов прямых затрат: где Нахождение матрицы коэффициентов полных затрат осуществляется в два этапа. Сначала необходимо вычислить матрицу |

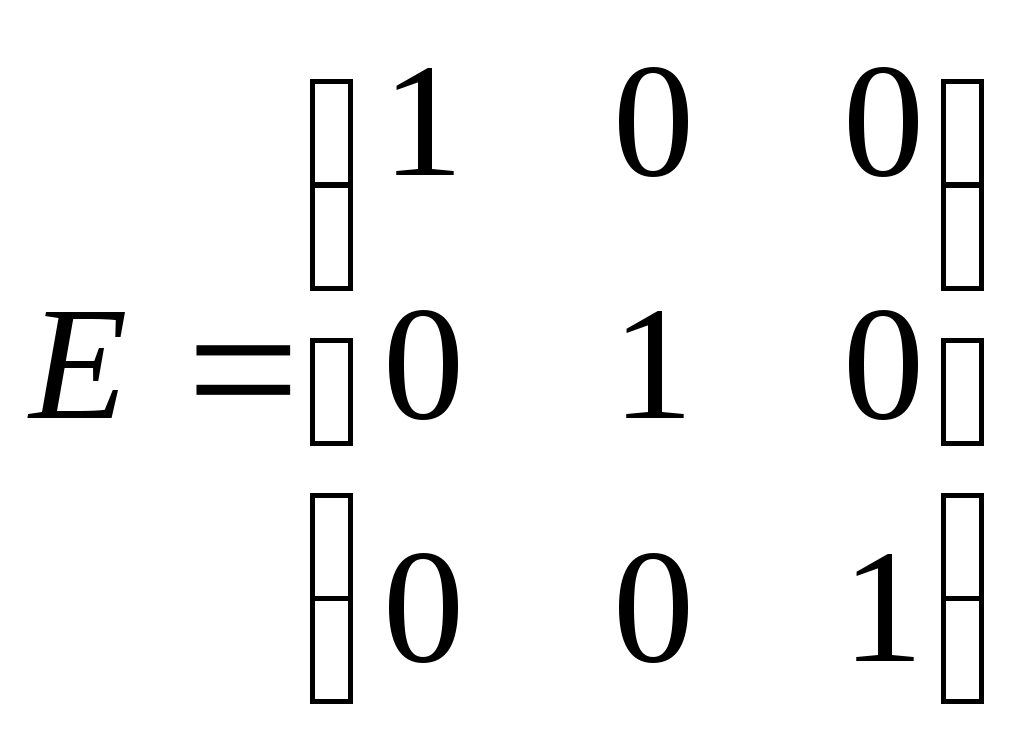 (26)
(26)