Эконометрика. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе
 Скачать 202.39 Kb. Скачать 202.39 Kb.
|
РешениеПервых два примера являются примерами количественных показателей, т.к. они заданы с помощью числовых значений (34 года и 8,1%). Последний пример – это качественный показатель, мы просто говорим, что состояние критическое, не приводя никаких числовых значений. Задача 3. Определите в приведенных ниже парах показателей результирующую и объясняющую переменные: а) товарооборот магазина и численность его работников; б) стоимость квартиры и ее общая площадь. Решение В первой паре показателей результирующей переменной является товарооборот магазина, так как он является результатом его деятельности, а объясняющей переменной является численность работников, от которой зависит товарооборот магазина. Во второй паре показателей результирующей переменной является стоимость квартиры, так как полностью зависит от фактора – общаяплощадь квартиры. В соответствие с этим, общая площадь квартиры является объясняющей переменной. Тема 2. Информационные технологии эконометрических исследований Современный бизнес невозможен без информационной поддержки, применения информационных систем и информационных технологий. Любой фирме требуется своевременный и тщательный анализ имеющейся информации и получение из нее надежных и обоснованных выводов и прогнозов. Поэтому потребность в средствах статистического и эконометрического анализа данных очень велика, что и послужило причиной развития рынка статистических и эконометрических программ, на котором предлагается большое количество информационных статистических систем. В эконометрике для проведения расчетов часто используют табличный процессор MicrosoftExcel. С помощью функций MicrosoftExcelможно рассчитать коэффициент корреляции с помощью статистической функции «КОРРЕЛ». С помощью функций MicrosoftExcelможно определить параметры однофакторных и многофакторных линейных и нелинейных функций. Однако нелинейные функции сначала необходимо привести к линейному виду. Существует несколько способов определения параметров уравнений регрессий: С помощью статистических функций «ОТРЕЗОК» и «НАКЛОН». Функция «Наклон» служит для определения параметра b уравнения регрессии, а функция «Отрезок» – для определения свободного члена уравнения – а. С помощью статистической функции «Линейн». Практически все эконометрические модели можно идентифицировать с помощью этой функции. Результаты использования этой функции получаем в виде следующей таблицы: Результаты регрессионного анализа
Для нахождения параметров показательной парной регрессии (не приводя ее к линейному виду) можно использовать статистическую функцию «ЛГРФПРИБЛ». Основные этапы и результаты ее построенияаналогичны функции «Линейн». С помощью статистического пакета «Анализ данных» - «Регрессия», который позволяет определить коэффициенты корреляции и детерминации, фактическое значение критерия Фишера, параметры уравнения регрессии и другие показатели. Для приведения нелинейных уравнений к линейному виду могут использоваться Математические функции, такие как «LN» и «EXP». При построении множественной регрессии для построения матрицы парных и частных коэффициентов корреляции используют статистический пакет «Анализ данных» «Корреляция». В настоящее время разработано много специализированных эконометрических пакетов для построения и анализа эконометрических моделей. Назовемнекоторыеизних: Stata; EViews; Gauss; SPSS; PcGive;STATISTICA;Minitab; STADIA;Mathcad;STATGRAPHICS;S-plus;ForecastExpert; ЭВРИСТА; МИЗОЗАВР; ОЛИМП: Стат-Эксперти другие. Тема 4. Парная регрессионная модель Парная (простая, однофакторная) регрессия – регрессия, в которой рассматривается зависимость показателя Y от одного фактора Х. В общем виде эту зависимость можно задать функцией: 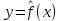 где у – зависимая переменная (результативная переменная) х – независимая или объясняющая переменная (фактор-признак) На практике наиболее широко используется линейная парная регрессия 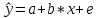 . .Коэффициент a – отрезок; формально – это значение результативной переменной при x=0. Если фактор-признак не имеет и не может иметь нулевого значения, то интерпретацияа не имеет смысла. Интерпретировать можно лишь знак при параметре а. Еслиа>0, то относительное изменение результата происходит медленнее, чем изменение фактора. Другими словами, вариация результата меньше вариации фактора-признака. Приа<0 – интерпретация вообще смысла не имеет. Коэффициент b – наклон, показывает среднее изменение результата при изменении фактора на единицу. Например, зависимость стоимости квартиры (тыс.руб.) от общей площади квартиры (кв.м.) задается уравнением регрессии  =145+13,3x, тогда можно сделать вывод, что при увеличении общей площади квартиры на 1 кв.м. ее стоимость возрастает на 13,3 тыс.руб. =145+13,3x, тогда можно сделать вывод, что при увеличении общей площади квартиры на 1 кв.м. ее стоимость возрастает на 13,3 тыс.руб.Регрессионное уравнение  = a+bx указывает, что при увеличении фактора х на единицу Y увеличивается на b единиц, приb>0. = a+bx указывает, что при увеличении фактора х на единицу Y увеличивается на b единиц, приb>0.Регрессионное уравнение 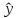 = a–bx указывает, что при увеличении фактора х на единицуY уменьшается на b единиц, при b<0. = a–bx указывает, что при увеличении фактора х на единицуY уменьшается на b единиц, при b<0.После того, как найдено уравнение однофакторной регрессии необходимо оценить его качество. Для оценки качества подбора линейной функции используют следующие показатели: Коэффициент детерминации. Он рассчитывается возведением в квадрат линейного коэффициента корреляции (r2xy). Он показывает, на сколько процентов вариация фактора х объясняет вариацию результативного показателя у. Средняя ошибка аппроксимации–это среднее отклонение расчетных значений 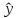 от фактических у. от фактических у.О 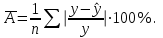 на вычисляется по формуле: Допустимый предел значений средней ошибки аппроксимации не более 8-10%. Если А< 8%, то ошибка аппроксимации небольшая, и регрессионная модель хорошо описывает изучаемую закономерность. Если 8% 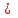 А А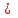 10%, ошибка аппроксимации высокая, но регрессионная модель хорошо описывает изучаемую закономерность. 10%, ошибка аппроксимации высокая, но регрессионная модель хорошо описывает изучаемую закономерность. Если А>10% , ошибка аппроксимации высокая, но регрессионная модель плохо описывает изучаемую закономерность. F- критерий Фишера. F – тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Сравниваются фактическое Fфакт и критическое (табличное) Fтабл значения F- критерий Фишера. F 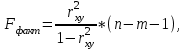 факт можно рассчитать по формуле: где n – число единиц совокупности; m – число факторов, включаемых в модель. Fтабл– этомаксимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости . Уровень значимости – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно принимается равной 0,05 или 0,01. (Будем при решении задач принимать =0,05.) При нахождении Fтаблв таблице значений F-критерия Фишера будем принимать: k1 = m и k2 = n-2 , где n – объем выборки, m – количество объясняющих переменных. Гипотеза Н0 – природа оцениваемых характеристик случайна. Гипотеза Н1 – природа оцениваемых характеристик не случайна. Если Fтабл Если Fтабл>Fфакт, то Н0 – гипотеза о случайной природе оцениваемых характеристик не отклоняется и признается их статистическая незначимость и ненадежность с вероятностью 1-. Таким образом, качество модели считается высоким, если выполняются все три условия: коэффициент детерминации 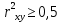 ; ;средняя ошибка аппроксимации 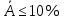 ; ;Fтабл Если хоть одно из условий не выполняется, качество модели низкое.Выбор наилучшего варианта эконометрической модели осуществляется сравнением их качественных характеристик. Соответственно лучшему варианту модели должны соответствовать лучшие характеристики. Образец решения задачи контрольной работы: По Российской Федерации за 2009 год известны значения двух признаков (табл. 3.1). Таблица 3.1
Для оценки зависимости Y от Х построена парная линейная регрессионная модель с помощью метода наименьших квадратов 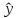 = а + bх + е, где а = = а + bх + е, где а = 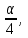 b = b = 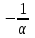 . Парный коэффициент корреляции rxy= . Парный коэффициент корреляции rxy=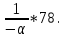 Средняя ошибка аппроксимации Средняя ошибка аппроксимации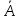 = = 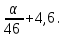 Известно, что Fтабл= 4,96, а Fфакт = Известно, что Fтабл= 4,96, а Fфакт = 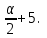 Определите коэффициент детерминации. Оцените линейную модель через среднюю ошибку аппроксимации и F-критерий Фишера. Определите коэффициент детерминации. Оцените линейную модель через среднюю ошибку аппроксимации и F-критерий Фишера.Решение. Пусть, например, число 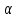 =302. Тогда найдем коэффициенты парной линейной регрессионной моделиа= 75,5 и b= -0,003. Получили уравнение регрессии: =302. Тогда найдем коэффициенты парной линейной регрессионной моделиа= 75,5 и b= -0,003. Получили уравнение регрессии: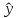 = 75,5-0,003х+е. = 75,5-0,003х+е.Значит, с увеличением среднего денежного дохода на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,003 процентных пункта. Линейный коэффициент парной корреляции rxy=-0,26 (связь слабая, обратная). Найдем коэффициент детерминации rxy2=(-0,26)2=0,07. Вариация результатаYна 7% объясняется вариацией фактора Х. Средняя ошибка аппроксимации 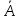 =11,17, что говорит о высокой ошибке аппроксимации (недопустимые пределы). В среднем расчетные значения отклоняются от фактических на 11,17%. =11,17, что говорит о высокой ошибке аппроксимации (недопустимые пределы). В среднем расчетные значения отклоняются от фактических на 11,17%. Проверяем F-критерий Фишера, для этого сравним Fтабл и Fфакт. Fтабл Общий вывод: Линейная парная модель плохо описывает изучаемую закономерность, т.к. не выполняются условия по коэффициенту детерминации и средней ошибке аппроксимации. Тема 4. Множественная регрессионная модель Множественная (многофакторная) регрессия – это регрессия между результирующей переменной Y и несколькими объясняющими переменными Х1, Х2, …, Хn. В общем виде уравнение множественной регрессии выглядит следующим образом: Y= 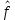 ( (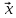 ), ), 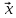 =x1,…xn. =x1,…xn.Для построения многофакторной регрессионной модели необходимо знать минимальный объем выборки, который зависит от числа факторов, включаемых в модель с учетом свободного члена. Для получения статистически значимой модели на один фактор требуется объем наблюдений, равный 5-8 наблюдениям. Определить минимальный объем выборки для получения статистически значимой модели можно по формуле: Nmin=5  (m+n), (m+n),где m – число факторов, включаемых в модель, n – число свободных членов в уравнении. На практике наиболее широко используется линейная множественная регрессия 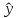 = а + b1х1 + b2х2 + b3х3 + b4х4 +…+ bnxn. Параметры при «х» называются коэффициентами «чистой» регрессии. Параметры b1, b2,…, bnпоказывают, на какую величину в среднем изменится результативный признак у, если переменную х увеличить на единицу измерения при фиксированном (постоянном) значении других факторов, входящих в уравнение регрессии. = а + b1х1 + b2х2 + b3х3 + b4х4 +…+ bnxn. Параметры при «х» называются коэффициентами «чистой» регрессии. Параметры b1, b2,…, bnпоказывают, на какую величину в среднем изменится результативный признак у, если переменную х увеличить на единицу измерения при фиксированном (постоянном) значении других факторов, входящих в уравнение регрессии.В большинстве случаев рассматриваются регрессионные модели, в которых в качестве объясняющих переменных выступают количественные переменные (производительность труда, доход и т.д.). Однако на практике достаточно часто возникает необходимость исследовать влияние качественных признаков, имеющих два или несколько уровней (градаций). К числу таких признаков можно отнести пол (мужской, женский), образование (начальное, общее, среднее и т.д.), фактор сезонности (зима, весна, лето, осень) и т.п. В связи с этим в модель вводят так называемые фиктивные переменные. Фиктивные переменные – это искусственно созданные переменные, для перевода качественных переменных в количественные. Обычно фиктивным переменным присваивают значения 0 и 1, но это не обязательно. Например:    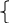 0, если кирпичный, 1, если панельный. Тип строения =  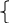 1, если кирпичный, 2, если панельный. Тип строения = Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение результирующей переменной при переходе от одной категории к другой при неизменных значениях остальных параметров. Если в модель включаются два или более тесно взаимосвязанных фактора, то наряду с уравнением регрессии появляется и другая линейная зависимость. Подобное явление, называетсямультиколлинеарностью. Мультиколлинеарность – попарная корреляционная зависимость между факторами. Мультиколлинеарная зависимость присутствует, если коэффициент парной корреляции 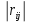  0,7. 0,7.Для устранения мультиколлинеарности используют метод исключения переменных. Он заключается в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Если т 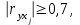 о одну из переменных можно исключить, но какую именно, решают исходя из управляемости факторов. Если возникает такая ситуация, когда оба фактора одновременно управляемы или нет, то решить вопрос об исключении того или иного фактора можно с помощью процедуры отбора главных факторов. Процедура отбора главных факторов включает обязательно следующие этапы: Производится анализ значения коэффициентов парной корреляции rij между факторами xi и xj. Анализ тесноты взаимосвязи объясняющих факторов с результативной переменной. Образец решения задачи контрольной работы: В табл. 4.1 приведены данные, формирующие цену на строящиеся квартиры в двух различных районах. Таблица 4.1
По имеющимся данным, представленным в таблице 4.1., получена матрица парных коэффициентов корреляции (табл. 4.2). Таблица 4.2
|
