Эконометрика. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе

• Название: Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе
• Анкор: Эконометрика
• Дата: 18.12.2022
• Размер: 202.39 Kb.
• Имя файла: Эконометрика.docx
• Тип: Краткое содержание; #851464
• страница: 5 из 7

Образец решения задачи контрольной работы:
Известно значение торгового предприятия за 12 месяцев (табл. 5.2).
Таблица 5.2

Месяц	Периоды, t	Доход, млн. руб.
Январь	0	111,01
Февраль	0,5236	120,2
Март	1,0471	125,21
Апрель	1,5707	113,45
Май	2,0943	98,35
Июнь	2,618	81,12
Июль	3,1416	65,87
Август	3,6652	57,87
Сентябрь	4,1888	55
Октябрь	4,7124	67,8
Ноябрь	5,236	79,01
Декабрь	5,7596	98,2

Для построения модели сезонных колебаний дохода торгового предприятия:

Необходимо вычислить коэффициенты по формулам: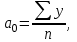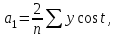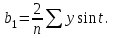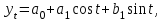








Расчеты удобно проводить в табл. 5.3:


Таблица 5.3

Месяцы	t	y	cost	sint	y*cost	y*sint
Январь	0,00	111,01	1,0000	0,0000	111,01	0,00
Февраль	0,52	120,20	0,8678	0,4969	104,31	59,72
Март	1,05	125,21	0,5002	0,8659	62,63	108,42
Апрель	1,57	113,45	0,0008	1,0000	0,09	113,45
Май	2,09	98,35	-0,4997	0,8662	-49,14	85,19
Июнь	2,62	81,12	-0,8670	0,4983	-70,33	40,42
Июль	3,14	65,87	-1,0000	0,0016	-65,87	0,10
Август	3,67	57,87	-0,8636	-0,5042	-49,98	-29,18
Сентябрь	4,19	55,00	-0,4990	-0,8666	-27,44	-47,66
Октябрь	4,71	67,80	-0,0004	-1,0000	-0,03	-67,80
Ноябрь	5,24	79,01	0,5035	-0,8640	39,78	-68,27
Декабрь	5,76	98,20	0,8662	-0,4996	85,06	-49,06
Сумма	-	1073,09	-	-	140,09	145,34

Получаем значения коэффициентов: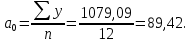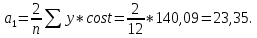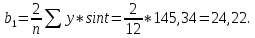




М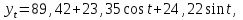
одель сезонных колебаний дохода торгового предприятия:
Далее необходимо рассчитать модель сезонных колебаний, последовательно подставляя в нее значения cost и sint (табл. 5.4).

Таблица 5.4

Месяцы	t	y	cost	sint	y*cost	y*sint	yt
Январь	0,00	111,01	1,0000	0,0000	111,01	0,00	112,77
Февраль	0,52	120,20	0,8678	0,4969	104,31	59,72	121,72
Март	1,05	125,21	0,5002	0,8659	62,63	108,42	122,08
Апрель	1,57	113,45	0,0008	1,0000	0,09	113,45	113,67
Май	2,09	98,35	-0,4997	0,8662	-49,14	85,19	98,74
Июнь	2,62	81,12	-0,8670	0,4983	-70,33	40,42	81,25
Июль	3,14	65,87	-1,0000	0,0016	-65,87	0,10	66,11
Август	3,67	57,87	-0,8636	-0,5042	-49,98	-29,18	57,05
Сентябрь	4,19	55,00	-0,4990	-0,8666	-27,44	-47,66	56,78
Октябрь	4,71	67,80	-0,0004	-1,0000	-0,03	-67,80	65,19
Ноябрь	5,24	79,01	0,5035	-0,8640	39,78	-68,27	80,25
Декабрь	5,76	98,20	0,8662	-0,4996	85,06	-49,06	97,55
Сумма	-	1073,09	-	-	140,09	145,34	1073,16

По фактическим и теоретическим значениям строим график ряда Фурье (рис. 5.1).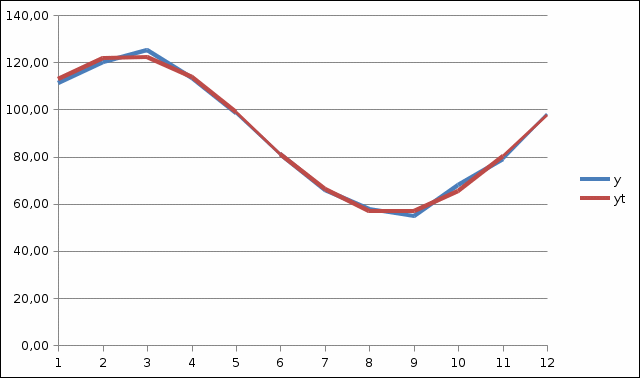

Рис. 5.1. График ряда Фурье по фактическим данным

Тема 6. Модели с распределенным лагом
Термин «динамический» характеризует каждый момент времени t в отдельности, а не весь период, для которого строится модель.

Модель является динамической, если в данный момент времени t она учитывает значение входящих в нее переменных, относящихся как к текущему, так и кпредыдущим моментам времени, то есть если эта модель отражает динамику исследуемых переменных в каждый момент времени. Например, на размер выручки от реализации или прибыль предприятия в текущем периоде могут оказывать влияние расходы на рекламу или проведение маркетинговых исследований, сделанные предприятием в предшествующие моменты времени.

ЛАГ – величина 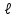, характеризующая запаздывание в воздействии фактора на результат.

Временной лаг - это показатель, отражающий отставание или опережение во времени одного явления по сравнению с другим (например, время от момента вложения средств до получения отдачи).

Модели с распределенным лагом– модели, содержащие не только текущие, но и лаговые значения факторных (объясняющих, экзогенных) переменных.
Предположим, что максимальная величина лага конечна, тогда модель примет вид: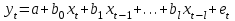


Модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной х, то это изменение будет влиять на значение переменной ув течение l следующих моментов времени.

Коэффициент регрессии b₀ при переменной х_t характеризует среднее абсолютное изменение у_t при изменении x_t на 1 единицу своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.

В момент (t + 1) совокупное воздействие факторной переменной x_t на результат у_t составит (b₀ + b₁) усл.ед.; в момент (t + 2) это воздействие можно охарактеризовать суммой (b₀ + b₁ + b₂) и т.д. Полученные таким образом суммы называют промежуточными мультипликаторами.

С учетом конечной величины лага (для максимального лага) можно сказать, что изменение переменой x_t в момент времени t на 1 условную единицу приведет к общему изменению результата через l моментов времени на (b₀ + b₁ +…+ b_l) абсолютных единиц.

Если ввести обозначение:b₀ + b₁ +…+ b_l = b, то величина b – долгосрочный мультипликатор. Он показывает абсолютное изменение в долгосрочном периоде (t + l) результата упод влиянием изменения на 1 единицу фактора х.