Эконометрика. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе
 Скачать 202.39 Kb. Скачать 202.39 Kb.
|
|
Вклад отдельного лага или относительные коэффициенты модели с распределенным лагом определяется по формуле: 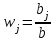 , ,где bj – коэффициенты при переменных; b – долгосрочный мультипликатор. При этом всегда выполняется свойство: 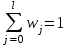 . .Кроме того, wj являются весами соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения результативного признака в момент времени (t + j). Зная величины wj, с помощью стандартных формул можно определить еще одну важную характеристику модели с распределенным лагом – величину среднего лага. Средний лаг модели представляет собой средний период, в течение которого будет происходить изменение результата под воздействием фактора в момент времени t: 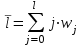 То есть он позволяет измерить скорость реакции у на изменение х. Малые значения среднего лага соответствуют относительно быстрой реакции результата уна изменение фактора х. Высокие значения говорят о том, что воздействие фактора х на результат у замедленно, т.е. будет сказываться в течение длительного периода времени. Образец решения задачи контрольной работы: Для модели Yt = 15 + 2xt+ 4xt-1 + 5xt-2 определите краткосрочный, промежуточный и долгосрочный мультипликаторы, вклад каждого лага, средний лаг модели. Решение. Краткосрочный мультипликатор – это коэффициент при xt, он равен 2.Следовательно, увеличение факторного показателя на одну единицу своего измерения приведет к среднему росту результативного показателя на 2 единицы своего измерения в том же периоде. В модели один промежуточный мультипликатор, его можно найти как 2 + 4 = 6. Следовательно, увеличение факторного показателя на одну единицу своего измерения приведет к среднему росту результативного показателя на 6 единиц своего измерения в момент времени t+1. Долгосрочный мультипликатор равен 2 + 4 + 5 = 11.В долгосрочной перспективе увеличение факторного показателя на одну единицу своего измерения приведет к среднему росту результативного показателя на 11 единиц своего измерения. Вклад каждого лага в модель равен: W1 = 2/11 = 0,18; W2 = 4/11 = 0,36; W3 = 5/11 = 0,45. Следовательно, 18% общего увеличения результативного показателя происходит в текущем моменте времени; 36% - в момент времени (t+1); 45% - в момент времени (t+2). Проверим свойство 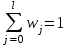 W1 + W2 + W3 = 0,18 + 0,36 + 0,45 ≈ 1. Средний лаг модели равен: 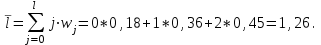 Большая величина лага (более 1 мес.) подтверждает, что большая часть эффекта роста результативного признака проявляется в течение длительного периода времени. ЗАДАНИЯ ДЛЯ ЗАНЯТИЙ СЕМИНАРСКОГО ТИПА И КОНТРОЛЬНОЙ РАБОТЫ Задание 1. Теоретические основы эконометрики 1.1.Определите, какие из перечисленных показателей относятся к временным данным, а какие к пространственным: урожайность ячменя в хозяйствах области; изменение курса акций; динамика потребительских цен; валовой сбор зерновых в 2003 году в хозяйствах области; объем производства предприятий области; товарооборот магазинов торговой сети; изменение курса евро за неделю; товарооборот магазина за 5 лет; показатель рождаемости регионов России; изменение рождаемости за первое полугодие в Новосибирской области. 1.2.Определите, какие из перечисленных показателей относятся к качественным, а какие к количественным: урожайность; численность работников; площадь помещения; тип строения здания; товарооборот; марка автомобиля; прибыль; образование; ассортимент выпускаемой продукции; форма собственности предприятия. 1.3.Определитев приведенных ниже парах показателей результирующую и объясняющую переменные: товарооборот и прибыль магазина; торговая площадь и товарооборот магазина; стаж работника и среднемесячная заработная плата; стоимость основных фондов и объем произведенной продукции; валовой сбор овощей и количество внесенных минеральных удобрений; стоимость квартиры и количество комнат. Определите форму и направление связи между результативным и факторным признаком, используя графический метод и метод сопоставления параллельных рядов. Номер таблицы для выполнения задания определяется в следующей таблице:
Таблица 1
Таблица 2
Продолжение таблицы 2
Таблица 3
Таблица 4
Таблица 5
Таблица 6
Таблица 7
Таблица 8
Таблица 9
Таблица 10
1.5. Определите направление и тесноту связи между результирующей переменной Y и объясняющей переменной Х с помощью линейного коэффициента корреляции, если известны следующие данные: 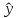 = 5,23 + (6,5 + (100/α))x и σx= 650 – α, σy= (550-α) = 5,23 + (6,5 + (100/α))x и σx= 650 – α, σy= (550-α)  10. 10. 1.6. Определите виды регрессий: 1. 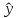 = 47,5 – 1,04х1+ 5х2 – 2,9х3 + е, = 47,5 – 1,04х1+ 5х2 – 2,9х3 + е,2. 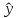 = 1/(11 + 10,45х1– 38,44х2 + 3,33 х3 – 1,37х4 + е), = 1/(11 + 10,45х1– 38,44х2 + 3,33 х3 – 1,37х4 + е),3. 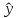 = e45,54 + 100x + е, = e45,54 + 100x + е,4. 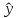 = -2x13x24x3e, = -2x13x24x3e,5. 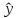 = 12,05-3х + е. = 12,05-3х + е.Покажите, где здесь результирующая и объясняющие переменные. Что обозначает «е» в уравнениях регрессии? Задание3. Информационные технологии эконометрических исследований Опишите историю и цель создания, а также основные функции и характеристики специализированных эконометрических пакетов.
Задание 4. Парная регрессионная модель 4.1. Назовите этапы эконометрического исследования. 4.2. По Российской Федерации за 2011 год известны значения двух признаков, представленных в таблице:
Для оценки зависимости Y от Хпостроена парная линейная регрессионная модель с помощью метода наименьших квадратов 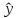 = а+bх+е, где а= = а+bх+е, где а=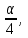 b= b=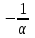 . Парный коэффициент корреляции rxy= . Парный коэффициент корреляции rxy=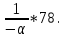 Средняя ошибка аппроксимации А= Средняя ошибка аппроксимации А=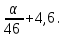 Известно, что Fтабл=4,96, а Fфакт= Известно, что Fтабл=4,96, а Fфакт=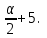 Определите коэффициент детерминации. Оцените линейную модель через среднюю ошибку аппроксимации и F-критерий Фишера. Определите коэффициент детерминации. Оцените линейную модель через среднюю ошибку аппроксимации и F-критерий Фишера.Задание 5.Множественная регрессионная модель По имеющимся данным, представленным в таблице 11, получена матрица парных коэффициентов корреляции (таблица 12). Таблица 11
Таблица 12
Задание: Запишите уравнение многофакторной регрессии и определите для нее минимальный объем выборки. Дайте экономическую интерпретацию полученной модели. Если известно, что а= 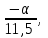 b1= b1=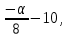 b2= b2=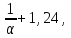 b3= b3=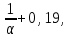 b4= b4=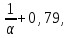 b5= b5=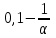 , b6= , b6=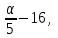 b7= b7=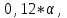 b8= b8=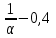 . . Укажите, какие фиктивные переменные использованы в модели. Проверьте факторы на мультиколлинеарность и устраните её. Запишите новое уравнение многофакторной регрессии, после устранения мультиколлинеарности. Задание 6. Модели временных рядов 6.1. Приведите примеры факторов, формирующих трендовую, сезонную и случайную компоненту. 6.2. Постройте модель сезонных колебаний дохода торгового предприятия, используя первую гармонику ряда Фурьепо данным, приведенным в таблице 13. Изобразите графически. |
