Эконометрика. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе
 Скачать 202.39 Kb. Скачать 202.39 Kb.
|
|
Задание: Запишите уравнение многофакторной регрессии и определите для нее минимальный объем выборки.Дайте экономическую интерпретацию полученной модели. Если известно, что а= 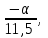 b1= b1=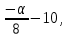 b2= b2=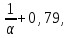 b3= b3=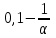 , b4= , b4=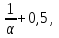 b5= b5=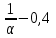 . .Укажите, какие фиктивные переменные использованы в модели. Проверьте факторы на мультиколлинеарность и устраните её. Запишите новое уравнение многофакторной регрессии, после устранения мультиколлинеарности. Решение. Пусть 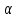 = 302. = 302.уравнение многофакторной регрессии будет выглядеть следующим образом: 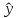 = -26,26 – 27,75х1 + 0,79х2 + 0,1х3 + 0,5х4 – 0,4х5. = -26,26 – 27,75х1 + 0,79х2 + 0,1х3 + 0,5х4 – 0,4х5.Экономическая интерпретация полученной модели: Квартиры в районе А стоят на 27,75% дешевле, чем в районе В. При увеличении общей площади на 1м2 стоимость квартиры возрастает на 0,79 тыс. $. При увеличении жилой площади на 1м2 стоимость квартиры увеличивается на 0,1тыс. $. При увеличении площади кухни на 1м2 стоимость квартиры увеличивается на 0,5тыс. $. При увеличении срока сдачи дома на 1 мес. стоимость квартиры уменьшается на 0,4тыс. $. Минимальный объем выборки определяем по формуле: Nmin=5*(m+n). В нашем случаем m = 5 (т.к. в модель включены 5 факторов), n = 1 (т.к. в модели 1 свободный член – «а»). Следовательно, Nmin=5*(5+1) = 30, т.е. для получения статистически значимой модели необходимо отобрать 30 квартир и собрать по ним необходимые данные. В модели использована 1 фиктивная переменная – наименование района, т.к. в построении модели участвуют 2 района – «а» и «б», которым присвоены количественные значения «1» и «2» соответственно. П 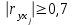 роверим факторы на мультиколлинеарность. Мультиколлинеарная зависимость присутствует, если Это условие выполняется для следующих пар факторов х3 и х2, х4 и х2, х4 и х3: 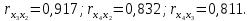 Найдены мультиколлинеарные факторы. Для устранения мультиколлинеарности используется метод исключения переменных. Будем исключать факторы, имеющие наименьшее значение 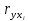 . .Рассмотрим первую пару мультиколлинеарных факторов 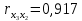 . Для исключения переменных необходимо знать, как каждый из факторных признаков связан с результативным признаком «Y». Эта зависимость отражается в последней строке матрицы парной корреляции. Итак, . Для исключения переменных необходимо знать, как каждый из факторных признаков связан с результативным признаком «Y». Эта зависимость отражается в последней строке матрицы парной корреляции. Итак, 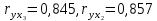 . Далее необходимо сравнить эти значения: . Далее необходимо сравнить эти значения: 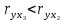 . Следовательно, факторный признак «х3» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х2». Аналогично, рассматриваются оставшиеся пары. . Следовательно, факторный признак «х3» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х2». Аналогично, рассматриваются оставшиеся пары.Вторая пара 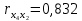 ; ; 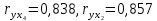 . . 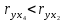 . Следовательно, факторный признак «х4» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х2». . Следовательно, факторный признак «х4» из модели можно исключить, т.к. его связь с результативным признаком меньше, чем у «х2».Третью пару 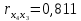 можно не рассматривать, т.к. и «х3» и «х4» из модели уже исключены. можно не рассматривать, т.к. и «х3» и «х4» из модели уже исключены.После устранения мультиколлинеарности уравнение многофакторной регрессии будет выглядеть следующим образом:  = а+b1х1+b2х2 +b5х5. = а+b1х1+b2х2 +b5х5.Минимальный объем выборки определим по формуле: Nmin=5*(m+n). В нашем случаем m = 3 (т.к. в модель включены 3 факторов), n = 1 (т.к. в модели 1 свободный член – «а»). Следовательно, Nmin=5*(3+1) = 20, т.е. для получения статистически значимой модели необходимо отобрать20 квартир и собрать по ним необходимые данные. Тема 5. Модели временных рядов Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов. Любой временной ряд включает два обязательных элемента: 1) показатель времени t, 2) значение показателя, или уровень ряда yi. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые можно разделить на три группы Факторы, формирующие тенденцию ряда (трендовая компонента T), Факторы, формирующие циклические или сезонные колебания ряда (циклическая или сезонная компонента S), Случайные факторы (случайная компонента Е). Временной ряд может иметь различное сочетание этих компонент. В экономике часто приходится иметь дело с сезонными колебаниями, т.е. когда показатель то повышается, то снижается на протяжении изучаемого периода с одинаковой частотой. Циклические (сезонные) колебания необходимо изучать и измерять для проведения определенных мероприятий, необходимых для их увеличения или уменьшения. Циклическая компонента S может быть разложена в ряд Фурье: 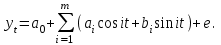 А 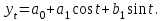 первая гармоника ряда Фурье будет выглядеть следующим образом: Г 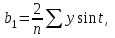 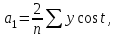 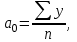 де параметры уравнения могут быть найдены по формулам: Если мы рассматриваем год как цикл, то n=12. Месячные периоды можно представить как части окружности, ряд внутригодовой динамики будет иметь следующий вид: Таблица5.1
|
