Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
Типовые задачи модуля III.Задача 3.1. Парная линейная регрессия и статистическая оценка ее достоверности с использованием инструмента «Регрессия» MS EXCELУсловие: имеются данные выборочного наблюдения за рынком строящегося жилья в Санкт-Петербурге (приложение 1).Требуется: изучить взаимосвязь между ценой квадратного метра общей площади квартир и расстоянием до ближайшей станции метро. Используя встроенный инструмент «Регрессия» MS EXCEL 2010, построить парную линейную модель регрессии, оценить достоверность полученных результатов. Решение. Прежде чем моделировать взаимосвязь переменных в виде уравнения регрессии, необходимо убедиться, что они действительно взаимосвязаны. Одним из приемов обнаружения корреляционной связи между двумя переменными является графический способ – построение точечного графика, где координатами точек являются соответствующие значения х и у в конкретных наблюдениях.. В нашем примере х- этофакторная переменная «расстояние до метро», у – результативная переменная «цена квадратного метра общей площади квартиры» (табл. 3.1.) . Табл. 3.1. Исходные данные
Исходные данные следует расположить в двух столбцах таблицы EXCEL, причем первый столбец – х, второй – у. Далее для построения графика нужно выделить столбцы с исходной информацией, войти в пункт меню «Вставка» и выбрать «Точечный график». Необходимо также дать название графика, подписать оси координат и указать место вывода графика на экран (рис.3.2.). Конфигурация точечного графика демонстрирует наличие обратной связи между переменными - с ростом переменной «х» среднее значение «у» имеет тенденцию к снижению. Следовательно, взаимосвязь между переменными есть, и она проявляется в том, что рост удаленности от метро в данной выборке наблюдений снижает цену квадратного метра жилья. 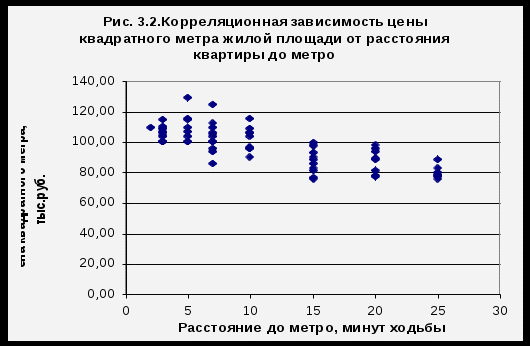 Для построения модели парной линейной регрессии выберите инструмент анализа «Регрессия». Чтобы активировать данную опцию, нужно войти в пункт меню «Файл», затем выбрать «Параметры». В нижней части окна «Параметры» Excel 2010 в раскрывшемся списке «Управление» следует выбрать «Надстройки Excel» и нажать клавишу «Перейти…». После чего, в открывшемся окне «Надстройки» поставить галочку у надписи «Пакет анализа». После выполнения процедуры активации для работы с надстройкой необходимо войти в пункт меню «Данные» и кликнуть по надписи «Анализ данных» в правой части ленты меню. В открывшемся окне «Анализ данных» нужно выбрать инструмент «Регрессия». Щелкните флажок напротив «Входной интервал У» и выделите соответствующий числовой диапазон (столбец) данных, аналогично заполните «Входной интервал Х». Далее укажите параметры вывода данных на экран: например, выберите «выходной интервал», щелкните флажок в окне напротив и укажите ячейку таблицы Excel , нажмите «ОК». В итоге появится лист со следующей информацией (табл.3.2.)
Раскроем содержание вывода итогов и условных обозначений. Таблица «Регрессионная статистика»: Множественный R – коэффициент корреляции, в нашем примере – парный коэффициент корреляции; R-квадрат – коэффициент детерминации; Нормированный R2 - это тот же коэффициент детерминации, но скорректированный на величину выборки. Нормированный R2=1-(1-R2)*((n-1)/(n-k)), где n - число наблюдений; k - число параметров в уравнении регрессии. Нормированный R2 предпочтительнее использовать в случае добавления новых регрессоров (факторов), т.к. при их увеличении будет также увеличиваться значение R2, однако это не будет свидетельствовать об улучшении модели; Стандартная ошибка показывает, на какую величину в среднем по всем наблюдениям фактические значения результативного признака будут отклоняться от их значений, определенных по уравнению регрессии. Наблюдения - указывается число наблюдений. Таблица «Дисперсионный анализ»: В первой графе таблицы представлены источники вариации зависимой переменной – регрессионная вариация (обусловленная влиянием изучаемого фактора), остаточная (влияние прочих факторов) и общая вариация (влияние всех причин); В столбце d.f. (degree of freedom) приводится число степеней свободы для каждого из источников вариации: d.f.общ. = n-1; d.f.регр.=m-1, где m –число параметров в уравнении регрессии; d.f.ост.= (n-1)-( m-1); В столбце SS (sum of squares) представлены суммы квадратов отклонений или объемы вариации зависимой переменной по источникам ее возникновения; MS (mid square) – средний квадрат отклонений или дисперсия зависимой переменной по источникам вариации; F - это фактическое значение критерия Фишера, определенное как отношение регрессионной дисперсии к остаточной (если первая больше второй); Значимость критерия Фишера : уровень значимости - это допустимая вероятность отвергнуть в результате проверки верную нулевую гипотезу. В рассматриваемом случае это означает вероятность признания по выборке наличие связи между переменными в генеральной совокупности, когда на самом деле ее там нет. Обычно уровень значимости принимается равным 0,05; В столбце «Коэффициенты» представлены параметры уравнения регрессии у=а+вх : «у-пересечение» - это свободный член уравнения регрессии а, коэффициент при переменной х есть коэффициент регрессии в; Стандартные ошибки параметров показывают, на какую величину в среднем по всем выборкам равного объема выборочные параметры связи (оценки) будут отличаться от истинных, генеральных параметров регрессии; t-статистика – это фактическое (выборочное) значение критерия t, которое равно отношению выборочного параметра к его стандартной ошибке; P-значение – это уровень значимости отдельных параметров уравнения регрессии; это вероятность того, что критическое значение используемого критерия (t-Стьюдента или t-нормального распределения) превысит значение, вычисленное по выборке. В данном случае сравниваем p-значения с выбранным уровнем значимости (0.05); Нижнее 95% и Верхнее % - это границы доверительного интервала данного параметра, определенные для 95% уровня вероятности суждения. Таблица «Вывод остатка» Предсказанное У – это рассчитанное по решенному уравнению регрессии значение зависимой переменной при данном значении фактора в каждом конкретном наблюдении; Остаток- это отклонение отдельной точки (наблюдения) от линии регрессии (предсказанного значения). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
