Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
 Скачать 2.09 Mb.
|
|
3. Условные обозначения примем аналогичными для задачи 1.6, где уже был выполнен расчет объемов вариации по источникам варьирования: Wобщ.= 10302, Wфактора.(межгр.)=2078, Wостаточная (внутригрупп.)=8224. 4. Рассчитаем число степеней свободы для каждого источника варьирования. В задаче общее число наблюдений (квартир) N=68, число групп (районов)=4. Для общего объема вариации число степеней свободы равно d.f.общ.= N-1=67 Число степеней свободы для факторной дисперсии: d.f.фактор.=m-1=4-1=3 Число степеней свободы для остаточной дисперсии: d.f.ост.=( N-1)-( m-1)=67-3=64 5. Рассчитаем дисперсии цены за 1 м2 в зависимости от источника вариации: Дисперсия по фактору  ;Дисперсия остаточная  6. Определим фактическое значение критерия Фишера по формуле 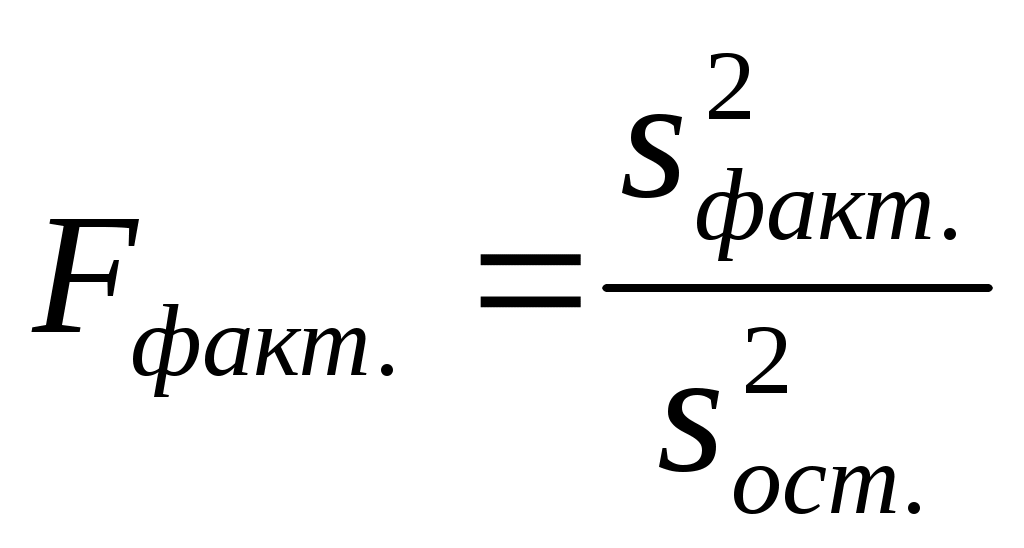 (где s2факт.> s2ост.):  7. В приложении 4 найдем теоретическое (табличное) значение критерия F-распределения при заданном уровне значимости 0,05 и соответствующих значениях числа степеней свободы (столбец – 3, строка – 64): Fтабл.= 2,75 8. Результаты решения запишем в таблицу 2.6. Табл.2.6 Расчет и анализ дисперсий
Сделаем вывод. Так как фактическое значение критерия F превышает табличное, оно попадает в критическую область. В этом случае нулевая гипотеза о равенстве средних величин признака в генеральных совокупностях должна быть отвергнута. Принимаем альтернативную гипотезу. С вероятностью 0,95 можно утверждать, что между средними ценами 1 м2 жилья в разных районах имеются существенные различия. 2.3.2. Конкретизация дисперсионного анализа на основе метода контрастов Шеффе. Условие: по результатам дисперсионного анализа сделан общий вывод о существенном различии цен на 1м2 жилья в различных районах Санкт-Петербурга. Требуется: проверить статистические гипотезы относительно достоверности всех попарных различий между районами. Решение. 1. Сформулируем статистические гипотезы относительно двух средних величин в генеральных совокупностях, учитывая при этом все возможные варианты попарного сравнения:
2. Рассчитаем по выборочным данным контрасты, то есть разности выборочных средних, используя данные таблицы 2.5:             3. Для каждого выборочного контраста найдем его среднее квадратическое отклонение по формуле:       4. Рассчитаем фактические значения критерия Шеффе как отношение каждого из контрастов к его среднему квадратическому отклонению:   ;  ;  ;  ; ;  5. Теоретическое значение критерия равно  , где т – число групп, Fтабл.- табличное значение критерия Фишера, определенное с учетом заданного уровня значимости 0,05 и числом степеней свободы для факторной и остаточной дисперсии (d.f.факт.=3 и d.f.ост.=64). Fтабл.=2.75 (приложение 4). 6. Сравним фактические значения критерия Шеффе с теоретическим и сделаем вывод:  >2,87 , принимаем альтернативную гипотезу На:   <2,87, принимаем нулевую гипотезу Но:   <2,87, принимаем нулевую гипотезу Но:   <2,87, принимаем нулевую гипотезу Но:   >2,87, принимаем альтернативную гипотезу На:   <2,87. принимаем нулевую гипотезу Но:  .Иными словами, по данным выборочного наблюдения мы доказали, что жилье в новостройках Калининского района Санкт-Петербурга существенно дороже жилья в Приморском и Выборгском районах, а также существенно дороже, чем в Красносельском районе. Во всех остальных вариантах попарного сравнения районов с уровнем значимости 0,05 мы можем гарантировать, что различия в ценах носят несущественный, недостоверный характер, обусловленный случайным характером наблюдений. Вопросы для проверки знаний по модулю II. 1. В чем состоит сущность выборочного метода наблюдения? При каких условиях его применение целесообразно? 2. Каковы научные условия применения выборочного наблюдения? 3. Что такое ошибка выборки? 4. Какие виды ошибок выборочного наблюдения Вы знаете? 5. Что показывает конкретная ошибка выборки? 6. Какова интерпретация средней ошибки выборки? 7. Как рассчитать среднюю ошибку выборки? 9. Как рассчитывается предельная ошибка выборочной средней для больших и малых выборок? 10. Что такое точечная и интервальная оценка генеральной средней? 11. Как определяется ошибка выборочной доли? 12. Дайте определение статистической гипотезы. 13. Каково содержание нулевой (рабочей) и альтернативной гипотез? 14. В чем смысл уровня значимости при проверке статистической гипотезы? 15. Опишите схему проверки статистической гипотезы о равенстве средних по данным двух независимых выборок. 16. В каком случае принимается нулевая гипотеза? 17. Как формулируется нулевая гипотеза в дисперсионном анализе? 18. Какие критерии применяются в дисперсионном анализе для оценки различий: а) нескольких выборочных средних; б) отдельных пар средних величин при формировании выборок разной численности? 19) Как рассчитывается фактическое значение критерия Фишера? 20) Как найти табличное значение критерия Фишера? 21) В каком случае принимается нулевая гипотеза в дисперсионном анализе? 22) При каких обстоятельствах и почему проводится попарное сравнение средних величин по результатам дисперсионного анализа? Модуль III. Парный линейный корреляционно-регрессионный анализ. Целью изучение модуля III является приобретение практических навыков построения корректных парных линейных регрессионных моделей, пригодных для дальнейшего анализа и прогнозирования. Студенты должны уметь определять параметры уравнения, давать им смысловую интерпретацию, оценивать достоверность модели в целом и отдельных ее параметров, выполнять точечный и интервальный прогноз. Методические указания. Каждая единица статистической совокупности имеет множество качественных и количественных признаков (х,y,z и т.д.). Например, объекты недвижимости имеют такие признаки, как размер, стоимость, территориальная принадлежность, удаленность от центра, форма собственности и т.д. Между признаками существуют связи: так, например, чем больше площадь земельного участка, тем, при прочих равных условиях, выше его стоимость. Удаленность от центра города, наоборот, снижает стоимость земельного участка. Все возможные связи между признаками можно разделить на две группы: функциональные и статистические. Признаки находятся в функциональной зависимости, когда связь между ними задается математическим уравнением, справедливым для любого случая. Например, если у - стоимость квартиры, х – ее общая площадь, а z – цена квадратного метра, то взаимосвязь этих признаков имеет вид у=х · z. Таким образом, зная значения двух переменных, мы по этому уравнению можем точно определить значение третьей переменной. Полная зависимость одного признака от другого (или других) позволяет охарактеризовать функциональные связи как полные связи. Статистические зависимости, в отличие от функциональных, являются неполными, поскольку конкретному значению одного признака могут соответствовать несколько значений другого. Так, например, мы знаем, что стоимость квартиры зависит от расстояния до ближайшей станции метро. Однако при равной удаленности от метро цена различных квартир будет разной. Неполные статистические связи проявляются не в каждом конкретном случае, а только при большом числе наблюдений в виде изменения среднего значения одного признака, связанного с изменением другого. При положительной статистической связи (ее называют также прямой) по мере роста одного признака наблюдается рост другого. При отрицательной (обратной) связи по мере роста одного признака снижается значение другого. Важно различать корреляционные и регрессионные взаимосвязи. Корреляционные связи характеризуют сопряженное изменение признаков безотносительно причинно-следственных зависимостей, а регрессионные – связи между причиной и следствием. Таким образом, регрессионные связи являются направленными, характеризующие влияние факторных признаков на результативные. Регрессионные зависимости статистика описывает посредством математических уравнений, получивших название уравнений регрессии. Задачами корреляционно-регрессионного анализа являются: 1) определение абсолютного и относительного изменения зависимой (результативной) переменной при изменении независимой переменной (факторного признака); 2) определение тесноты связи между признаками и доли вариации результативного признака, обусловленной влиянием изучаемых факторных признаков; 3) статистическая оценка достоверности корреляционных и регрессионных связей между признаками в генеральной совокупности на основе выборочных данных; Первая задача реализуется путем составления и решения уравнения регрессии, описывающего регрессионную связь. Самым эффективным методом решения уравнения регрессии является метод наименьших квадратов (МНК). Основное условие МНК – минимизация отклонений фактических значений результативного признака уi от значений, определенных по уравнению регрессии 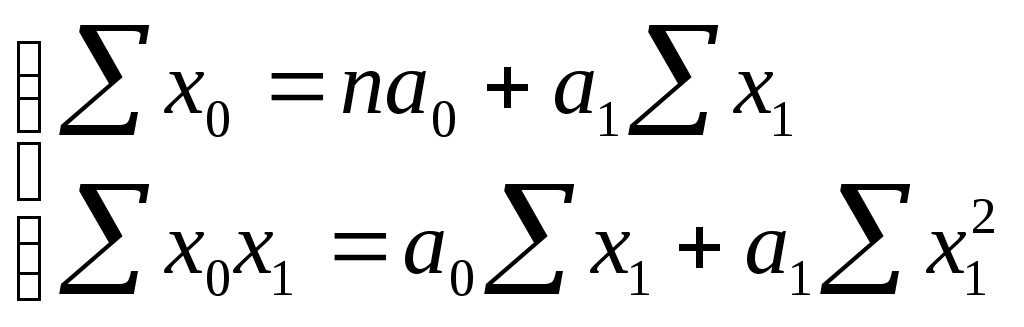 : ∑( уi- )2→min. Для отыскания параметров ао и а1 парного линейного уравнения регрессии у= ао+ а1х, при которых отклонения принимают минимальные значения, частные производные выбранной функции приравнивают к нулю и путем математических преобразований получают систему так называемых нормальных уравнений  . Поскольку суммы значений признаков, их произведений, а также их квадратов мы можем найти по первичной базе данных, то в итоге получаем два уравнения с двумя неизвестными. Решив систему уравнений, мы получаем значения параметров и уже сможем записать уравнение регрессии в решенном виде. Полученные параметры можно истолковать следующим образом. Коэффициент при х (коэффициент наклона) показывает, что если х увеличивается на одну единицу, то у возрастает на величину а1. Как х, так и у измеряются в своих единицах измерения.Постоянная ао уравнения показывает прогнозируемый уровень у, когда х = 0. Иногда это имеет ясный смысл, иногда нет. Если х = 0 находится достаточно далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам. Например, если мы изучаем зависимость стоимости квартиры от ее площади, то х = 0 означает бессмысленную ситуацию, когда у квартиры нет площади. В подобных случаях параметр ао в уравнении не подлежит смысловой интерпретации и называется условным началом. Относительную величину изменения зависимой переменной при изменении независимой переменной можно определить по коэффициенту эластичности (Э), который покажет, на сколько процентов изменится в среднем результативный признак при изменении факторного на один процент. Расчет проводится по формуле:  . Величина коэффициента эластичности указывает на силу реакции результативного признака на относительный прирост фактора: если Э≤1 – эластичность слабая; Э=1 – эластичность средняя; Э≥1 – эластичность высокая.Вторая задача корреляционно-регрессионного анализа решается с помощью статистических показателей тесноты связи, к которым относятся коэффициент детерминации и коэффициент корреляции. В основе расчета коэффициента детерминации лежит разложение общего объема вариации зависимой переменной на вариацию, воспроизведенную уравнением регрессии, и остаточную вариацию:  Коэффициент детерминации представляет собой отношение воспроизведенной уравнением вариации к общей вариации зависимой переменной:  . Из этой формулы следует, что чем ближе коэффициент детерминации к единице, тем сильнее факторный признак влияет на результативный, и тем теснее связь между ними. Коэффициент корреляции – это корень квадратный из коэффициента детерминации:  . Для коэффициента корреляции разработаны шкалы меры тесноты связи. В практических исследованиях часто ориентируются на следующий вариант шкалы:До 0,3 - связь практически отсутствует; 0,3 – 0,5 - связь слабая; 0,5 – 0,7 - связь умеренная (средняя); 0,7 – 0,9 - связь тесная (сильная); 0,9-0,99 – связь очень тесная (близка к функциональной). Третья задача корреляционно-регрессионного анализа – статистическая оценка достоверности корреляционных и регрессионных связей между признаками. Наиболее точные характеристики связи можно получить лишь в том случае, если исследователь опирается на всю совокупность фактов и событий определенного рода, то есть если удалось провести сплошное наблюдение генеральной совокупности. Если же уравнение регрессии определено по выборочным данным, то важно помнить о том, что вся интерпретация уравнения в действительности представляет собой лишь оценку реальных соотношений взаимосвязанных признаков в генеральной совокупности. Кроме того, уравнение регрессии отражает только общую закономерность для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. Поэтому, если выборочные характеристики взаимосвязи переменных необходимо распространить на генеральную совокупность, то следует провести статистическую оценку их достоверности или существенности. Под достоверностью в математической статистике понимают вероятность того, что значение проверяемого показателя связив генеральной совокупности не равно нулю и не включает в себя величины противоположных знаков. Недостоверный (несущественный) показатель формируется под влиянием случайных причин. Оценка на достоверность проводится на основе проверки статистических гипотез по параметрическим критериям по общей схеме проверки гипотез: 1) выдвигается нулевая гипотеза об отсутствии корреляционной связи в генеральной совокупности; 2) выбирается статистический критерий для проверки гипотезы; 3) рассчитывается фактическое значение критерия; 4) фактическое значение критерия сравнивается с теоретическим его значением при установленном уровне значимости; если фактическое значение критерия меньше табличного, то принимается нулевая гипотеза, если фактическое значение критерия больше табличного – принимается альтернативная гипотеза. На достоверность связи оцениваются: 1) уравнение регрессии в целом; 2) отдельные параметры уравнения; 3) коэффициент корреляции и коэффициент детерминации. Первая процедура проводится на основе дисперсионного анализа с помощью F-критерия Фишера, поэтому она получила название F-теста уравнения регрессии. Ее назначение - сделать вывод о правильности выбора вида взаимосвязи и дать характеристику достоверности всего уравнения регрессии в целом. Фактическое значение критерия Фишера определяется как отношение регрессионной и остаточной дисперсии: 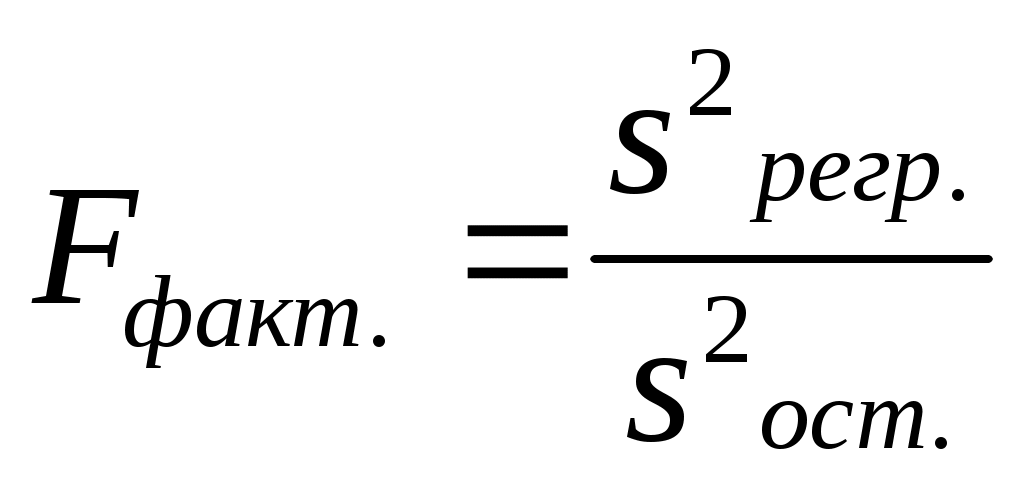 Для опровержения нулевой гипотезы необходимо, чтобы регрессионная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором были разработаны таблицы критических значений F-отношений (Fтабл.) при разном уровне существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения двух выборочных дисперсий (если выборки произведены из одной генеральной совокупности), которая может иметь место при случайном их расхождении для данного уровня вероятности суждения. Уравнение регрессии признается достоверным, если фактическое (вычисленное) значение F-критерия больше табличного. Вторая процедура - оценивание достоверности коэффициента регрессии – также проводится по общей схеме проверки гипотез. Сначала выдвигается нулевая гипотеза об отсутствии связи между признаками и равенстве коэффициента регрессии в генеральной совокупности нулю- Н0: β =0.Средняя (стандартная) ошибка коэффициента регрессии для парной линейной связи определяется по формуле: 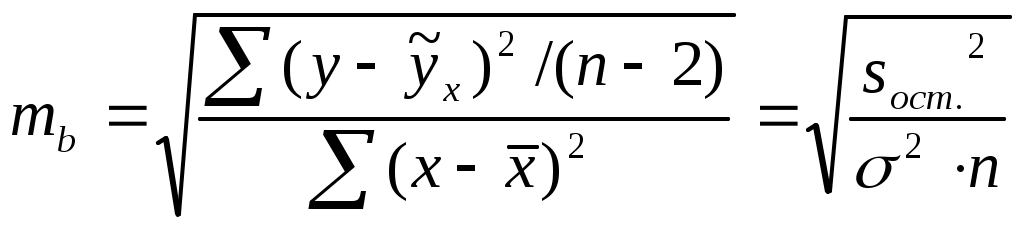 Для оценки достоверности коэффициента регрессии его выборочная оценка в сравнивается с величиной стандартной ошибки, то есть определяется фактическое значение t-критерия Стьюдента tфакт.=  , которое потом сравнивается с табличным значением tтабл. при определенном уровне значимости λ и остаточном числе степеней свободы dfост.. Нулевая гипотеза отклоняется при tфакт.> tтабл. Доверительный интервал для коэффициента регрессии определяется как в - tтабл.∙ т в ≤ β ≤ в + tтабл.∙ т в 3.11. Поскольку коэффициент регрессии в линейном уравнении связи имеет четкую смысловую интерпретацию, то доверительные границы коэффициента не должны содержать противоречивых значений, например -0,8 ≤ β ≤ 1,2. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит отрицательные и положительные величины и даже ноль, чего не может быть. Третья процедура - алгоритм оценки достоверности выборочных коэффициентов корреляции - предусматривает расчет критериев достоверности t-Стьюдента (для малых выборок) и t-нормального распределения (для больших выборок) как отношения выборочного коэффициента корреляции к его средней ошибке : tr =  Выборочный показатель связи rобеспечивает точечную оценку рассматриваемого параметра, но при этом вероятность того, что истинное значение будет в точности равно этой оценке, ничтожно мала. Доверительный интервал дает так называемую интервальную оценку параметра, то есть диапазон значений, который будет включать истинное значение с высокой, заранее определенной вероятностью. Для расчета доверительного интервала необходимо найти предельную ошибку коэффициента корреляции по формуле  = tst ∙mr. Предельная ошибка покажет, на какую максимальную величину для данного уровня вероятности выборочный коэффициент корреляции r может отличаться от генерального коэффициента корреляции p. Доверительный интервал для коэффициента корреляции определяется как  .Таким образом, применение регрессионного метода в условиях малочисленных или выборочных наблюдений предполагает обязательную последующую оценку достоверности полученных параметров связи. Предлагаемые в данном разделе методики дают возможность выявить случайную или закономерную природу зависимости между факторами и результатами. Только наличие устойчивой зависимости дает возможность проводить нормативные и прогнозные расчеты и, тем самым, получать верные выводы о развитии экономических явлений и процессов. Важным направлением использования уравнений связи является их применение для прогнозирования ожидаемых результатов при заданном уровне факторов. Использование регрессионной модели для прогнозирования состоит в подстановке в уравнение регрессии ожидаемых значений факторных признаков для расчета точечного прогноза результативного признака и его доверительного интервала с заданной вероятностью. Поскольку не все значения результативного признака лежат на линии регрессии, то использование уравнения регрессии для прогнозирования приведет к некоторой погрешности (ошибке) в оценке анализируемого показателя. Можно назвать два источника возникновения этой погрешности. Во-первых, решенное по выборочным данным уравнение регрессии является всего лишь одним из множества возможных по воле случая подобных уравнений. Каждое из них является лучшим или худшим приближением к истинной (генеральной) линии связи. Во-вторых, уравнение регрессии не воспроизводит общую вариацию результативного признака в полном объеме; остаточная вариация вносит свой вклад в величину погрешности (ошибки) прогноза. Ошибка точечного прогноза или ошибка положения линии регрессии  покажет, на какую величину в среднем точечные прогнозы  по всем возможным выборочным линиям регрессии будут отличаться от прогнозного значения результативного признака, определенного по истинной (генеральной) линии связи. Она определяется по формуле: 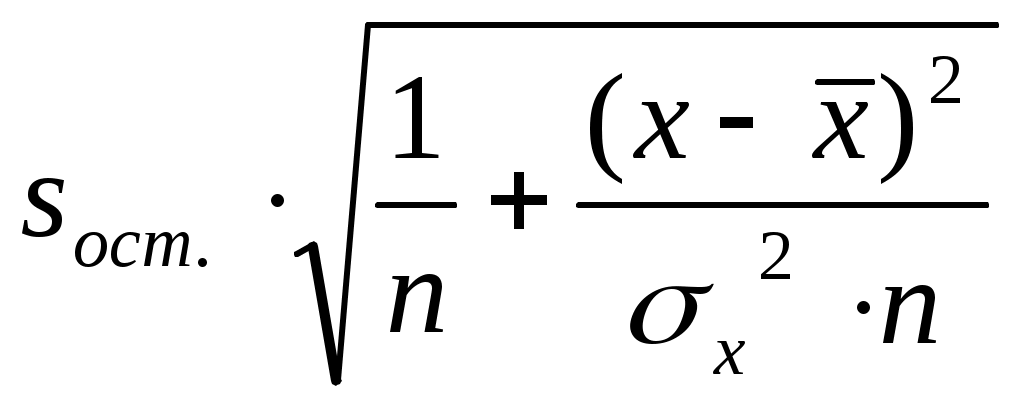= . Из данной формулы видно, что ошибка положения линии регрессии в прогнозной точке зависит от величины остаточной дисперсии и от того, как сильно значение признака-фактора отклоняется от его среднего значения. Чем больше разность  , тем больше ошибка , с которой предсказывается значение для заданного значения х. Доверительные интервалы положения линии регрессии при заданном х определяются выражением 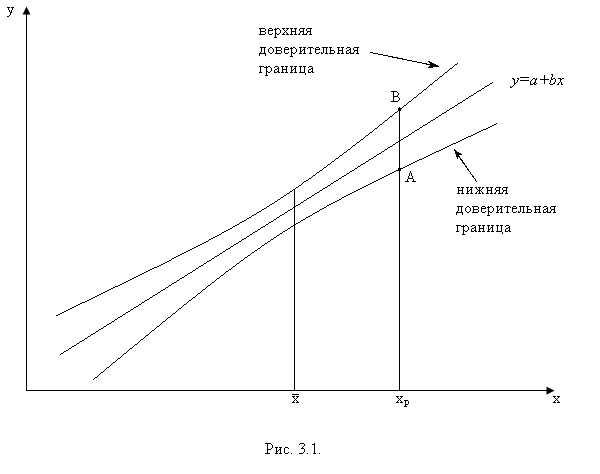 где – α уровень значимости. На рисунке 3.1. доверительные границы для представлены гиперболами, расположенными по обе стороны от выборочной линии регрессии.  Однако фактические значения yi отклоняются от уравнения регрессии на величину случайной ошибки  , которая оценивается как остаточная дисперсия на одну степень свободы s2ост/d.f.. Поэтому ошибка прогноза индивидуального значения yi должна учитывать не только ошибку положения линии регрессии, но и остаточную вариацию. Средняя ошибка прогнозируемого индивидуального значения результативного признака yi(х) составит Доверительный интервал индивидуального прогноза  дает возможность в каждом отдельном случае с определенной вероятностью указать, что величина результативного признака окажется в определенном интервале относительно значения, вычисленного по уравнению связи. | ||||||||||||||||||||||||||||||||||
