Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки

• Название: Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
• Дата: 14.10.2022
• Размер: 2.09 Mb.
• Имя файла: uch-met_posobie_statistika-metod_ukazania_po_resheniyu_tip_zadac.doc
• Тип: Методические указания; #734355
• страница: 6 из 20

Типовые задачи модуля II

Задача 2.1 Точечная и интервальная оценка параметров генеральной совокупности по данным выборки

2.1.1. Точечная и интервальная оценка среднего значения признака в генеральной совокупности по данным большой выборки

Условие: имеются данные выборочного наблюдения за ценами 1 м² общей площади по 37 квартирам Выборгского и Приморского районов Санкт-Петербурга (таблица 2.1.).

Требуется провести точечную и интервальную оценку среднего значения цены квадратного метра в этих районах.

Решение:

1. 
   Определим квадраты значений признака (х_i²) и запишем их в таблицу 2.1.
   

2. Подсчитаем и и также запишем в таблицу 2.1.

Таблица 2.1. Цена квадратного метра общей площади квартир Выборгского и Приморского районов Санкт-Петербурга по результатам выборочного наблюдения

№ наблюде-ния	Цена 1 м2, тыс.руб.	Квадрат значения признака	№ наблюде-ния	Цена 1 м2, тыс.руб.	Квадрат значения признака
	Х i	Х i2		Х i	Х i2
1	81,31	6611,59	20	100,00	10000,00
2	75,96	5770,26	21	100,12	10023,91
3	75,97	5771,92	22	100,13	10026,58
4	76,84	5904,49	23	100,14	10028,15
5	77,15	5951,83	24	100,15	10029,39
6	77,44	5996,32	25	100,21	10041,11
7	77,59	6019,62	26	104,08	10832,99
8	78,00	6084,00	27	104,65	10951,87
9	78,95	6232,69	28	105,66	11164,12
10	80,17	6427,82	29	106,77	11399,17
11	81,54	6648,52	30	107,00	11448,38
12	82,90	6872,17	31	108,64	11803,08
13	83,24	6929,44	32	109,05	11892,07
14	85,93	7383,26	33	109,22	11928,98
15	85,95	7386,71	34	109,90	12078,92
16	99,85	9970,82	35	110,00	12100,00
17	100,00	10000,00	36	110,00	12100,00
18	100,00	10000,00	37	110,26	12156,48
19	100,00	10000,00
Итого				3474,96	335966,64

3. 
   Вычислим среднюю величину по данным выборочной совокупности:
   

(тыс.руб.)

4. 
   Найдем выборочную дисперсию:
   

5. 
   Исчислим несмещенную оценку¹ дисперсии:
   

Несмещенная оценка дисперсии может быть исчислена также без определения выборочной дисперсии по формуле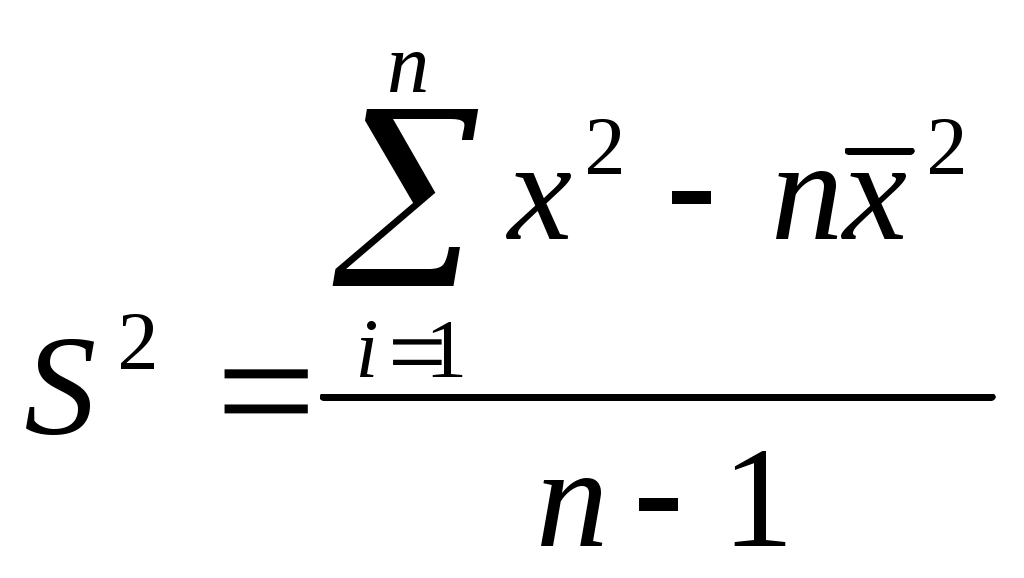

6. 
   Рассчитаем среднюю ошибку выборочной средней для случайного бесповторного отбора:
   

(тыс.руб.)

Примечание: так как число выборки по отношению к числу единиц генеральной совокупности чрезвычайно мало, то поправочным коэффициентом можно пренебречь.

7. 
   Проведем точечную оценку средней в генеральной совокупности:
   

(тыс.руб.) при m_x = 2,68 тыс.руб

7. 
   По таблице "Значение интеграла вероятностей при разных значениях t" (приложение 1) найдем теоретическое значение t при доверительном уровне вероятности : t_0,95=1,96.
   
8. 
   Определим предельную случайную ошибку выборочной средней:
   

9 (тыс.руб.)

10. 
    Проведем интервальную оценку, т.е. найдем интервал, в котором с заданным уровнем вероятности находится средняя генеральной совокупности:
    

или (тыс.руб.)

11. 
    Вывод: с доверительным уровнем вероятности 0,95 можно утверждать, что средняя цена 1м² квартир в Выборгском и Приморском районах Санкт-Петербурга в период наблюдения находилась в пределах от 88,66 до 99,18 тыс.руб.
    

2.1.2. Точечная и интервальная оценка средней величины генеральной совокупности по данным малой выборки.

Условие: имеются данные выборочного наблюдения о рынке строящегося жилья Калининского района Санкт-Петербурга.

Требуется: провести оценку средней цены одного квадратного метра общей площади квартир в новостройках Калининского района Санкт-Петербурга.

Таблица 2.2. Цена 1 м² общей площади квартир Калининского района

Санкт-Петербурга

№ квартиры	Цена 1м2, тыс.руб., хi	Квадрат значения признака, xi2	№ квартиры	Цена 1м2, тыс.руб. хi	Квадрат значения признака, xi2
1	103,92	10799,69	6	106,10	11256,69
2	103,98	10810,91	7	115,00	13225,00
3	104,05	10827,25	8	115,06	13237,92
4	105,98	11231,77	9	115,16	13262,12
5	106,08	11253,54	10	115,24	13279,82
Итого				1090,57	119184,73

Решение:

1 .Определим квадраты значений признака (x_i²) и запишем их в таблицу 2.2.

2. Подсчитаем суммы ∑ х_i и ∑ x_i² и запишем их в итоговую строку таблицы 2.2.

3. Вычислим среднюю величину цены квадратного метра по данным выборочной совокупности:

(тыс.руб.)

4.Найдем выборочную дисперсию:

^*

*Дисперсию варьирующего признака можно определить с помощью программы Excel: Вставка→Функция→Категория функций (статистические)→Выбираем « диспр». Далее в диалоговом окне указываем входной интервал данных и получаем результат.
5. Исчислим несмещенную оценку дисперсии:

6. 
   Исчислим среднюю ошибку выборочной средней:
   

(тыс.руб.)

Примечание: так как число выборки по отношению к числу единиц генеральной совокупности чрезвычайно мало, то поправочным коэффициентом можно пренебречь.

7. 
   Проведем точечную оценку средней в генеральной совокупности:
   

(тыс.руб.) при m_x = 1,67(тыс.руб.)

7. 
   По таблице "Значения двухстороннего критерия t-Стьюдента (приложение 3) найдем теоретическое значение t при доверительном уровне вероятности и числе степеней свободы вариации d.f. = п-1 = 9: t_0,95=2,26.
   
8. 
   Определим предельную случайную ошибку выборочной средней:
   

(тыс. руб.)

10. Проведем интервальную оценку средней в генеральной совокупности:

(тыс. руб.) или



Сделаем вывод. С доверительным уровнем вероятности 0,95 можно утверждать, что средняя цена за квадратный метр общей площади квартир в новостройках Калининского района Санкт-Петербурга находится в пределах от 105,29 до 112,83 тыс.руб.
2.1.3. Точечная и интервальная оценка доли альтернативного признака в генеральной совокупности по данным выборки.

Условие: имеются данные выборочного наблюдения о рынке вновь строящегося жилья в Санкт-Петербурге.

Требуется: по результатам выборочного наблюдения дать оценку доли относительно дешевого жилья (менее 100 тыс.руб. за 1 м²) в новостройках Санкт-Петербурга.

Решение:
1. Определим выборочную долю признака. В исходной базе данных (приложение 1) из 68 наблюдений 33 квартиры имеют цену квадратного метра менее 100 тыс. руб. Следовательно, выборочная доля относительно дешевого жилья в новостройках составляла р=33/68=0,48, а доля дорогого жилья , соответственно g=1-0,48=0,52.

2. Определим дисперсию альтернативного признака как произведение его долей (см. задачу 1.5): σ²=pg=0,48·0,52=0,25

3. Рассчитаем среднюю ошибку выборочной доли по формуле:



4. По таблице «Значения двухстороннего критерия t-Стьюдента

(приложение 3) найдем теоретическое значение t при доверительном уровне вероятности и числе степеней свободы вариации d.f. = п-1 = 9: t_0,95=2,26.

5. Проведем точечную оценку доли относительно дешевого жилья в генеральной совокупности (в новостройках Санкт-Петербурга):

при m_р= 0,087

6. Определим предельную случайную ошибку выборочной доли:



7. Проведем интервальную оценку доли в генеральной совокупности:

или р_{выб .}-ε<sub>р ;

0,48 - 0,196 ; 0,28</sub>