Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
3. Построим ранжированный ряд распределения квартир по цене1 м2 общей площади, то есть расположим квартиры в порядке возрастания цены, указав номер квартиры по ранжиру и по списку таблицы 1.1. и табл. 1.4.Табл. 1.4. Ранжированный ряд распределения квартир по цене за 1 кв.м
Изобразим ранжированный ряд графически посредством огивы Гальтона, для чего в прямоугольной системе координат построим точечный график: абсциссы точек - номера единиц в ранжированном ряду, ординаты - соответствующие им значения признака «цена за 1 м 2» (рис.1.2). 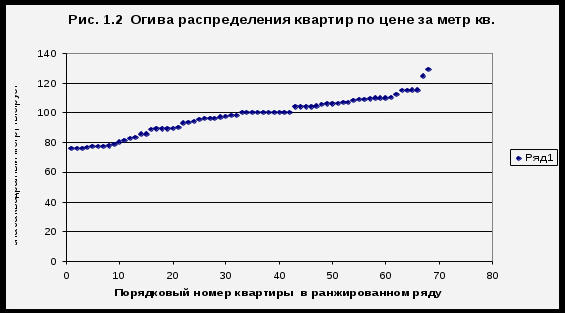 Вывод: Ранжированный ряд распределения и его график показывают, что в изучаемой совокупности значение признака от единицы к единице изменяется в основном плавно, постепенно. Минимальное значение признака – 75,87 тыс.руб., максимальное значение признака – 129,2 тыс.руб.. Интервальный ряд распределения как способ упорядочения статистических данных строится в том случае, если группировочный признак является непрерывным по своей природе (результат деления одной величины на другую), либо же он дискретный, но варьирует в широких границах. Построение интервального ряда проводится в следующей последовательности: а) определение группировочного признака, т. е. признака, по которому следует формировать группы; б) построение ранжированного ряда по группировочному признаку (смотри табл. 1.4 и рис. 1.2); в) анализ характера нарастания признака в ранжированном ряду по огиве Гальтона; г) определение числа групп; д) определение шага интервала (h); е) определение границ интервалов; ж) подсчет числа единиц (частот встречаемости) в каждом интервале; з) табличное и (или) графическое представление ряда распределения; и) выводы. В нашем примере группировочным признаком будет цена 1 м2 в тыс. руб. Этот признак является непрерывным, поскольку определяется делением стоимости квартиры на ее общую площадь. Результат деления может быть определен с любой степенью точности (до десятых долей, сотых и т.д.). В этом случае мы не можем в таблице указать все возможные отдельные варианты признака – таблица оказалась бы слишком громоздкой, не удобной для чтения и анализа. В этом случае целесообразно признак задать интервалом (от…до…), то есть требуется построить интервальный ряд распределения. Способ определения числа групп зависит от характера нарастания признака в ранжированном ряду, что позволяет увидеть огива Гальтона (рис.1.2). При неравномерном, скачкообразном нарастании признака следует формировать группы с неравными интервалами. Число групп определяется по количеству «скачков», т.е. резких переходов от одних значений признака к другим. При равномерном изменении признака формируются группы с равными интервалами, и их число определяется по формуле Стерджесса: m=1+3.322 lg N, где N – число единиц в совокупности. При численности совокупности менее 50 единиц, число групп можно определить как корень квадратный из числа наблюдений: m= В нашем примере изменение признака равномерное (на графике нет резких переходов от одного значения цены к другому), поэтому определяем число интервалов по формуле m=1+3.322 lg 68 =1+3.322*1,83= 7,07. Учитывая, что число групп не может быть дробным, остановимся на 7 группах (интервалах). При равномерном изменении признака шаг интервала рассчитывается по формуле: h= Как правило, шаг интервала задается с такой же степенью точности, что и группировочный признак: в нашем примере – с точностью до сотых. В каждом интервале две границы: нижняя и верхняя. Разность между верхней и нижней границей интервала равна шагу интервала h. Для первой группы нижняя граница интервала равна первому значению признака в ранжированном ряду. В нашем примере значение Хmin= 75,87 . Прибавляя к этому значению шаг интервала h , получаем верхнюю границу первой группы 75,87+7,62=83,49. Верхняя граница первого интервала является одновременно нижней границей второго интервала. Прибавляя к ней шаг интервала, определяем верхнюю границу второго интервала 83,49+7,62=91,11. Второй интервал в нашей задаче имеет границы 83,49 -91,11. Аналогично определим границы остальных интервалов и запишем их в графу 2 таблицы 1.5. Подсчет числа единиц в каждой группе проводится по ранжированному ряду. Если значение признака попадает на границу групп (например, первой и второй групп), то, как правило, единицу учитывают по верхней границе (в первой группе) по принципу «включительно». Результаты подсчета в нашем примере запишем в графу 3 табл.1.5. Табл.1.5. Интервальный ряд распределения квартир по цене 1 кв. м общей площади
Изобразим интервальный ряд распределения графически в виде гистограммы. Для построения гистограммы на оси абсцисс прямоугольной системы координат откладываем интервалы значений признака и на них строим прямоугольники с высотами, пропорциональными частотам интервалов (рис.1.3).  Вывод. Интервальный ряд распределения и его график показывают, что распределение квартир по ценовым группам неравномерное. Наиболее часто встречаются квартиры со значением признака в интервале 98,73 – 106,35 тыс. руб. за 1 м2. Наименьшее число единиц приходится на последний ценовой интервал. Распределение единиц по форме близко к нормальному распределению, так как именно средние цены имеют наибольшее распространение. Однако, первая, самая дешевая группа квартир также достаточно многочисленна. Задача 1.2. Построение ряда распределения по двум признакам. Условие. Имеются данные выборочного наблюдения за рынком строящегося жилья в Санкт-Петербурге: цена квадратного метра общей площади и удаленность квартиры от метро в минутах ходьбы. Требуется построить ряд распределения квартир одновременно по этим двум признакам. Решение. 1. Составим макет двумерного ряда распределения: количество строк будет соответствовать числу интервалов по первому признаку, а количество столбцов – числу количественных градаций второго признака. Границы интервалов по цене квадратного метра и значения признака пешей доступности метро (в минутах ходьбы) берем из задачи 1.1. 2. Определим в пределах каждого интервала численность квартир с соответствующим значением второго признака и запишем ее в таблицу 1.6. Табл. 1.6. Ряд распределения квартир по двум признакам.
3. Подсчитаем итоговые численности по строкам, графам и общий итог. Проверяем соответствие итогов по строкам данным интервального ряда распределения (табл.1.5), итогов по графам – данным дискретного ряда распределения (табл.1.3), общего итога - числу квартир в наблюдаемой совокупности. Вывод. Двумерный ряд распределения квартир по цене квадратного метра и по удаленности от метро показывает, что частоты концентрируются около диагональной прямой, соединяющей верхний правый и нижний левый углы таблицы. Это означает, что относительно дешевые квартиры сосредоточены в группах с максимальным удалением от метро и, наоборот, самые дорогие квартиры - в группах с минимальным удалением. Такое распределение дает основание выдвинуть предположение о наличии обратной связи между ценой 1 квадратного метра и расстоянием до метро. Задача 1.3. Расчет средней арифметической, моды и медианы в интервальном ряду распределения Условие: Имеются данные интервального ряда распределения квартир по цене 1 м2 общей площади (результаты решения задачи 1.1 в таб.1.5.) Требуется определить среднюю арифметическую, моду и медиану цены квадратного метра и сделать выводы. Решение. Составим макет таблицы 1.7 и перенесем в него исходные данные из таб.1.5.Табл. 1.7 Исходные и расчетные данные для определения средней арифметической величины, моды и медианы в интервальном ряду
А) Расчет средней арифметической величины проводится по формуле средней взвешенной:  , поскольку исходная информация представлена уже сгруппированными данными, и представленные группы имеют разную частоту встречаемости. , поскольку исходная информация представлена уже сгруппированными данными, и представленные группы имеют разную частоту встречаемости. а) За индивидуальные значения признака (Хi) в интервальном ряду условно принимаем серединные значения интервалов, которые определяем как полусумму значений нижней и верхней границ интервалов . Например, Х1 = В соответствии с правилом выбора весов*,статистическим весом или частотой (fi) при расчете средней цены за 1 м2 (тыс.руб./м2) должно быть не число квартир, а общая площадь. Тогда при умножении Хiна fi мы будем получать стоимость всей площади. В приложении 1 представлена база данных по выборке анализируемой совокупности квартир, отсортированная по цене. В программе Excel находим суммарные площади квартир, составляющих одну ценовую группу, и записываем их в табл.1.7 (графа 2). б) Найдем произведение вариант (Хi) на частоту (fi) и сумму этих произведений (итог графы 4). в) Рассчитаем среднюю арифметическую взвешенную величину по формуле:  Вывод: Средняя цена одного квадратного метра общей площади квартир в изучаемой совокупности составляет 98,16 тыс.руб. -------- * Правило выбора статистического веса при расчете средней величины: «Если осредняется абсолютная величина, то весом будет число единиц с данным значением признака. Если же осредняется относительная величина, то весом будет знаменатель относительной величины.» Примечание: средняя арифметическая по данным интервального ряда (98,16) незначительно отличается от средней, определенной по данным ранжированного ряда (6650,33÷68=97,8). Расхождение обусловлено тем, что в интервальном ряду расчеты проводились по усредненным значениям Хiв каждом интервале, а не по конкретным Х i . Б) Определим модальное значение признака (ХMO) в интервальном ряду расчетным и графическим способом. Расчетный(интерполяционный) метод Модальное значение определяется поэтапно: сначала определяется модальный интервал, а затем по формуле в нем находится Хmo. а) Определяем модальный интервал. Модальным будет интервал с наибольшей частотой встречаемости признака. В нашем примере модальный интервал (98,73 –106,35) , так как он имеет максимальную частоту встречае6мости - 1374,8 м кв. б) Вычисляем модальное значение признака, для чего используем формулу x0 --начальное значение модального интервала fmo -частота модального интервала fmo-1 - частота интервала, предшествующая модальному интервалу. fmo+1 - частота интервала, следующего за модальным интервалом. h -шаг интервала хмо Графический метод С этой целью используется гистограмма распределения. а) Определим модальный интервал, т.е. столбик гистограммы с наибольшей высотой. 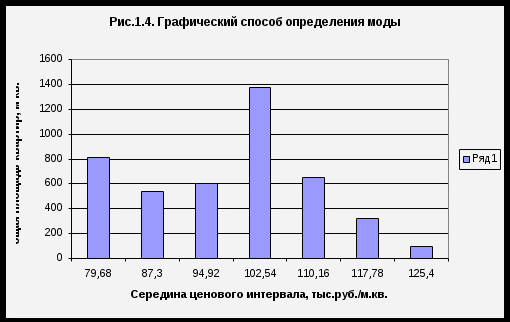 б) Точку, соответствующую верхней границе модального интервала, соединяем отрезком прямой с точкой, соответствующей верхней границе предыдущего перед модальным интервала. Точку, соответствующую нижней границе модального интервала, соединяем с точкой, соответствующей нижней границе интервала, последующего за модальным. Из точки пересечения прямых опускаем перпендикуляр на ось абсцисс и фиксируем модальное значение признака. Искомая точка на графике соответствует модальному значению – 102.66 (тыс. руб./м2). Вывод: Наиболее часто в изучаемой совокупности встречается цена 106,22 тыс. руб./м2. Расчет медианы в интервальном ряду : Расчетный (интерполяционный) метод Определение медианы в интервальном ряду по алгоритму схоже с определением модального значения: сначала определяется медианный интервал, а затем в нем по формуле рассчитывается конкретное значение медианы. а) Для определения медианного интервала для каждого интервала определим накопленную частоту (таб.1.7, графа 5). Накопленная частота покажет последний порядковый номер единицы для данной группы. Установим адрес медианы, то есть ее порядковый номер в ранжированном ряду, по формуле nмe = б) Рассчитаем медианное значение признака внутри медианного интервала по формуле: 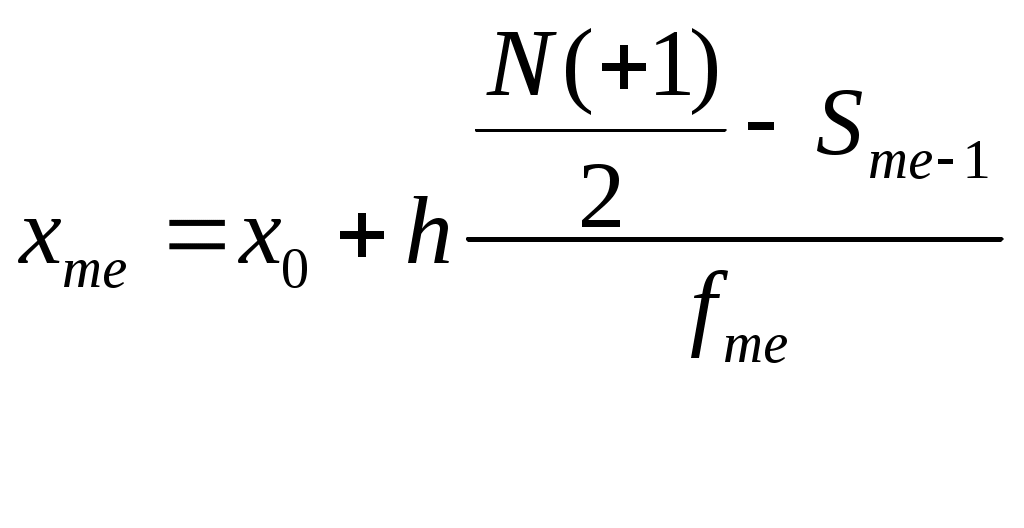 , , где x0 - начальное значение медианного интервала h -шаг интервала N - общее число единиц совокупности(+1) – используется в рядах с нечетным числом единиц совокупности Sme-1 – накопленная частота до медианного интервала fme - частота медианного интервала. Подставив необходимые величины в формулу, получаем Графический метод: Применение аналогично рассмотренному выше примеру дискретного ряда с тем различием, что за варианты принимаются верхние границы интервалов. а) Изобразим ряд распределения графически в виде кумулятивной кривой (рис.1.5) На оси абсцисс отмечаем точки, соответствующие верхним границам интервалов, на оси ординат – накопленные частоты. Накопленная частота покажет, сколько единиц совокупности имеет значение признака, не выше данного .Точки соединяем отрезками прямой. б) Из максимальной точки кумуляты (4401), соответствующей общему числу единиц, опускаем перпендикуляр на ось абцисс, делим перпендикуляр пополам и из точки деления проводим горизонтальную линию до пересечения с кумулятой. Далее из точки пересечения с кумулятой опускаем перпендикуляр на ось ОХ. Точка пересечения на оси ОХ указывает значение медианы, равное 100,07 тыс. руб. 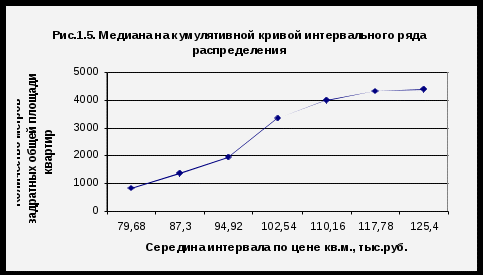 Вывод: половина всех площадей квартир продается по цене 100,07 тыс.руб. и менее за квадратный метр , другая половина – 100,07 тыс.руб. и более. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
