Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
 Скачать 2.09 Mb.
|
Задача 1.4. Исчисление показателей вариации в интервальном рядураспределенияУсловие: имеются данные интервального ряда распределения квартир по цене квадратного метра общей площади (см. табл. 1.5.)Требуется определить показатели вариации. Дисперсию вычислить по основной и рабочей формулам. Решение. 1.Определим размах вариации на основе ранжированного ряда распределения (табл. 1.4): R=Xmax - Xmin = 129,2 – 78,87 = 53,33 (тыс.руб./м2) Вывод: В изучаемой совокупности квартир максимальные различия в цене 1м2 составляют 53,33 тыс.руб. 2. Для определения средних показателей вариации заполним расчетную таблицу 1.8. Вычислим среднее линейное отклонение по формуле L=  где xi - значение признака,  - средняя арифметическая, , fi- частота встречаемости признака в совокупности.а) определим абсолютное отклонение каждой варианты от средней  =98,16 тыс.руб./м2 (графа 3);б) определим абсолютное отклонение, взвешенное соответствующими частотами, и их сумму (графа 4); в) рассчитаем среднее линейное отклонение L =  =  Вывод : среднее отклонение признака от средней величины составляет 10,36, т.е. в среднем по всем наблюдениям цена 1 квадратного метра отклоняется от средней цены на 10,36 тыс.руб.. 3.Исчислим дисперсию по основной формуле  а) вычислим квадраты отклонений индивидуальных значений варьирующего признака от средней величины (графа 5); б) определим взвешенные частотами квадраты отклонений и их сумму (гр. 6). в) вычислим дисперсию 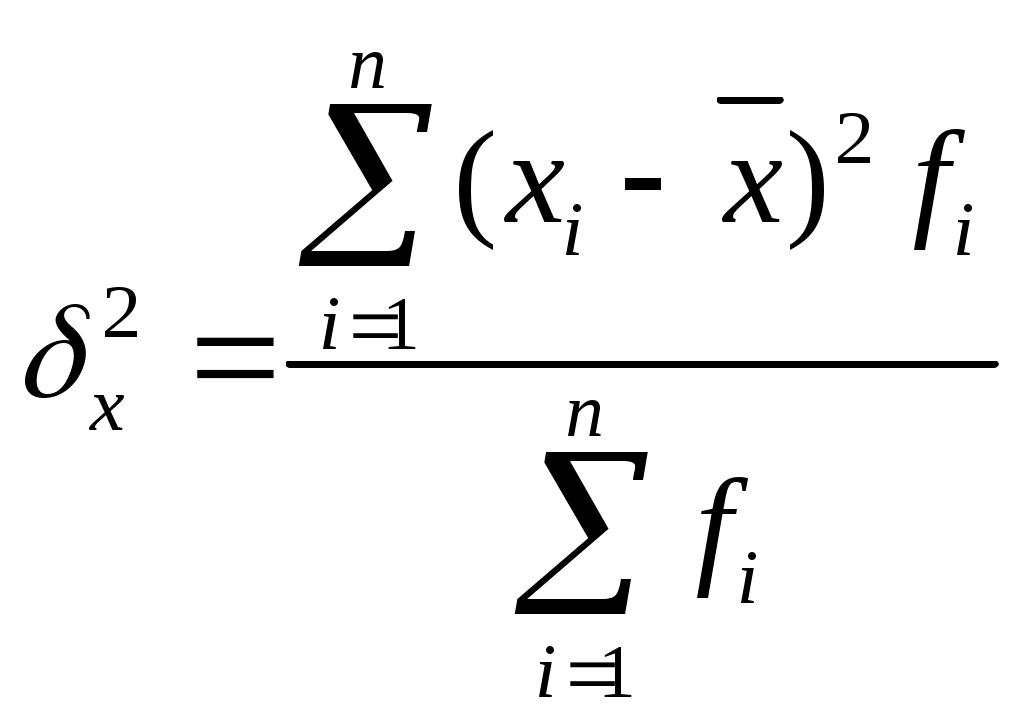 = 4. Определим дисперсию по рабочей формуле:  а) найдем квадраты значений признака (графа 7); б) рассчитаем взвешенные частотами квадраты значений признака и их сумму (графа 8); в) вычислим дисперсию  = 5. Рассчитаем среднее квадратическое отклонение как корень квадратный из дисперсии:  = Вывод: среднее квадратическое отклонение показывает, что все варианты отклоняются от средней величины в среднем на 12,27 тыс. руб./м2. Определим далее относительные характеристики вариации. 6. Коэффициент осцилляции  =  Вывод: относительная колеблемость крайних значений цены квадратного метра невысокая. 7.Относительное линейное отклонение  = Вывод: средняя колеблемость цены квадратного метра низкая и составляет 10,55 %, что свидетельствует об однородности совокупности. 8. Определим коэффициент вариации:  = Вывод: Коэффициент вариации показывает, что колеблемость признака в данном ряду распределения невысокая (менее 33 %) , и совокупность квартир является однородной по цене квадратного метра общей площади. Компьютерная реализация задачи Статистические характеристики варьирующих признаков, наиболее часто используемые в анализе, могут быть определены по первичной базе данных в программе Excel. Для этого в верхней строке выбираем «Вставка»,затем «Функция». В появившемся диалоговом окне следует указать категорию функций «Статистические», а затем среди предлагаемых опций выбираем необходимую статистическую характеристику: срзнач (средняя арифмети-ческая), мода, медиана, диспр(дисперсия признака). Далее выделяем столбец (или строку), содержащий индивидуальные значения интересующего нас признака по каждой единице совокупности, и на экран выводится значение соответствующей статистической характеристики. Так, по первичной базе данных (приложение 1), в программе Excel мы рассчитываем цену 1 м2 делением стоимости квартиры на ее площадь, а затем с помощью предлагаемых опций находим статистические показатели: средняя арифметическая  =97,8;мода хмо=100,0; медиана хме=100,0; дисперсия  =151,50.Небольшие расхождения с нашими расчетами связаны с тем, что в программе Excel расчеты проводятся по первичной базе данных, в то время как в нашем примере расчеты проводились по уже сгруппированным данным (по интервальному ряду распределения), где для всех единиц одной группы принимались значения признака, равные середине интервала.
Задача 1.5. Расчет средней арифметической и дисперсии альтернативного признака. Условие: из 68 наблюдаемых квартир 20 квартир имеют цену квадратного метра менее 90 тыс. руб. Требуется : определить среднее значение альтернативного признака и его дисперсию. Решение. Вариация альтернативного признака заключается в том, что одни единицы обладают данным признаком, а другие – нет. В нашем примере ряд квартир имеет цену квадратного метра менее 90 тыс.руб., а другие – более 90 тыс.руб. Обозначим наличие альтернативного признака через 1, а его отсутствие - через 0; долю единиц, обладающих признаком - р, а долю единиц, не обладающих признаком -g. Построим ряд распределения квартир по альтернативному признаку. Табл.1.9. Распределение квартир по альтернативному признаку
Поскольку частота встречаемости относительно дешевых и дорогих квартир неодинакова, то для расчета средней величины необходимо использовать формулу средней арифметической взвешенной: 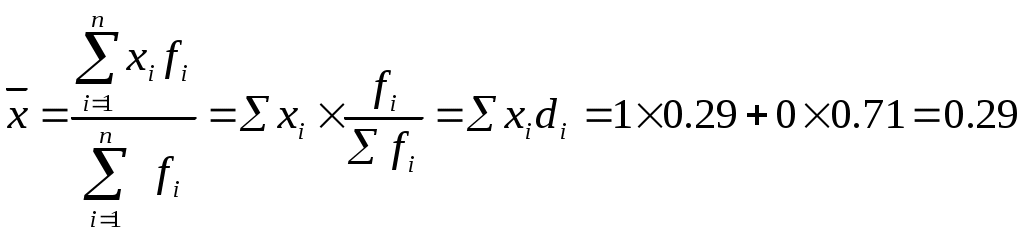 Мы видим, что средняя величина альтернативного признака равна его доле. Рассчитаем дисперсию альтернативного признака:   Учитывая, что p+g=1, а 1-p=g, имеем:  g2p+p2g=pg(g+p)=pgМы доказали, что дисперсия альтернативного признака равна произведению его долей. Следовательно, в нашем случае, дисперсия доли относительно дешевых квартир составит  **- прикладной аспект использования средней величины и дисперсии альтернативного признака будет рассмотрен позднее в задаче «Точечная и интервальная оценка параметров генеральной совокупности». Задача 1.6. Правило сложения дисперсий (разложения объемов вариаций) |
f