Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
 Скачать 2.09 Mb.
|
|
Вычислим выборочные дисперсии:  ;  4. Определим обобщенную среднюю ошибку двух выборочных средних: 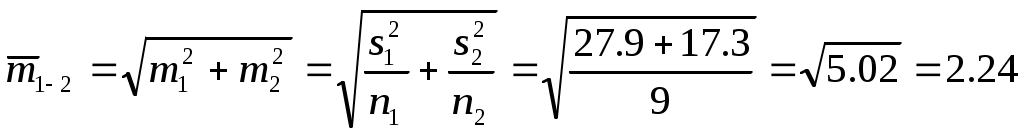 (тыс.руб.)5. Рассчитаем фактическое значение критерия t: tфакт. =  6. Табличное значение критерия определяется с учетом формирования независимой выборки (см. приложение 5). Численности выборок равны. Выясним, равны ли дисперсии в генеральных совокупностях. С этой целью проведем проверку гипотез по критерию F- распределения. Н0 :  ; ( в генеральных совокупностях дисперсии равны); НА:  .Фактическое значение критерия Фишера определяется как отношение двух выборочных дисперсий: Fфакт.=  где s12>s22 ; Fфакт.=  . Табличное значение критерия Фишера F  (при  и числе степеней свободы 9 и 9) равно 3,18. Так как фактическое значение критерия меньше табличного, следовательно, мы принимаем нулевую гипотезу о равенстве генеральных дисперсий: .Найдем по таблице критических значений двухстороннего критерия t - Стьюдента (приложение 2) значение t при уровне значимости 0,05 и числе степеней свободы v = 2·9 -2=18-2=16 : t0,05=2,12. 8. Сделаем статистически значимый вывод: поскольку tфакт.> t0,05 (4,12>2,12), нулевую гипотезу о равенстве средних в генеральных совокупностях отвергаем. Следовательно, принимаем альтернативную гипотезу о том, что средние в генеральных совокупностях не равны с вероятностью ошибки суждения 5%. 9. Сформулируем практически значимый вывод: различие выборочных средних не является случайным. Следовательно, цены за квадратный метр общей площади квартир в новостройках Калининского и Красносельского районов достоверно различаются: жилье в Калининском районе является более дорогим. Ошибка суждения составляет 5%. 2.2.2. Выборки независимые с разной численностью (  ),дисперсии генеральных совокупностей не равны ( )Условие: имеются выборочные данные о цене квадратного метра общей площади квартир в новостройках Калининского района и района Юго-Запад Санкт-Петербурга (табл.2.4). Требуется проверить статистическую гипотезу относительно равенства (неравенства) средних цен на жилье в этих районах. Уровень значимости 0,05. Решение. Сформулируем нулевую и альтернативную гипотезы: Н0:  Средние цены за 1 м2 в Калининском и Юго-Западном районах одинаковы, а различия выборочных средних обусловлены случайностями отбора.НА:  Средние цены за 1 м2 в Калининском и Юго-Западном районах различны.Таблица 2.4. Цены на жилье в новостройках Санкт-Петербурга
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
