Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки

• Название: Методические указания по решению типовых задач Учебнометодическое пособие для направления подготовки
• Дата: 14.10.2022
• Размер: 2.09 Mb.
• Имя файла: uch-met_posobie_statistika-metod_ukazania_po_resheniyu_tip_zadac.doc
• Тип: Методические указания; #734355
• страница: 5 из 20

Условие: имеется первичная база данных о рынке строящегося жилья в Санкт-Петербурге (приложение 1).

Требуется: используя закон разложения вариации, определить силу влияния района города на цену квадратного метра общей площади квартиры.

Решение. Для того, чтобы использовать закон разложения вариации в целях факторного анализа, сначала следует отсортировать первичную базу данных в программе Excel по величине факторного признака - району города (столбец х₂), а затем найти сводные данные и средние значения результативного признака (цены 1 м²) по каждой группе. Результаты сводки отсортированных данных представлены в табл.1.10.

Табл. 1.10. Группировка квартир по району города и сводка данных

Район города	Число наблюдений (квартир) - п	∑х1 – сумма индивидуальных значений результативного признака (цены 1м2)	Средняя цена 1 м2 в группе, тыс.руб. ( )
1 – Приморский, Выборгский	37	3434,76	94,45
2 - Калининский	10	1090,57	109,06
3 – Юго-Запад	11	1126,89	102,44
4 - Красносельский	10	938,11	93,81
Итого по всем наблюдениям	68	6650,33	97,80

Теорема сложения дисперсий говорит о том, что при сгруппированных единицах совокупности дисперсия общая ( _общ) равна сумме межгрупповой ( _мгр) и средней из внутригрупповых дисперсий ( _внтр).

_{общ = мгр + внтр}

Каждая из дисперсий рассчитывается как отношение объемов вариации к численности единиц совокупности :

Поскольку знаменатели дробей равны между собой, равенство справедливо также для числителей, т.е. общий объем вариации равен сумме межгруппового и внутригруппового объемов вариации. Таким образом, на первом этапе расчетов докажем равенство объемов вариаций, на втором – равенство дисперсий.

1. Для расчета объемов вариаций необходимо определить общую среднюю по совокупности и групповые средние по каждой группе.

Общая средняя величина по совокупности равна: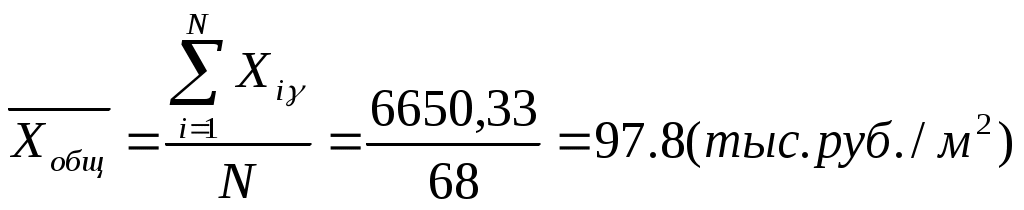

.

Групповые средние равны:

;



Полученные значения запишем в последнюю графу таблицы 1.10.

2. По смысловой формуле общий объем вариации представляет собой сумму квадратов отклонений всех 68 отклонений индивидуальных значений признака от общей средней:

= (81,31-97,8)²+(75,96-97,8)²+…(98,03-97,8)²=10302^*
Межгрупповой объем вариации :

=(94.45-97.8)² ·37 + (109.06-97.8)² ·10 +

+(102.44-97.8)²·11=(93.81-97.8)²·10 =2078
*Расчеты выполнены в программе Excel

Для расчета внутригруппового объема вариации по совокупности в целом предварительно определим внутригрупповой объем вариации в каждой группе. Объем вариации для первой группы равен сумме тридцати семи квадратов отклонений ( по числу наблюдений в первой группе):

=(481,31-94,45)²+(75,96-94,45)²+…= 5876,05

Объем вариации во второй группе составляет сумму десяти квадратов отклонений:

= (103,92-109,06)²+(103,98-109,06)²+…=251,07

Аналогично объем вариации в третьей и четвертой группах равен:

=(89,96-102,44)²+(90,14-102,44)²+…=1941,23;

= (88,97-93,08)²+(89,00-93,8)²+…=155,65

Складывая W_вн.1 , W_вн.2 , W_вн.3 и W_вн.4 , получаем внутригрупповой объем вариации по всей совокупности:

W_вн.= W_вн.1 + W_вн.2 + W_вн.3 +, W_вн.4 =5876,05+251,07+1941,23+155,65=8224

Рассчитанные показатели доказывают справедливость равенства объемов вариации W_общ. = W_межгр. + W_внутр

10302 = 2078 + 8224

3. Для расчета дисперсий необходимо разделить объемы вариаций на численность совокупности
= ;
151,5 = 30,56 + 120,94
4. Для оценки связи вариации цены квадратного метра с группировочным признаком (районом города) рассчитаем эмпирический коэффициент детерминации как отношение межгрупповой дисперсии к общей дисперсии: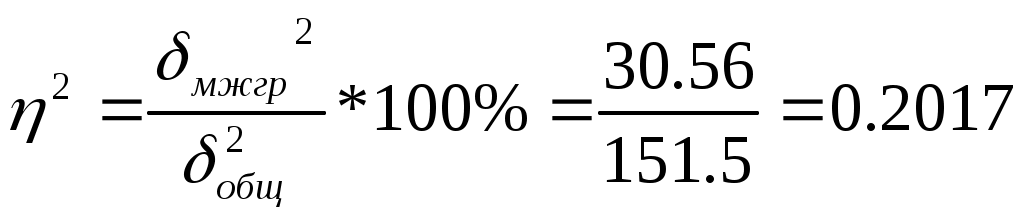



Вывод: коэффициент детерминации показывает, что 20,17 % вариации цен за квадратный метр общей площади в данной совокупности наблюдаемых квартир было обусловлено районом города, а 79,83 - другими ценообразующими факторами.

Эмпирическое корреляционное отношение равно η =

По предложенной Чэддоком шкале значение 0,45 в задаче свидетельствует об умеренном влиянии фактора района на цену квадратного метра.
Шкала Чеддока

η	0,1-0,3	0,3-0,5	0.5-0,7	0,7-0,9	0,9-0,99
влияние	слабое	умеренное	заметное	сильное	очень сильное

Вопросы для проверки знаний по модулю 1:

1. Что такое статистическая совокупность?

2. В чем отличие признаков дискретных и непрерывных?

3. Какие виды рядов распределения вы знаете?

4. Что такое ранжированный ряд распределения?

5. Постройте график ранжированного ряда, если известно, что совокупность имеет пять единиц и вариация признака равна нулю.

6. Как называется графическая форма ранжированного ряда и как она выглядит?

7. Каково содержание колонок в дискретном вариационном ряду?

8. Что откладывается на координатных осях при построении полигона распределения?

9. По каким признакам чаще всего строится интервальный вариационный ряд?

10. Как определить число интервалов при построении интервального ряда распределения?

11. Как определить шаг интервала?

12. Как определить границы интервалов?

13. Что откладывается на координатных осях при построении гистограммы распределения?

14. Напишите формулу средней арифметической взвешенной.

15. Дайте определение моды.

16. Что показывает медиана?

17. Как найти медиану в интервальном ряду распределения?

18. Назовите показатели вариации.

19. Напишите формулу дисперсии.

20. Что произойдет с дисперсией признака, если все значения признака

одновременно уменьшить на 10 и увеличить в 2 раза?

21. В партии продукции на некачественную продукцию приходится 10 %. Определить коэффициент вариации.

22. Какой показателей вариации может быть использован для сравнения вариации нескольких признаков? Почему?

23. Определить объем вариации, если среднее квадратическое отклонение равно 5, а совокупность состоит из 4-х единиц.

24. Какие показатели характеризуют среднюю колеблемость признака в совокупности?

25.Сформулируйте закон разложения вариации.

26. Как рассчитать эмпирическое корреляционное отношение?

27. Во сколько раз межгрупповая вариация меньше внутригрупповой, если корреляционное отношение равно 0,25?

Модуль 2. Выборочный метод. Проверка статистических гипотез.

Целью изучения модуля 2 является освоение на практике возможностей выборочного метода: способов формирования выборочной совокупности и научных подходов к оценке параметров генеральной совокупности по данным выборки на основе точечной и интервальной оценки, а также проверки различных статистических гипотез.

Вопросы:

1. 
   Сущность выборочного метода и способы формирования выборки;
   
2. 
   Точечная и интервальная оценка параметров генеральной совокупности по данным большой и малой выборок;
   
3. 
   Проверка статистических гипотез относительно средних величин по данным 2-х выборок по критерию t-Стьюдента при различных условиях формирования выборок;
   
4. 
   Проверка гипотез относительно средних величин по результатам нескольких выборок по критерию F-Фишера;
   
5. 
   Конкретизация результатов дисперсионного анализа на основе метода контрастов Шеффе.
   

Методические указания

Получение обобщающих характеристик статистической совокупности возможно на основе изучения всей совокупности, или же ее части. Второй способ, получивший название несплошного наблюдения, предпочтителен при ограниченности времени или ресурсов на исследование, а в ряде случаев является единственно приемлемым. Среди способов несплошного статистического наблюдения (изучение основного массива, выборочное наблюдение, монографическое наблюдение) основным является выборочное наблюдение, так как оно наиболее разработано с математико-статистической точки зрения.

Выборочное наблюдение – это наблюдение за специально отобранной из исходной статистической совокупности частью единиц с целью получения полных и объективных характеристик всей совокупности.

Введем основные понятия выборочного метода.

Генеральная совокупность – это исходная статистическая совокупность, по которой должны быть получены статистические характеристики (параметры). Выборочная совокупность (выборка) –это специально отобранная часть генеральной совокупности. Предназначение выборки – быть надежной моделью генеральной совокупности с точки зрения статистических параметров. Оценка – это статистическая характеристика (параметр) выборочной совокупности, на основе которой делается заключение относительно той или иной характеристики генеральной совокупности.

Поскольку выборка, как правило, составляет весьма незначительную часть генеральной совокупности, то следует предположить, что выборочная оценка будет отличаться от искомого генерального параметра. Эти различия получили названия ошибок отображения или ошибок репрезентативности. При организации выборочного метода стоит задача минимизации ошибок.

Статистическая оценка означает, что выводы относительно статистических параметров (средней, дисперсии, коэффициента вариации) генеральной совокупности делаются на основе изучения выборочных данных. Исследуемый параметр генеральной совокупности при этом может быть охарактеризован одним числом (точечная оценка), либо указывается интервал, в котором он находится с определенной вероятностью (интервальная оценка). Как точечная, так и интервальная оценка предполагают, что сначала значения соответствующих параметров определяются по выборке. Такие значения носят название оценок.

При точечной оценке параметра генеральной совокупности, например, средней величины , его значение приравнивается к оценке , но в силу того, что оценка средней величины определена с использованием случайно сформированной выборки, она (оценка) обязательно должна быть дополнена показателем ее средней ошибки ( ). Алгоритм расчета средней ошибки зависит от того, для какого параметра она рассчитывается. В итоге результаты точечной оценки средней величины признака в ге­неральной совокупности записываются следующим образом: со средней ошибкой .

При интервальной оценке параметра генеральной совокупности (например, средней величины) так­ же, как и при точечной, сначала необходимо определить его значение по выборке, т.е. оценку . Значение оценки принимается за центр интервала. Далее устанавливается величина случайной предельной ошибки оценки , на основе которой и устанавливаются границы интервала. В нем с некоторой гарантией (доверительным уровнем вероятности) находится значение исследуемого параметра в генеральной совокупности. Следовательно, интервальная оценка среднего значения признака в генеральной совокупности предполагает следующую запись: или -

где - - нижняя граница доверительного интервала для средней;

+ - верхняя граница доверительного интервала для средней.

При расчете предельных значений ошибки используется формула:

= , где - средняя ошибка выборочной оценки средней величины ; t_р - коэффициент ( нормированное отклонение ), зависящий от доверительного уровня вероятности того , что исследуемый параметр генеральной совокупности не выйдет за установленные границы интервала. Отсюда следует, что для расчета предельной ошибки вначале следует найти среднюю ошибку оценки, затем определиться с доверительным уровнем вероятности р, и в зависимости от его величины использовать соответствующий коэффициент.

В практических исследованиях наиболее часто используют следующие доверительные уровни вероятности: 0,90; 0,95; 0,99; 0,999. Выбор гарантии вывода зависит от степени ответственности решаемой задачи: чем выше ответственность, тем выше должен быть доверительный уровень вероятности.

Порядок нахождения коэффициента (нормированного отклонения) зависит также от численности выборки, которая используется для статистической оценки параметра генеральной совокупности. При n 30 коэффициент определяется из таблицы « Значение интеграла вероятностей при разных значениях t», так как ошибки оценок при выборках численностью более 30 единиц распределяются в соответствии с законом нормального распределения * (приложение 2), и его величина зависит только от доверительного уровня вероятности. При численности выборки менее 30 единиц следует воспользоваться таблицей «Значение двухстороннего критерия t –Стьюдента» (приложение 3), где значение коэффициента зависит не только от доверительного уровня вероятности, но и от численности выборки (степеней свободы вариации).

Другой областью применения выборочного метода является проверка разнообразных статистических гипотез относительно тех или иных свойств генеральных статистических совокупностей: законов распределения, параметров распределения. С этой целью необходимо выдвинуть так называемую нулевую гипотезу (Н₀). Решение о принятии или отказе от нулевой гипотезы должно быть основано на сопоставлении фактического значения того или иного математического критерия (критерия t- нормального распределения, t - Стьюдента, F - распределения, и др.) с его критическим (табличным) значением. Выбор математического критерия определяется характером решаемой задачи, а также объемом выборки. В результате проверки по данным выборок нулевую гипотезу следует принять, если фактическое значение критерия попадает в область допустимых значений критерия. Если же оно попадает в критическую область, от нулевой гипотезы следует отказаться.

Проверка статистических гипотез относительно средних величин по данным двух выборок может быть проведена по параметрическому критерию t – Стьюдента (по малым выборкам п ‹ 30) или по критерию t- нормального распределения по выборкам достаточно большого объема (п ).

С целью проверки необходимо сформулировать нулевую гипотезу ( Н₀) относительно средних величин. Она может быть основана на предположении, что выборки взяты из генеральных совокупностей с равными средними величинами: Н₀: или Н₀: . Проверяемой (нулевой) гипотезе противостоит некоторая альтернативная гипотеза (Н_А), которая может быть сформулирована в общем виде как Н_А: .

Фактическое (выборочное) значение критерия рассчитывают следующим образом: t_факт. = , где - обобщенная средняя ошибка двух выборочных средних. Фактическое значение критерия необходимо сопоставить с критическим значением при заданном уровне значимости ( ). Если выборочное значение критерия попадает в критическую область

(t_факт. > ), нулевая гипотеза о равенстве средних должна быть отвергнута; если же выборочное значение критерия попадает в область допустимых значений (t_факт. ), нулевую гипотезу следует принять.

Нулевая гипотеза о равенстве средних в двух генеральных совокупностях может быть проверена путем сравнения разности между выборочными средними ( ) с предельной случайной ошибкой (наибольшее случайное различие - НСР) при заданном уровне значимости ( ). Если разность между выборочными средними находится в пределах НСР ( ), нулевую гипотезу следует принять. Если же разность между средними по выборкам выходит за пределы НСР ( ), нулевая гипотеза должна быть отвергнута.

В конкретных задачах при выборе алгоритма расчетов по критерию t – Стьюдента необходимо учитывать:

1. 
   схему формирования выборок (выборки независимые или зависимые);
   
2. 
   равенство или неравенство объемов выборок;
   
3. 
   равенство или неравенство дисперсий в генеральных совокупностях.
   

Так как выборочные дисперсии, как правило, неравны, в ходе проверки статистических гипотез относительно средних величин в двух генеральных совокупностях необходимо проверить гипотезу относительно их дисперсий при помощи критерия F - распределения. Допустим, что нулевая и альтернативная гипотезы сформулированы следующим образом:

Н₀: и Н_А: .

Для проверки нулевой гипотезы о равенстве дисперсий в генеральных совокупностях следует определить фактическое (выборочное) значение критерия F как отношение выборочных дисперсий F_факт.= где s₁²>s₂²) и сравнить его с критическим значением при заданном уровне значимости (F ). Если фактическое значение критерия попадает в область допустимых значений (F_факт. F ), нулевая гипотеза о равенстве дисперсий в генеральных совокупностях принимается. Если же фактическое значение критерия попадает в критическую область (F_факт>_. ), от нулевой гипотезы следует отказаться.

В случае, когда дисперсии генеральных совокупностей неравны, число степеней свободы вариации определяется с учетом поправки: , где п₁ и п₂ - численности выборочных совокупностей, а s₁² и s₂² - дисперсии выборочных совокупностей.

Для оценки существенности различий нескольких средних в многовариантных сравнениях применяется особый алгоритм, получивший название дисперсионного анализа. Фактические имеющиеся данные по каждому варианту представляют собой отдельную выборку.

В основе дисперсионного анализа лежит закон разложения вариации (см. задачу 1.6). Сравниваемые варианты различаются между собой по какому-то факторному признаку (например: тип застройки, тип почвы, район и т.п.), а фактические данные по вариантам представляют собой значения результативного признака (например, цены 1 м² помещения, цены 1 сотки земельного участка и т.п.).

В ходе анализа мы сравниваем средние значения результативного признака по всем вариантам, выявляя их колеблемость вокруг общей средней. Эта межгрупповая вариация отразит, таким образом, влияние фактора на результат. Вариация результативного признака внутри одной выборки обусловлена действием всех прочих (остальных) факторов, кроме изучаемого, и называется остаточной вариацией. Действие этих причин носит разнонаправленный, случайный характер.

Общая схема дисперсионного анализа в его простейшем варианте сводится к следующим этапам:

1. Выдвигаем нулевую гипотезу о том, что средние значения результативного признака по т генеральным совокупностям равны между собой. Иными словами, мы предполагаем, что различия выборочных средних по вариантам носят случайный характер, то есть сформировались за счет случайного отбора наблюдений. Математическая запись нулевой гипотезы Н₀: . Альтернативная гипотеза , наоборот, предполагает, что имеются хотя бы две из имеющихся генеральных средних не равные между собой. Н_а = .

2. Устанавливаем уровень значимости , с которым будет приниматься одна из выдвинутых гипотез.

3. Рассчитываем среднее значение результативного признака по каждому варианту (выборочные средние) и общая средняя по всем вариантам , где i – порядковый номер варианта, j – порядковый номер наблюдения в каждом варианте, m- число сравниваемых вариантов, n – число повторностей (наблюдений) в каждом варианте. Для упрощения последующих рассуждений примем, что в каждой выборке имеет место одинаковое число наблюдений.

4. Устанавливаются источники вариации результативной переменной и определяется объем вариации по каждому источнику: общий объем вариации

; объем межгрупповой или факторной вариации ; объем внутригрупповой или остаточной вариации .

5. Для каждого из найденных объемов вариации находим соответствующее ему число степеней свободы вариации (degreesoffreedomили d.f.) : для общей вариации df_общ= mn-1; для факторной вариации

df_факт= m-1; для остаточной вариации df_ост=( mn-1) – (т-1).

6. Рассчитываем выборочные дисперсии как отношение объема вариации к соответствующему числу степеней свободы: ; . Данные дисперсии являются мерой влияния фактора или группы факторов на вариацию результативного показателя: чем сильнее влияние изучаемого фактора, тем выше факторная дисперсия; чем сильнее влияние прочих случайных причин, тем больше остаточная дисперсия.

7. Далее полученные дисперсии сравниваются на предмет того, какая из них больше. Если окажется что , то следует признать, что сила действия изучаемого фактора лежит в пределах влияния случайных причин. В этом случае мы признаем случайный характер расхождений между выборочными групповыми средними и без расчета критерия F-Фишера принимаем нулевую гипотезу о равенстве генеральных средних. Если же , то следует рассчитать отношение дисперсий, то есть по выборочным данным получить фактическое значение критерия Фишера: .

8. Полученное фактическое значение критерия сравнивается с его табличным значением (приложение 4). Табличное значение критерия покажет максимально возможное случайное расхождение двух выборочных дисперсий, если выборки произведены из одной генеральной совокупности. Его находят исходя из принятого уровня значимости и числа степеней свободы для факторной (столбец таблицы) и остаточной (строка таблицы) дисперсий. Если F_факт. F , то с установленной вероятностью ошибки принимается предположение, что превышение одной дисперсии над другой лежит в пределах случайных расхождений. Следовательно, выборки произведены из одной генеральной совокупности, и генеральные средние будут равны друг другу: нулевая гипотеза принимается. Иными словами, принимаем гипотезу об отсутствии существенных различий между сравниваемыми вариантами и об отсутствии влияния изучаемого фактора на результативный показатель. Если же F_факт>_. , то от нулевой гипотезы следует отказаться, принимается альтернативная гипотеза о том, что хотя бы две генеральные средние не равны между собой. В этом случае можно говорить, что фактор оказывает существенное влияние на результат.

Таким образом, вывод о справедливости нулевой гипотезы имеет место в двух случаях: а) если ; б) если F_факт. F . Альтернативная гипотеза о наличии различий хотя бы между двумя генеральными средними принимается только в одном случае - если F_факт> . Другими словами, принятие альтернативной гипотезы не дает основания считать, что переход от одной градации фактора к другой всегда приведет к существенному изменению величины результативного признака. Поэтому в большинстве случаев дисперсионный анализ требует дальнейшей конкретизации: какие именно средние (или варианты) не равны между собой? Универсальным методом попарного сравнения средних по результатам дисперсионного анализа является метод контрастов Шеффе (задача 2.3.2). Для случая, когда градации фактора носят качественный характер (то есть выражены словом – вид угодий, тип почвы, способ застройки, регион и т.п.) и численности выборок равны между собой, попарное сравнение средних может быть проведено на основе методики Хартли.