лабы информатика. Методические указания по выполнению лабораторных работ для студентов фэуб специальностей 080200 Менеджмент
 Скачать 10 Mb. Скачать 10 Mb.
|
|
Контрольные вопросы 1 Что означают понятия: а) ряд данных; б) категория ;в) легенда? 2 Сколько рядов данных может быть изображено на круговой диаграмме; на кольцевой диаграмме? З Как отредактировать на диаграмме: а) название диаграммы; б) названия осей Х и Y; в) легенду ; г) изменить тип диаграммы д) добавить новые данные 4 Как указать на гистограмме ключевые значения ряда данных? 5 Каким образом можно комбинировать разные типы диаграмм? 6 Как ввести вспомогательную ось? Задания 1 Исходные данные для л.р. №2 те же, что и для л.р. №1. 2 Построить в Excel график функции: y=n·sin(2x), -5 <= х <=5, шаг Δх = 1, где n – номер компьютера в аудитории. 3 Построить 4 двумерные и 4 трехмерные диаграммы любых типов, содержащих не менее 3 рядов данных (функций) для 5-6 значений категорий (аргумента функций). Виды функций взять из л.р №1. 4 Построить график изменения цены товара во времени согласно табл.1. Изменение цены товара Таблица 1
В графике использовать две оси ординат, на одной цена товара должна быть приведена в рублях, на другой – в долларах (с помощью диаграммы График(2 оси). 5 Изменить цвет осей, шрифт названий графика и осей, ввести сетку. 6 Дополнить таблицу ещё тремя значениями функции для трёх последующих месяцев и изменить согласно новым данным график функции ( с помощью команд меню Диаграмма). Содержание отчёта 1 Название, цель, содержание работы 2 Задание своего варианта 3 Письменные ответы на контрольные вопросы 4 Выводы по работе На дискете должны быть сохранены результаты работы Лабораторная работа №4 Прогнозирование с помощью регрессионного анализа Цель работы: научиться выполнять прогнозирование экономических параметров с помощью одномерного и многомерного регрессионного анализа Содержание работы: 1 Линейный регрессионный анализ. 2 Экспоненциальный регрессионный анализ. 3 Линейный многомерный регрессионный анализ Экономическая информация чаще всего представляется в виде таблиц. Например, в табл. 1 представлена зависимость прибыли У от рентабельности производства Х. Таблица 1
Если изобразить эти значения на графике, то получатся точки синего цвета - см. рис. 1. Однако, пользоваться таблицами для анализа данных сложно, т.к. нельзя точно определить, каким будет у при промежуточном значении х (напр., при х=2,35) или при х, выходящем за пределы таблицы (х < 0 и х > 5,01). Поэтому таблицу заменяют на уравнение, наиболее точно соответствующее табличным данным. Для табл. 1 такой функцией будет уравнение у = х 2,8+2 (сплошная линия на рис. 1). 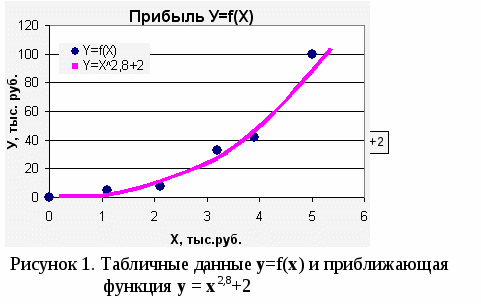 Эта функция называется приближающей функцией или уравнением регрессии. Пользоваться уравнением для анализа данных гораздо удобней, т.к. можно не только точно рассчитать значение функции у при любом аргументе х внутри таблицы (интерполяция), но и определить у при значении х, выходящем за пределы табличных данных (напр., при х = 8 тыс. руб. -экстраполяция), т.е. сделать прогноз изменения функции. Процесс замены таблицы на приближающую функцию называется регрессионным анализом. Табличный процессор Excel позволяет заменять таблицу на уравнения двух видов – линейное, в виде прямой линии у = m х + b (когда у зависит от х в первой степени) и экспоненциальное, в виде кривой линии у = bmX (когда у зависит от х не линейно). соответственно и регрессионный анализ называется линейным и экспоненциальным. Анализ является одномерным, если он проводится для функцииY у, зависящей только от одного аргумента х (т.е. у = f(х)). Если у зависит от нескольких переменных (у = f (х 1, х 1, …, х 1), то это многомерный регрессионный анализ. 1 Линейный регрессионный анализ Одним из методов, используемых для прогнозирования, является регрессионный анализ. Регрессия - это статистический метод, который позволяет найти уравнение, наилучшим образом описывающее совокупность данных, заданных таблицей. 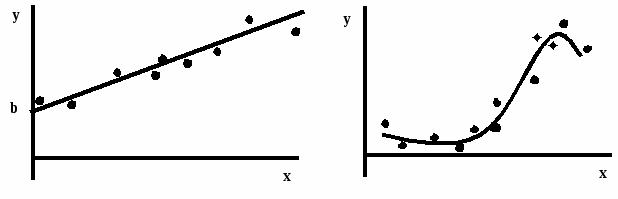 Рисунок 2 Линейная регрессия Рисунок 3 Нелинейная регрессия На графике эти данные отображаются точками. Регрессия позволяет подобрать к этим точкам кривую у=f(x), которая вычисляется по методу наименьших квадратов и даёт максимальное приближение к табличным данным. Линейная регрессия дает возможность наилучшим образом провести прямую линию через точки одномерного массива данных. Уравнение с одной независимой переменной, описывающее прямую линию, имеет вид: y=mx+b, (1) где: х - независимая переменная ; у -зависимая переменная; m – характеристика наклона прямой; b - точка пересечения прямой с осью у. Например, имея данные о реализации товаров за год с помощью линейной регрессии можно получить коэффициенты прямой (1) и, предполагая дальнейший линейный рост, получить прогноз реализации на следующий год. 2 Экспоненциальный регрессионный анализ Нелинейная регрессия позволяет подбирать к табличным данным нелинейное уравнение – параболу, гиперболу и др. Excel реализует нелинейность в виде экспоненты, т.е. подбирает кривую вида y=b·mx (2) которая позволяет наилучшим образом провести экспоненциальную кривую по точкам данных, которые изменяются нелинейно. Так, например, данные о росте населения почти всегда лучше описываются не прямой линией, а экспоненциальной кривой. При этом нужно помнить, что достоверное прогнозирование возможно только на участках подъёма или спуска кривой. Например, делать экспоненциальный прогноз для функции, изменяющейся синусоидально, можно только на участках подъёма или спуска функции, для чего её разбивают на соответствующие интервалы. 3 Множественная регрессия Множественная регрессия представляет собой анализ более одного набора данных аргумента х и дает более реалистичные результаты. Множественный регрессионный анализ также может быть как линейным, так и экспоненциальным. Уравнения регрессии (1) и (2) примут соответственно вид (3) и (4): у=mlxl + m2x2 + ... + mnxn + b (3) у = b·mlxl· m2x2 · ... · mnxn (4) где: xl, x2, ..., xn - независимые переменные. С помощью множественной регрессии, например, можно оценить стоимость дома в некотором районе, основываясь на данных его площади, размерах участка земли, этажности, вида из окон и т.д. Использование функций регрессии В Excel имеется 5 функций для линейной регрессии (ЛИНЕЙН(...), ТЕНДЕНЦИЯ(...), ПРЕДСКАЗ(...), НАКЛОН(...), СТОШУХ(...)) и 2 функции дня экспоненциальной регрессии - ЛГРФПРИБЛ(...) и POCT(...). Рассмотрим основные из них. 1 Функция =ЛИНЕЙН(изв._знач._y;изв. _знач. x;конст;стат) (5) вычисляет коэффициент m и постоянную b для уравнения прямой (1). Её аргументы: Известные_значения_y и известные_значения_x - это множество значений y и необязательное множество значений x (их вводить необязательно), которые уже известны для соотношения (1). Константа-это логическое значение , которое указывает требуется ли, чтобы константа b была равна 0 (т.е. линия проходит через начало координат и при х=0 у тоже равно 0). Если константа имеет значение ИСТИНА или опущено,то b ≠ 0 и вычисляется обычным образом. Статистика - это логическое значение, которое указывает, требуется ли вывести дополнительную статистику по регрессии. Результат выполнения функции зависит от значения аргумента статистика. Если статистика имеет значение ЛОЖЬ(или 0),то функция ЛИНЕЙН возвращает только значения коэффициентов m и b, в противном случае выводится дополнительная регрессионная статистика в виде табл.2: Таблица 2
|
