Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Определение коэффициента трения каченияЦель работы: определить коэффициент трения качения цилиндра по плоскости для различных пар металлических поверхностей и определить момент инерции сложной системы методом колебаний Т 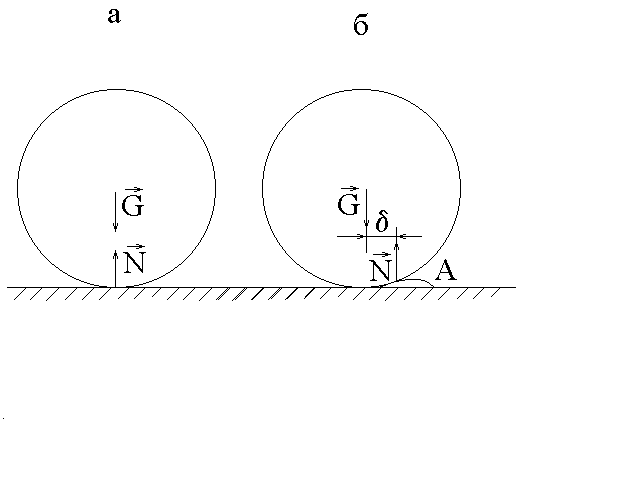 Рис.1 еоретическое описание Рассмотрим цилиндр, покоящийся на горизонтальной плоскости (рис.1,а). На него действуют две взаимно уравновешивающие силы: сила тяжести  , где m – масса цилиндра, и нормальная реакция плоскости  . Если цилиндр (колесо) катится по плоскости, то появляется трение качения. Можно выделить следующие причины его возникновения. И цилиндр и плоскость при качении деформируются. При этом происходят потери механической энергии, связанные: а) с работой, затрачиваемой на образование валика А деформированной плоскости перед катящимся цилиндром (рис.1,б); б) со сжатием плоскости перед катящимся; в) с преодолением мостиков сцепления – тех областей на поверхности соприкосновения цилиндра и плоскости, где из-за неровности поверхностей существуют настолько большие давления, что между молекулами цилиндра и плоскости возникают силы межмолекулярного притяжения и они в этих местах "сцепляются" друг с другом.Эти три причины приводят к тому, что точка приложения нормальной реакции  с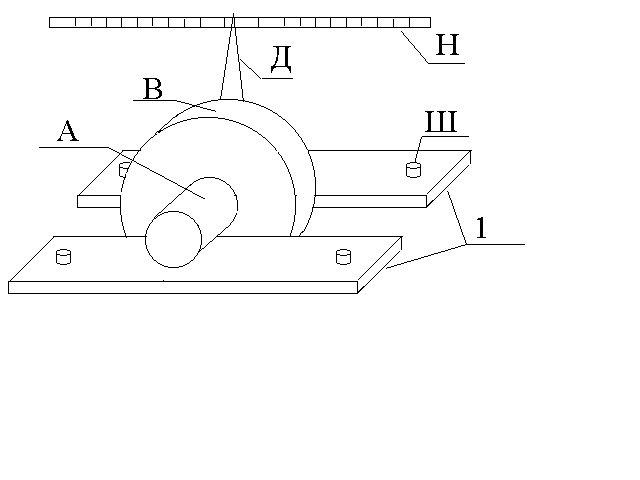мещается на расстояние , в результате возникает момент силы реакции, направленный по оси вращения, которая проходит перпендикулярно плоскости рисунка 1, и препятствующий качению цилиндра. Модуль этого момента (1)П  Рис.2 оэтому Mk называют моментом сопротивления качению, а величину , численно равную смещению точки приложения реакции плоскости 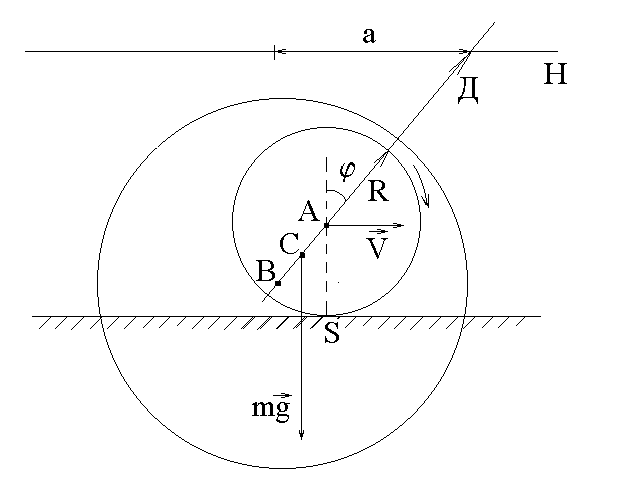– коэффициентом трения качения. Коэффициент трения качения измеряется в единицах длины и, как показывает опыт << R (R – радиус цилиндра). Рис.3 В работе используются два жестко скрепленных цилиндра А и В с несовпадающими параллельными осями. Они могут вращаться на горизонтально расположенных образцах 1 различных металлов (рис.2) вокруг оси цилиндра А радиусом R. Стрелка Д, прикрепленная к цилиндру А, фиксирует на шкале Н линейное смещение колеблющейся системы от положения равновесия. Ш – штырьки для удержания образцов. Так как оси цилиндров А и В не совпадают, то центр масс системы С находится на линии АВ на расстоянии  от оси цилиндра А (рис.3). Момент силы тяжести  стремится вернуть систему в положение равновесия и при малых углах поворота ( ) пропорционален смещению из положения равновесия . Это является условием гармонических колебаний, которые будет совершать система относительно положения равновесия = 0 (стрелка Д отклоняется то в одну сторону, то в другую сторону от положения О на шкале Н).Из-за действия диссипативных сил трения колебания системы будут затухать. Определим уравнение этих колебаний. Запишем уравнение динамики вращательного движения системы относительно мгновенной оси вращения, проходящей через точку S касания цилиндра А с плоскостью перпендикулярно плоскости рисунка 3. Кроме момента силы тяжести действует момент сопротивления качению на цилиндр (1). Величина коэффициента трения качения пропорциональна скорости V катящегося без проскальзывания цилиндра А. Если учесть связь линейной и угловой скорости цилиндра:  , то , (2)и из формулы (1)  .Тогда уравнение динамики имеет вид  (3)где J – момент инерции системы относительно мгновенной оси вращения S; знаки в уравнении (3) показывают, что моменты сил препятствуют увеличению угла отклонения . П Рис. 3 ри малых углах ( ) это уравнение аналогично динамическому уравнению затухающих колебаний: , (4)где  , (5) . (6)Поэтому угол отклонения стрелки Д от положения равновесия изменяется по закону  , (7)где  – (8)частота затухающих колебаний;  – угол отклонения стрелки в начальный момент времени. Колеблющаяся таким образом система является разновидностью физического маятника.Совершив n полных колебаний за время t = nT (T – период колебаний), стрелка отклонится на угол φn (φn < φ0). Так как линейное смещение a стрелки Д вдоль шкалы Н пропорционально углу поворота стрелки , то из (7) следует, что  откуда получим  .Величину  (9)называют логарифмическим декрементом затухания, следовательно  (10)Подставляя выражения (6) и (10) в формулу (8) и учитывая, что  , находим формулу для определения момента инерции J системы относительно мгновенной оси вращения S: (11)Из формул (5), (10) и (11) определим выражение для k:  (12)В данной работе можно лишь приближенно оценить коэффициент трения качения. Для этого воспользуемся формулами (2) и (7). Найдем производную  :  Максимальная скорость движения центра цилиндра Aдостигается при нулевом угле отклонения . Это условие выполняется, когда  ( ). Для упрощения вычислений можно положить  (амплитуда слабо уменьшается за время первого колебания).Тогда  Таким образом, максимальную скорость качения цилиндра, а также оценку для коэффициента трения качения можно описать следующей формулой 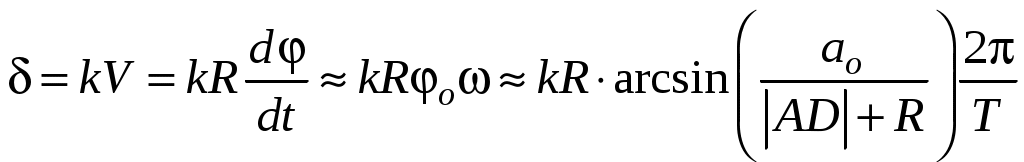 (13)Под цилиндр А подкладывают плоские пластинки из различного материала, что позволяет определить коэффициенты трения цилиндра для различных пар (цилиндр-пластинка) и сравнить полученные результаты. Закон сохранения полной механической энергии. Полная механическая энергия консервативной системы, находящейся в стационарном потенциальном поле, постоянна. Если работа сил стационарного поля над частицей не зависит от пути, пройденного частицей, а зависит только от начального и конечного положения частицы, то такие силы называются консервативными, а поле потенциальным. Закон изменения механической энергии. Приращение механической энергии частицы равно работе неконсервативных сил. Порядок выполнения работы 1. Поставить колебательную систему на металлические пластинки из одного металла так, чтобы она не касалась стенок прорези, а стрелка показывала нуль. 2. Задать начальное отклонение (амплитуду)  = 40 мм. Определить время t для n полных колебаний (n=10), амплитуду  n-го колебания и величину периода по формуле T=t/n. Повторить измерения 5 раз. Начальная амплитуда должна быть одинаковой. Данные измерения занести в табл.1 и вычислить средние значения  и  .3. Измерения повторить для пластинок из двух других металлов и данные также занести в табл.1. 4. Подставляя средние значения и в формулы (9), (11), (12) и (13), определить логарифмический декремент затухания , момент инерции J, коэффициент пропорциональности k и коэффициент трения качения для каждой пары металлов (цилиндр-пластинка). Значения m, l и R даны на установке.5. Сравнить полученные в трех опытах значения момента инерции J, вычислить его среднее значение < J >. Все данные занести в табл.2. Таблица 1. m=… кг, R=… м, l=… м, |AD| =… м, = … м.
Таблица 2.
< J >=............ кгм2 Контрольные вопросы 1. Каков механизм возникновения момента сил трения качения? 2. Каков физический смысл коэффициента трения качения? В чем причина затухания колебаний системы? 3. Чему равен момент сил сопротивления качению, как он направлен? 4. Когда сохраняется и когда изменяется полная механическая энергия системы? 5. Что такое логарифмический декремент затухания? 6. Что такое динамическое уравнение затухающих колебаний? 7. Выведите расчетные формулы для определения момента инерции J (11) и коэффициента К (12). Литература. 1.Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.III, §21, 24, гл.VII, §53, 54 Лабораторная работа №8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||