Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"

• Название: Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
• Дата: 04.04.2022
• Размер: 2.35 Mb.
• Имя файла: mu_1_lab.doc
• Тип: Методические указания; #441829
• страница: 1 из 17

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

"Тульский государственный университет"

Кафедра физики

Руководство к выполнению

лабораторных работ

по дисциплине "Физика"

Часть I.

Механика и молекулярная физика


под ред. Семина В.А.

Тула

Издательство ТулГУ

2011

УДК 53(076.5)
Руководство к выполнению лабораторных работ по дисциплине "Физика". Часть I. Механика и молекулярная физика. / под ред. Семина В.А. Тула: Изд-во ТулГУ, 2011. 104 с.
ISBN 987–5–7679–1851–5

Данный сборник содержит методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика".

В описании каждой лабораторной работы содержатся рекомендации по порядку выполнения, краткие теоретические сведения и контрольные вопросы для подготовки к сдаче лабораторной работы.

Табл.34. Илл. 59. Библиогр.: 3 назв.
Печатается по решению библиотечно-издательского совета Тульского государственного университета
Авторы лаб.6а: Бубенцов В.Г., Лагун И.М.

Рецензент: д-р техн. наук, проф. Чуканов А.Н.

Ó Семин В.А.

Ó Изд-во ТулГУ, 2011
ISBN 987–5–7679–1851–5

Оглавление.

Лаб.1. Исследование косого удара о наклонную плоскость...................................................................................................4

Лаб.2. Упругий удар шаров...............................................10

Лаб.3а. Изучение скорости пули с помощью баллистического маятника...............................................................................15

Лаб.3б. Измерение скорости пули с помощью физического маятника.....................................................................................20

Лаб.3в. Изучение скорости пули с помощью вращающейся платформы.................................................................................26

Лаб.4. Изучение вращательного движения.....................30

Лаб.5. Определение моментов инерции методом колебаний..................................................................................................34

Лаб.6. Определение радиуса кривизны вогнутой поверхности методом катающегося шарика..........................................40

Лаб.6а. Определение момента инерции тел методом крутильных колебаний...................................................................46

Лаб.7. Определение коэффициента трения качения......54

Лаб.8. Определение силы трения скольжения................61

Лаб.9. Определение ускорения свободного падения с помощью физического маятника.....................................................66

Лаб.10. Изучение колебаний пружинного маятника......71

Лаб.13. Определение показателя адиабаты методом Клемана и Дезорма...................................................................................79

Лаб.14. Определение коэффициента поверхностного натяжения воды методом отрыва кольца........................................88

Лаб.15. Определение коэффициента вязкости жидкости по методу Cтокса...........................................................................94

Лаб.16. Определение длины свободного пробега и эффективного диаметра молекул воздуха.........................................100

Лабораторная работа №1

Исследование косого удара о наклонную плоскость

Цель работы: рассмотреть кинематику движения шара после удара о плоскость; определить коэффициент восстановления скорости шара.

Теоретическая часть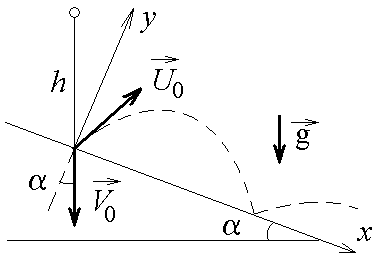




Рис.1
В данной работе рассматривается кинематика движения тела под углом к горизонту в результате соударения с наклонной плоскостью.


Рис. 1
Стальной шарик, падая с некоторой высоты, перед ударом о наклонную плоскость имеет скорость , а отскочив от нее, (см. рис.1). Выберем систему координат, как показано на рис.1, поместив начало координат O в точку первого соударения шарика с наклонной плоскостью. Проекции скоростей и на ось X равны, то есть V_ox = U_ox, так как удар можно считать мгновенным, и действие силы тяжести и силы трения за короткое время не окажет существенного влияния на импульс шарика вдоль оси X (закон сохранения проекции импульса). Рассеяние механической энергии при ударе характеризуется коэффициентом восстановления скорости k_c.

Коэффициентом восстановления скорости тела при ударе о массивную неподвижную поверхность называется отношение , где V_n и U_n – проекции скоростей тела соответственно до и после удара на нормаль к поверхности.

Для данной работы согласно рис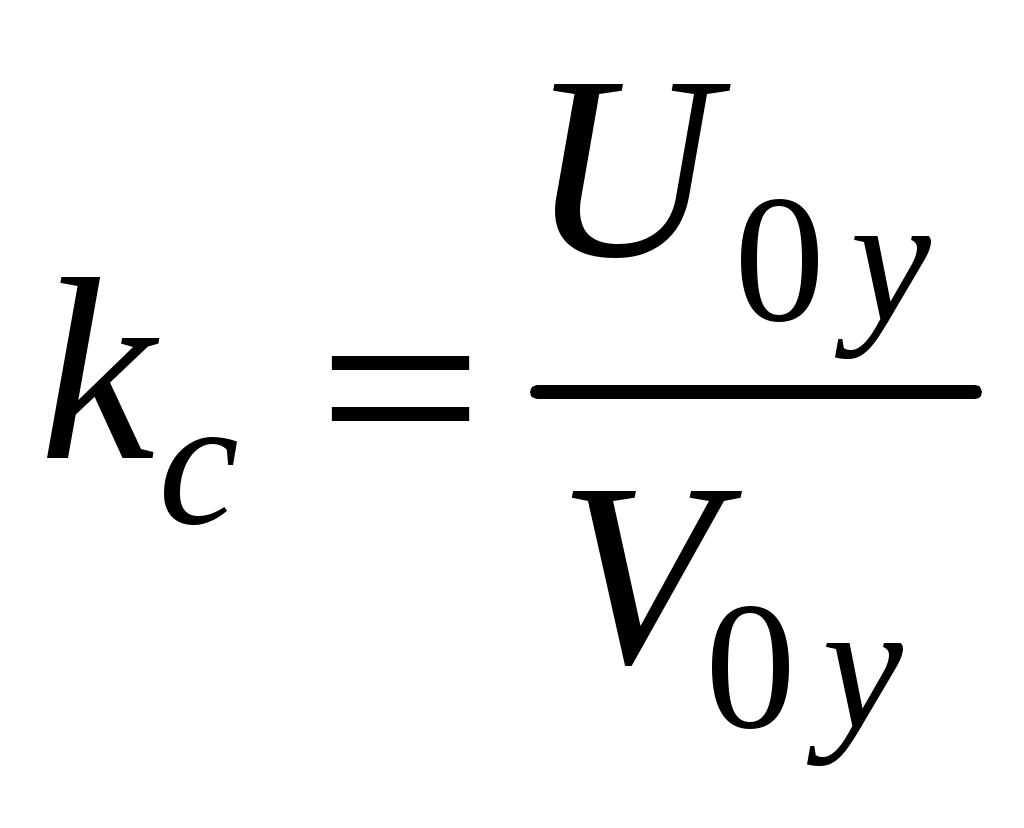.1

(1)

где V_0y и U_0y - проекции на ось y скоростей шарика соответственно до и после первого удара о наклонную плоскость.

Отскочив от наклонной плоскости в точке O со скоростью , шарик будет двигаться в воздухе с постоянным ускорением (сопротивлением воздуха пренебрегаем) и второй раз ударится о наклонную плоскость. Положение шарика при втором соударении относительно точки O определим из закона движения в проекции на ось x

.

При выбранном начале координат и положительном направлении x, как показано на рис.1, , , , поэтому расстояние x между первым и вторым соударением (2)

Время t между двумя соударениями найдем из закона движения в проекции на ось y



Здесь y = 0, , с учетом (1) , . Поэтому



откуда (3)

определим из закона сохранения полной механической энергии (потерями на сопротивление воздуха пренебрегаем)

(4)

где mgh – потенциальная энергия шарика в точке A, из которой он начинает падать без начальной скорости (в точке О потенциальную энергию шарика принимаем равной нулю); – кинетическая энергия шарика в точке О перед ударом о наклонную плоскость.

Из равенства (4) имеем

(5)

Подставив (3) и (5) в (2), найдем



Отсюда 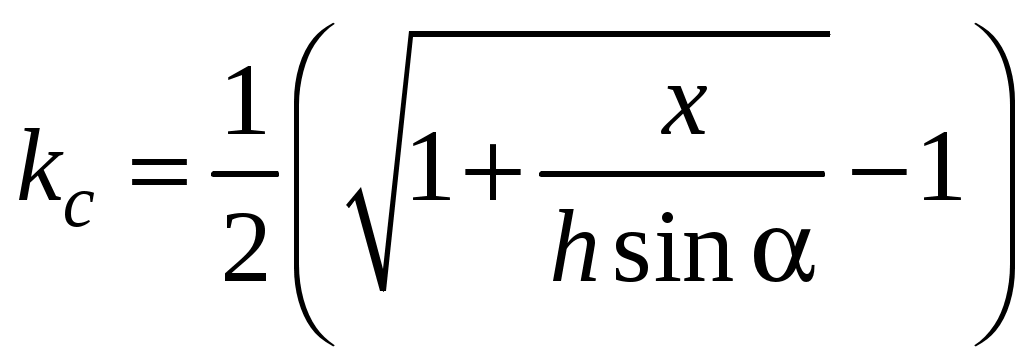. Решив это квадратное уравнение, получим

(6)

В реальных случаях 0 < k_c < 1.
Закон сохранения полной механической энергии

Полная механическая энергия консервативной системы, находящейся в стационарном потенциальном поле, постоянна:



где U_соб – собственная потенциальная энергия системы - это энергия взаимодействия друг с другом всех частиц системы. Она зависит от взаимного расположения частиц системы; U_внеш – внешняя потенциальная энергия системы - это сумма потенциальных энергий всех ее частиц, находящихся во внешнем стационарном потенциальном поле; K – кинетическая энергия системы – это сумма кинетических энергий составляющих ее частиц.

Если работа сил стационарного поля над частицей не зависит от пути, пройденного частицей, а зависит только от начального и конечного положения частицы, то такие силы называются консервативными, а поле потенциальным.

Неупругое соударение тел

Абсолютно упругим называется такое соударение тел, при котором их суммарная полная механическая энергия не меняется.

На практике абсолютно упругого соударения не встречается. За счет работы внутренних диссипативных сил часть полной механической энергии соударяющихся тел превращается в тепловую (внутреннюю) энергию. Полная механическая энергия системы убывает, а соударяющиеся тела деформируются (изменяют свою форму). Такой удар называется неупругим.

Если после соударения тела движутся с одной скоростью вместе, то удар называется абсолютно неупругим. Таким образом, при неупругом соударении полная механическая энергия не сохраняется.

Порядок выполнения работы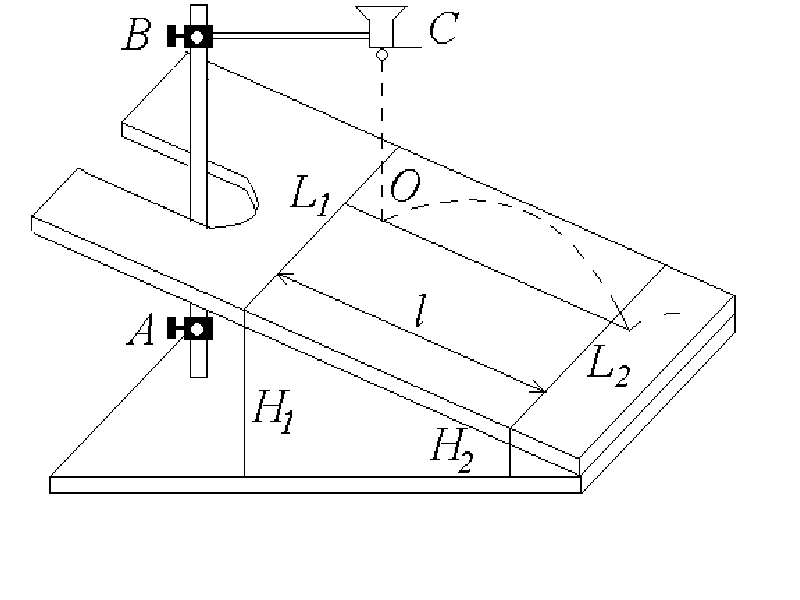


Рис.2

1. Перемещением муфты А (рис.2) установить произвольный наклон плоскости (примерно 10-15°). Измерить высоты H₁ и H₂, длину наклонной плоскости l между линиями L₁ и L₂ (см.рис. 2) и определить .

Примечание. Можно произвольно изменять длину наклонной плоскости , изменяя при этом другие высоты H₁ и H₂.

2. Перемещением муфты B установить произвольную высоту h (17 – 20 cм) бункера C над наклонной плоскостью. Отцентрировать установку бункера так, чтобы шарик после отскока ударился еще один раз о наклонную плоскость в направлении ее продольной оси.

3. Положить на наклонную плоскость узкую полоску бумаги краем вдоль черты L₁, накрыть сверху копировальной бумагой и закрепить оба листа скобой. При проведении эксперимента скобу не трогать.

4. Поместить шарик в бункер C в слегка открытое отверстие (это позволит более точно фиксировать начальное положение шарика). Затем медленно открыть заслонку, дав шарику провалиться. Ударившись о плоскость, шарик отскочит и оставит след на бумаге.

5. Обозначить точку удара на бумаге точкой 1. Отогнуть от линии L₁ и полоску бумаги и копировальную бумагу таким образом, чтобы повторное падение шарика из бункера пришлось на металлическую поверхность; отскочив от нее, шарик второй раз ударится о поверхность и оставит след на бумаге. Эту точку обозначить цифрой 1'.

6. Повторить опыт при отогнутой бумаге 9 раз, обозначая следы от повторных ударов соответственно 1', 2', ..., 3'.

7. Снять листы с плоскости, определить расстояние x_i между точками 1-1', 1-2', 1-3', ..., 1-9' и занести в табл.1.

8. Вычислить среднее значение .

9. Определить случайные отклонения ∆x_i = x_i – < x > каждого измерения расстояния, среднее квадратичное отклонение . Вычислить погрешность ∆x результата измерений: (n-количество точек).

10. Вычислить < k > по формуле (6), подставляя x = < x >. Принимаем радиус шарика r << h.

11. Вычислить абсолютную ∆k_c и относительную E погрешности: ; .

12. Результаты измерений и расчетов записать в табл.1 и 2.
Таблица 1

xi, мм	∆xi, мм	(∆xi) 2, мм2

Таблица 2

l, мм	h, мм	H1,мм	H2,мм	sinα	S, мм	∆x,мм	< kc >	∆kc	E, %

13. Записать результат в виде: .
Контрольные вопросы
1. Что такое коэффициент восстановления скорости, какова методика его определения в данной работе?

2. Записать закон движения шарика между первым и вторым соударениями с наклонной плоскостью координатным способом. Как определить расстояние x и время t между этими соударениями?

3. Сформулировать закон сохранения полной механической энергии. Как он применяется в данной работе?
Литература

1. Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.III, §19, 24, 25, 27

Лабораторная работа №2