Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Изучение скорости пули с помощью баллистического маятникаЦель работы: Использование на практике законов сохранения импульса и механической энергии для измерения скорости пули. Теоретическое описание Скорость поступательного движения пули определяем с помощью баллистического маятника. Он представляет собой открытый с одного конца пустотелый массивный цилиндр, подвешенный на двойном бифилярном подвесе. Внутренняя часть цилиндра заполнена пластилином, чтобы соударение летящего тела (пули), скорость которого нужно измерить, с баллистическим маятником носило неупругий характер. После неупругого соударения тела движутся как единое целое с общей скоростью. Пуля массой m1, движущаяся в горизонтальном направлении со скоростью  влетает в цилиндр баллистического маятника и застревает в нем. После соударения цилиндр маятника массой m2 совместно с застрявшей в нем пулей приобретает некоторую скорость  . На основании закона сохранения импульса можем записать в векторном виде и в проекции на ось, совпадающую с направлением движения пули и маятника с пулей,  (1)Непосредственно после удара система "маятник-застрявшая пуля" обладает кинетической энергией  , к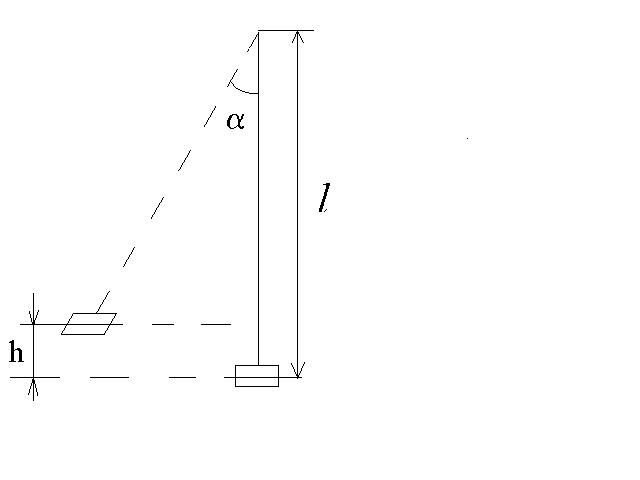оторая по мере отклонения маятника от вертикального положения превращается в потенциальную энергию  . Если пренебречь потерями энергии на трение, то на основании закона сохранения механической энергии получим (2)г  де h – высота подъема центра масс системы "маятник-пуля". Из рисунка следует, что  ,где – угол отклонения маятника от вертикального положения; l – длина подвеса. Отсюда  ,Подставляя значение h в (2), получаем 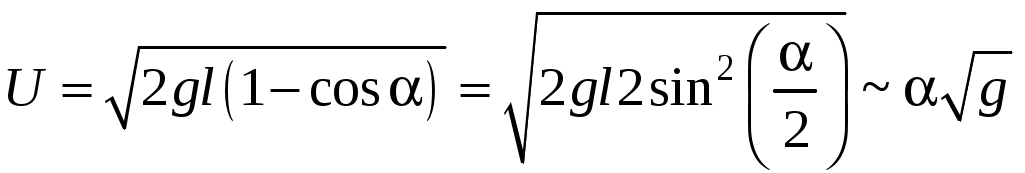 (3)(при малых углах  , где  измеряется в радианах).Подставляя (3) в (1), получаем искомую скорость  (4)Закон сохранения полной механической энергии Полная механическая энергия консервативной системы, находящейся в стационарном потенциальном поле, постоянна:  где Uсоб – собственная потенциальная энергия системы – это энергия взаимодействия друг с другом всех частиц системы. Она зависит от взаимного расположения частиц системы; Uвнеш – внешняя потенциальная энергия системы – сумма потенциальных энергий всех ее частиц, находящихся во внешнем стационарном потенциальном поле; K – кинетическая энергия системы – это сумма кинетических энергий составляющих ее частиц. Если работа сил стационарного поля над частицей не зависит от пути, пройденного частицей, а зависит только от начального и конечного положения частицы, то такие силы называются консервативными, а поле потенциальным. Закон сохранения импульса Замкнутой системой называется система, на которую не действуют никакие внешние тела (или их взаимодействием можно пренебречь). Импульс системы частиц остается постоянным, т.е. не меняется со временем, если система замкнута или сумма всех внешних сил, действующих на частицы этой системы, равна нулю:  У незамкнутой системы может сохраняться не импульс  , а его проекция px на направление x, если результирующая проекций всех внешних сил на это направление равна нулю.Порядок выполнения работы 1. В табл.1 записать значение массы пули m1, массы маятника m2, длины нити l и их погрешности (m1 и m2 в граммах указаны на пуле и цилиндре). Таблица 1.
2. Вставить пулю в ствол пружинного пистолета. 3. Нажимая на спуск, произвести выстрел и отсчитать по шкале угол отклонения маятника от вертикального положения. 4. Значение угла отклонения записать в табл.2. Таблица 2
 = ... o, = ... рад.5. Измерения провести не менее 9 раз; определить среднее значение угла отклонения , случайные отклонения каждого измерения  , среднее квадратичное отклонение ,гдеn – число измерений (n=9); погрешность результата измерений  .6. По формуле (4) определить среднее значение скорости пули, подставляя среднее значение , выраженное в радианах.7. Относительную и абсолютную погрешности результата рассчитать по формулам 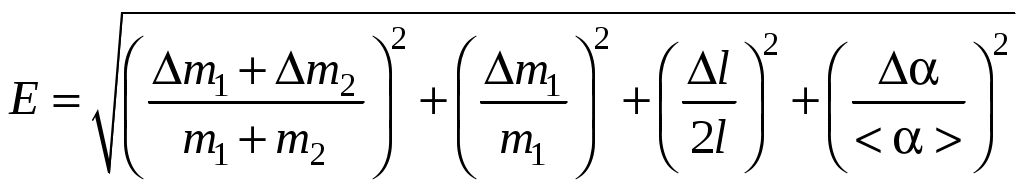 ,  и записать в табл.3. Таблица 3
Контрольные вопросы 1. Когда импульс системы сохраняется? 2. Будет ли система "пуля-маятник" замкнутой? 3. Сохраняется ли импульс системы "пуля-маятник" при движении ее после удара? Почему? 4. Вид удара в данной работе. 5. Когда полная механическая энергия системы сохраняется? Равны ли кинетические энергии системы "пуля-маятник" до и после удара? 6. Получить расчетную формулу скорости пули. Литература 1.Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.III, §24, с.27-29, 226-228; Лабораторная работа №3,б |
, м/с
, м/с