Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Изучение скорости пули с помощью вращающейся платформы.Цель работы: Определение скорости пули при выстреле с помощью закона сохранения проекции момента импульса. Теоретическое описание 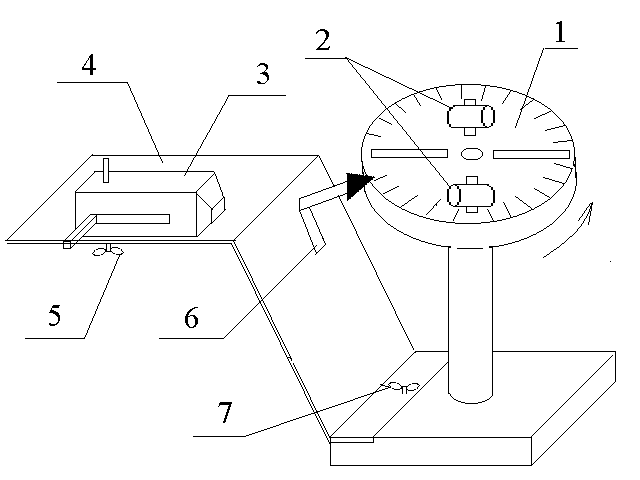 Рис.1 Схема установки. Установка представляет из себя диск 1 (платформу), закрепленный на оси (рис.1).На диске имеются продольные прорези, вдоль которых могут перемещаться ловушки 2 и закрепляться на нужном расстоянии от оси вращения. Пистолет 3 закреплен сбоку на подставке 4, может поворачиваться и перемещаться для стрельбы в ловушку (по касательной) и закрепляется винтом-барашком 5. Подставка также может поворачиваться, перемещаться и закрепляется винтом-барашком 7. Угол поворота диска определяется с помощью делений на нем и указателя 6 на подставке. Производя выстрел из пружинного пистолета в ловушку, установленную на вращающейся платформе (диске),приведем во вращательное движение платформу. На основании закона сохранения проекции момента импульса можно записать:  , (1)где m – масса пули, l – плечо импульса пули, т.е. расстояние от оси вращения до линии импульса пули, V – скорость пули, J – момент инерции платформы с ловушкой относительно оси вращения, – угловая скорость платформы сразу после удара. Отсюда следует  (2)Учтя, что после удара платформа вращается равнозамедленно и поворачивается до полной остановки на угол , выразим через угловое ускорение и угол :  . Величину , в свою очередь, можно найти из дополнительного наблюдения вращательного движения диска, вызванного толчком руки: , (3)где – угол поворота платформы до остановки,t – время этого поворота. Окончательно для V имеем  . (4)Закон сохранения полной механической энергии Полная механическая энергия консервативной системы, находящейся в стационарном потенциальном поле, постоянна:  где Uсоб – собственная потенциальная энергия системы – это энергия взаимодействия друг с другом всех частиц системы. Она зависит от взаимного расположения частиц системы; Uвнеш – внешняя потенциальная энергия системы – сумма потенциальных энергий всех ее частиц, находящихся во внешнем стационарном потенциальном поле; K – кинетическая энергия системы – это сумма кинетических энергий составляющих ее частиц. Если работа сил стационарного поля над частицей не зависит от пути, пройденного частицей, а зависит только от начального и конечного положения частицы, то такие силы называются консервативными, а поле потенциальным. Закон сохранения момента импульса Замкнутой системой называется система, на которую не действуют никакие внешние моменты сил (или их действием можно пренебречь). момент импульса системы остается постоянным, т.е. не меняется со временем, если система замкнута или суммарный момент всех внешних сил, действующих на частицы системы, равен нулю. Таким образом в инерциальной системе отсчета момент импульса замкнутой системы частиц  У незамкнутой системы может сохраняться не сам момент импульса  , а его проекция на некоторую неподвижную ось z, если проекция суммарного момента  всех внешних сил на эту ось z равна нулю.Порядок выполнения работы 1. Массы диска, ловушки, пули указаны в описании или на самих телах. 2. Установить ловушки симметрично на произвольном расстоянии от оси вращения диска, закрепить их (отверстием в сторону пистолета). 3. Толкнуть диск рукой и пустить секундомер. Зафиксировать угол и время поворота t диска. Опыт проделать 9 раз, определить i и ti. Найти средние значения <> и
4. Зарядить пистолет, повернуть его так, чтобы при выстреле пуля попала в ловушку в направлении по касательной к траектории движения ловушки. 5. Произвести выстрел. Определить угол поворота диска. Опыт повторить 9 раз, определяя каждый раз i, затем определить  .6. Определить момент инерции диска с ловушками по формуле  ,где m∂ – масса диска, r∂ – радиус диска, mл – масса ловушки, l – расстояние до центра вращения.
7. Определить угловое ускорение по формуле (3), подставляя = <>, скорость пули по формуле (4), подставляя = <>.
Контрольные вопросы 1. Когда момент импульса системы сохраняется? 2. Записать в векторной форме до и после удара момент импульса системы в данной работе, определить его модуль и направление. 3. Сохраняется ли момент импульса системы в данной работе при вращении ее после удара? Почему? 4. Вид удара в данной работе. 5. Когда полная механическая энергия системы сохраняется? Может ли в некоторой системе не сохраняться механическая энергия и оставаться постоянным момент импульса? 6. Получить расчетную формулу скорости пули. 1.Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.III, §24, с.27-29; Лабораторная работа №4 |