Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Упругий удар шаровЦель работы: ознакомиться с явлением удара на примере соударения шаров, рассчитать коэффициент восстановления энергии, проверить закон сохранения импульса. Теоретическое описание. О 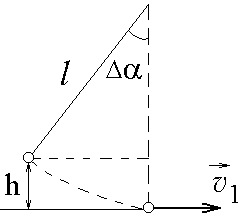 Рис.1 тклоним шарик А с массой  на угол  , где  и  показания по шкале измерения. При этом шарик поднимется на высоту  (см. рис.1). Как видно из рисунка высоту подъема можно выразить через длину подвеса и угол отклонения : (1)После освобождения шарика без начальной скорости он будет ускоряться и в нижней точке своей траектории приобретет горизонтальную скорость 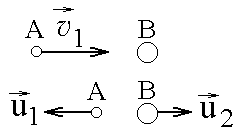 , которую можно найти из закона сохранения энергии:  , откуда следует (2) Рис.2 В нижней точке своей траектории шарик А сталкивается с шариком В, и после очень короткого удара они разлетаются в противоположные стороны с горизонтальными скоростями  и  (см. рис.2). Так как во время удара силы натяжения нитей и силы тяжести, действующие на шарики, направлены по вертикали, то должен выполняться закон сохранения горизонтальной проекции импульса системы:  (3)В большинстве случаев реальные удары тел не являются упругими из-за возникновения диссипативных сил внутри этих тел (внутреннее трение), поэтому кинетическая энергия системы в целом при ударе уменьшается. Коэффициентом восстановления кинетической энергии называется величина, равная:  (4)Коэффициент восстановления энергии всегда меньше единицы: 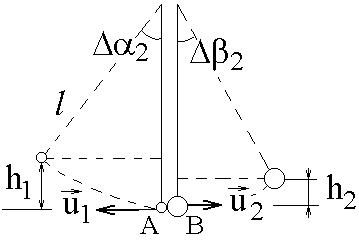 . Равенство единице означает полное сохранение энергии, что может быть только в идеальном случае отсутствия диссипативных сил в системе. Рис.3 После столкновения (см. рис.3) действие диссипативных сил внутреннего трения прекращается, и, если пренебречь потерей энергии во время движения из-за сопротивления воздуха, можно воспользоваться законом сохранения энергии для каждого шара в отдельности. Шар А отклонится на угол  и поднимется на высоту  , а шар В отклонится на угол  и поднимется на высоту  Используя уравнения 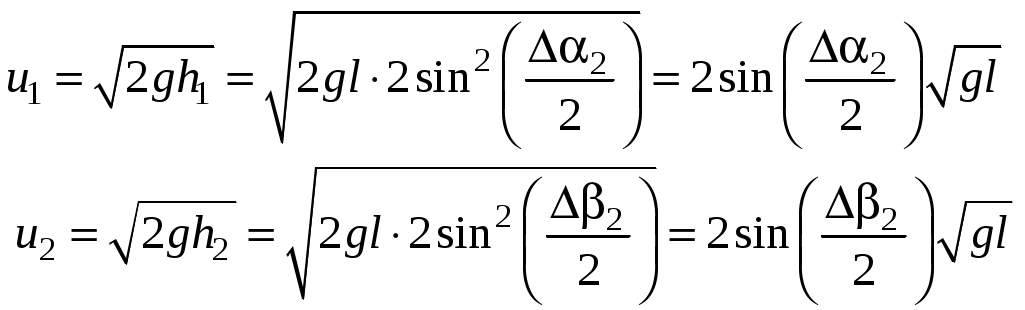 и  аналогичные уравнениям (1) и (2), выразим скорости шаров после удара: (5)Подставляя (2) и (5) в (4), получим выражение для расчета коэффициента восстановления энергии: 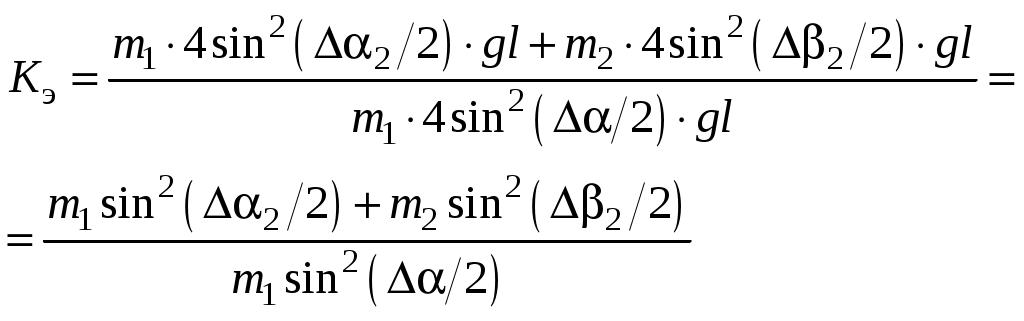 (6)Подставляя (2) и (5) в (3), получим закон сохранения импульса в виде:  (7)Порядок выполнения работы З 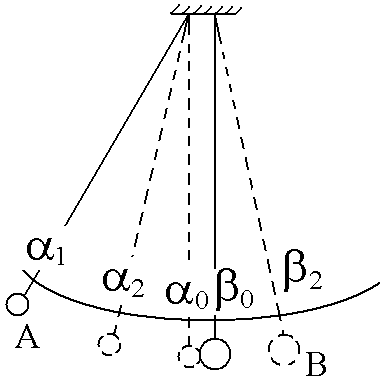 Рис.5аписать начальные положения 0 и 0, соответствующие точкам пересечения нитей бифилярных подвесов с линией деления шкалы, когда шары неподвижны. Здесь и в дальнейшем обозначение "" относится к шару А с меньшей массой m1, а "" – к шару В с меньшей массой m2. Отклонить шар А на угол 1 от 10º до 15 и отпустить без начальной скорости. Произвести отсчет первого отброса обоих шаров 2 и 2 (так как сразу практически невозможно взять два отсчета, то поступают так: сначала берут отсчет для одного шара, затем производят повторный удар из того же положения шара А и берут отсчет для второго шара). Удар из данного положения производят не менее 10 раз, чтобы для каждого шара получить не менее пяти значений отбросов нитей после удара (2 и 2). Найти среднее <2> и <2>. Опыт проделать для двух других значений 1. (от 20 до 25, от 30 до 35). Заполнить таблицу 1. Проверить закон сохранения импульса (7). Для этого рассчитать скорости  и  по формулам (2) и (5), учитывая, что ,  ,  . Расcчитать левую часть уравнения (7)  и правую часть уравнения (7)  и занести в таблицу 2. Рассчитать на сколько процентов отличаются левая и правая часть уравнения (7) по формуле:  Вычислить коэффициент восстановления энергии по формуле (6). Таблица 1.
, = …  , = … Таблица 2.
Контрольные вопросы Будет ли система шаров замкнутой? Сформулировать закон сохранения импульса системы. Сохраняется ли импульс системы шаров после удара? Почему? Вид удара в данной работе. Проанализируйте полученный коэффициент восстановления энергии. Когда полная механическая энергия системы сохраняется? Равны ли кинетические энергии системы шаров до и после удара? Может ли в некоторой системе не сохраняться механическая энергия и оставаться постоянным момент импульса? Получить расчетные формулы скоростей шаров после удара. Литература Савельев И.В. Курс общей физики. т.1. М: Наука , 1970.- гл. II, §23, с.75-77, гл. III, §27-30, с.89-106 Лабораторная работа №3, А | ||||||||||||||||||||||||||||||||||||||
