Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
Определение момента инерции тел методом крутильных колебанийЦель работы – изучить метод крутильных колебаний для рассчета момента инерции тел разной формы. Сравнить экспериментальные значения моментов инерции этих тел с теоретическими расчетами. Описание лабораторной установки. 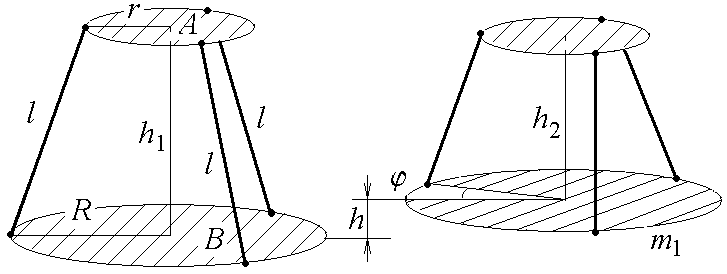 Рис.1. Схема установки Моменты инерции различных тел могут быть измерены методом крутильных колебаний с помощью так называемого трифилярного подвеса. Трифилярный подвес состоит из диска В массой Порядок выполнения работы 1. Измерить линейкой радиусы дисков R и r, а также длину нитиl. Занести данные в Таблицу 1. 2. Резко повернуть рукой диск 3. С помощью секундомера определить время Таблица 1.
4. Положить на нижний диск исследуемое тело так, чтобы центры масс тела и диска были на одной оси. Масса 5. Определить время 6. Используя экспериментальные данные, вычислить момент инерции Iэксп исследуемого тела по формуле 7. Измерить размеры исследуемого тела и из таблицы 3 для данной формы тела вычислить теоретический момент инерции Iтеор тела относительно той же оси, что и при эксперименте. 8. Сравнить теоретическое Iтеор и экспериментальное Iэксп значения момента инерции. Для этого вычислить относительное отклонение 9. С пункта 3 по 8 проделать аналогично измерения и вычисления с другими телами . Таблица 2.
Таблица 3. Моменты инерции плоских тел относительно оси, проходящей через центр масс перпендикулярно их плоскости. 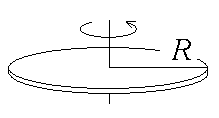 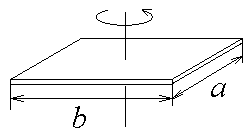 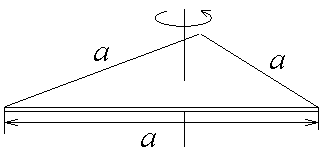 Диск Прямоугольник Равностор. треугольник Краткие теоретические сведения При условии малых колебаний, т.е. Пусть диск поднялся на максимальную высоту Тогда приращение потенциальной энергии равно: При последующем вращении диска потенциальная энергия переходит в кинетическую энергию вращательного движения где В момент прохождения положения равновесия кинетическая энергия принимает максимальное значение, и, пренебрегая трением, можно записать закон сохранения энергии: Угловую скорость диска можно найти, взяв производную от из (1): тогда Величину hможно найти, считая, что при повороте диска на малый угол где учтено, что (см. рис.1) В результате подстановки (4) и (3) в (2), получим расчётную формулу для момента инерции маятника массой По зависимости (5) можно рассчитать момент инерции как нагруженного исследуемой пластиной, так и ненагруженного диска В. Тогда, вследствие аддитивности, момент инерции исследуемого тела (пластины) легко определяется по формуле: где Момент инерции есть мера инертности тела при его вращательном движении. Это значит, что чем больше момент инерции, тем больший момент сил необходимо приложить к телу, чтобы заставить тело вращаться, если оно покоилось, или остановить, если вращалось. Момент инерции материальной точки: Момент инерции зависит от формы и размеров тела или системы, а также от положения и ориентации в пространстве оси, относительно которой определяется момент инерции. Например, если известен момент инерции тела относительно оси, проходящей через его центр масс, то относительно любой другой оси его можно рассчитать с помощью теоремы Штейнера: момент инерции тела относительно произвольной оси О IО = IС + md2. Моменты инерции тел относительно оси, проходящей через центр масс IС можно определить, пользуясь определением (*) и разбивая тело на элементы 1. Момент инерции плоской прямоугольной пластины относительно оси, проходящей через центр масс перпендикулярно ее плоскости. М 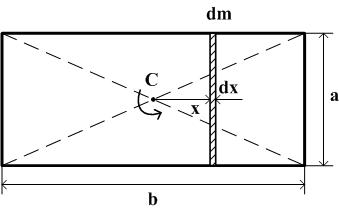 омент инерции выделенного элемента (в виде стержня массой dm, длиной aи толщиной dxкак показано на рисунке) по теореме Штейнера: омент инерции выделенного элемента (в виде стержня массой dm, длиной aи толщиной dxкак показано на рисунке) по теореме Штейнера: Из геометрических соображений Тогда момент инерции пластины: 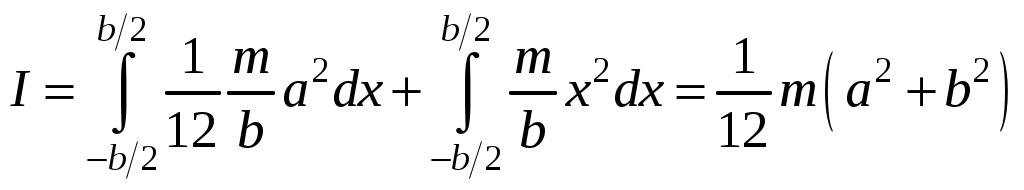 2. Момент инерции плоской треугольной пластины относительно оси, проходящей через центр масс перпендикулярно ее плоскости. Р 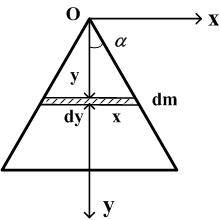 азобьем пластину на тонкие стержни массой dm длиной 2x и высотой dy, как показано на рисунке. Так как для стержня длины азобьем пластину на тонкие стержни массой dm длиной 2x и высотой dy, как показано на рисунке. Так как для стержня длины где массу стержня где Тогда масса стержня: 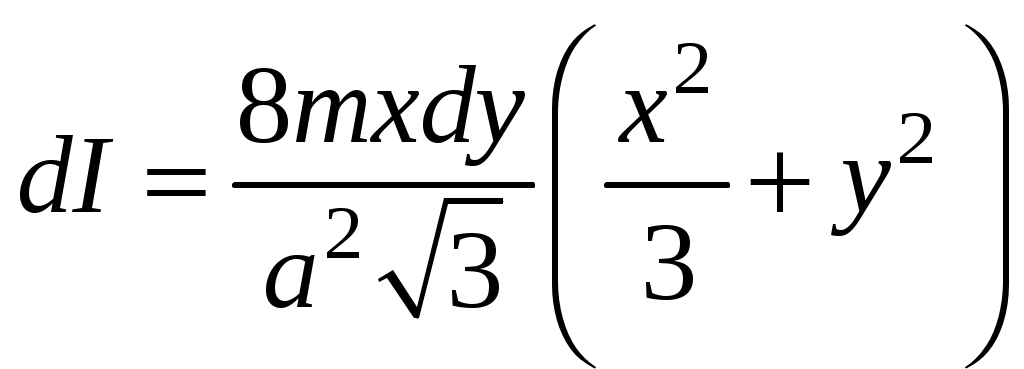 С учетом того, что для равностороннего треугольника Т 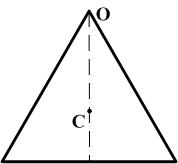 огда огда 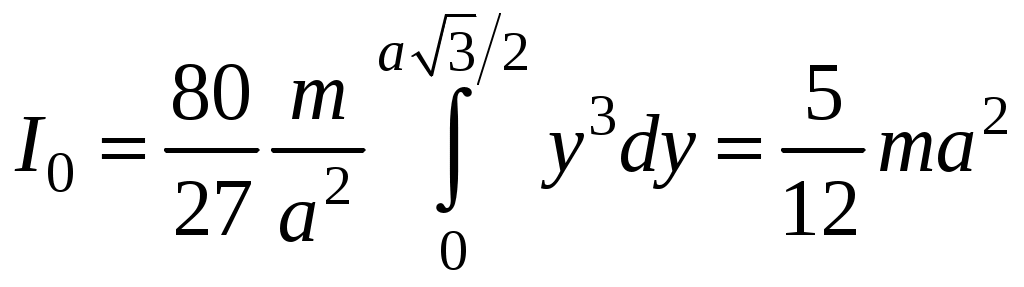 . Но по теореме Штейнера . Но по теореме Штейнера Контрольные вопросы 1. В чем заключается физический смысл момента инерции? 2. От чего зависит момент инерции? 3. Сформулируйте теорему Штейнера. 4. С помощью теоремы Штейнера объясните, относительно какой оси момент инерции тела минимален (максимален)? 5. Получите расчетную формулу для момента инерции плоской прямоугольной пластины относительно оси, проходящей через центр масс, и лежащей в плоскости пластины. 6. Получите расчетную формулу для момента инерции пластины в форме равностороннего треугольника относительно оси, лежащей в плоскости пластины и проходящей через одну из его сторон. 7. Как нужно проводить эксперимент в данной работе, чтобы расчетные формулы, которыми вы пользовались, были справедливы Лабораторная работа №7 |
