Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Измерение скорости пули с помощью физического маятникаЦель работы: практическое использование законов сохранения момента импульса и механической энергии для определения скорости пули. Теоретическое описание. В 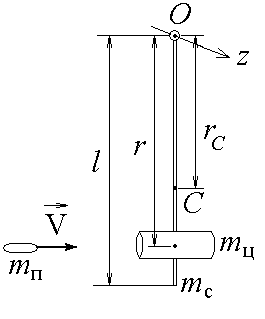 Рис.1 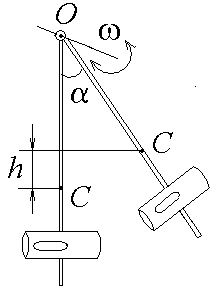 Рис.2 данной работе физический маятник представляет собой цилиндр массой mц (частично наполненный пластилином), укрепленный на тонком стержне массой mc и длиной l (рис.1). Стержень шарнирно закреплен на горизонтальной оси и может вращаться в вертикальной плоскости вокруг точки О. Положение центра масс цилиндра относительно точки О зададим радиусом-вектором  . В маятник стреляют в горизонтальном направлении пулей, имеющей массу mп и скорость  . Пуля входит в пластилин (неупругий удар) и сообщает физическому маятнику угловую скорость  . В результате этого маятник отклонится на угол и его центр масс С поднимется на высоту h (рис.2). Система "пуля-маятник" незамкнутая. Но если считать удар мгновенным, то за время удара маятник не успеет существенно отклониться, и поэтому момент всех внешних сил относительно оси z в течение этого времени будет равен нулю (  внеш = 0).Отсюда вывод: проекция момента импульса  данной системы будет оставаться постоянной относительно оси z ( = const). Момент импульса  относительно точки О (рис.1) для всей системы перед ударом равен моменту импульса пули: ,где  – импульс пули до удара (маятник находится в покое).Направление вектора определяется правилом правого винта (см. приложение), а его модуль (и проекция на ось Z) .Так как ось вращения маятника перпендикулярна плоскости его вращения, то момент импульса  всей системы относительно той же точки О после удара (когда пуля застрянет в пластилине) .Направление вектора совпадает с направлением вектора , а модуль (и проекция на ось Z) .Поскольку система будет вращаться вокруг неподвижной оси Z (см. рис.1), то J – момент инерции всей системы "пуля-маятник" относительно этой оси. На основании закона сохранения проекции момента импульса на ось z имеем  (1)Момент инерции Jвсей системы как величина аддитивная равен сумме моментов инерции составляющих ее тел относительно оси z, т.е.  ,где Jпод – момент инерции подшипника (величина его мала по сравнению с Jc, Jц и Jп и ею можно пренебречь);  – момент инерции стержня; – момент инерции цилиндра (т.к. радиус цилиндра мал по сравнению с r, то момент инерции его рассчитывается, как для материальной точки); – момент инерции пули.Следовательно, в данной работе  , (2)Из равенства (1) скорость пули перед ударом в маятник  . (3)Угловая скорость всей системы после удара может быть определена по закону сохранения механической энергии, который в данном случае запишется в виде  , (4)где  – кинетическая энергия вращательного движения системы после удара пули; – потенциальная энергия системы после отклонения ее на максимальный угол .Здесь  , (5)где m – масса всей системы "пуля-маятник"; mпод – масса подшипника. Из рис.2 следует, что высота подъема центра масс С системы  , (6)Выразив из (4) с учетом (6) и подставив в (3), найдем скорость V пули:  . (7)Центр масс (центр инерции) системы относительно точки О определим по формуле  , (8)где  – радиус-вектор центра масс отдельной детали системы;mi – масса этой детали. Из (8) и рис.1 видно, что 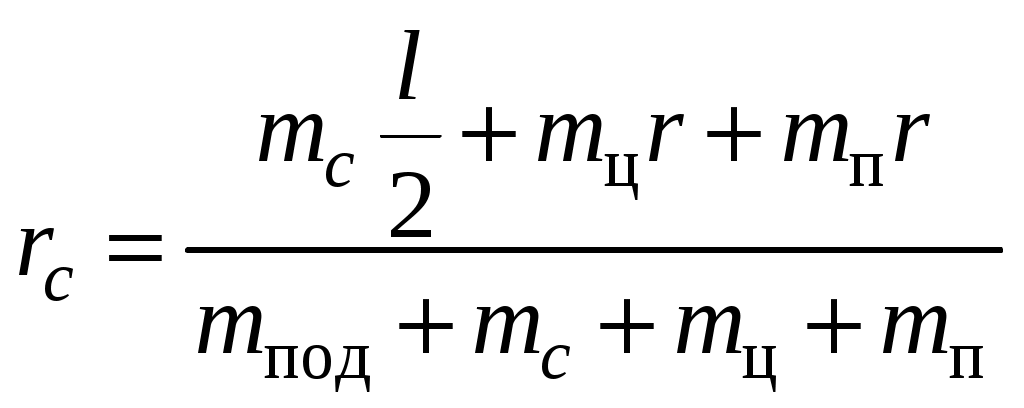 . (9)Приложение Правило правого винта. 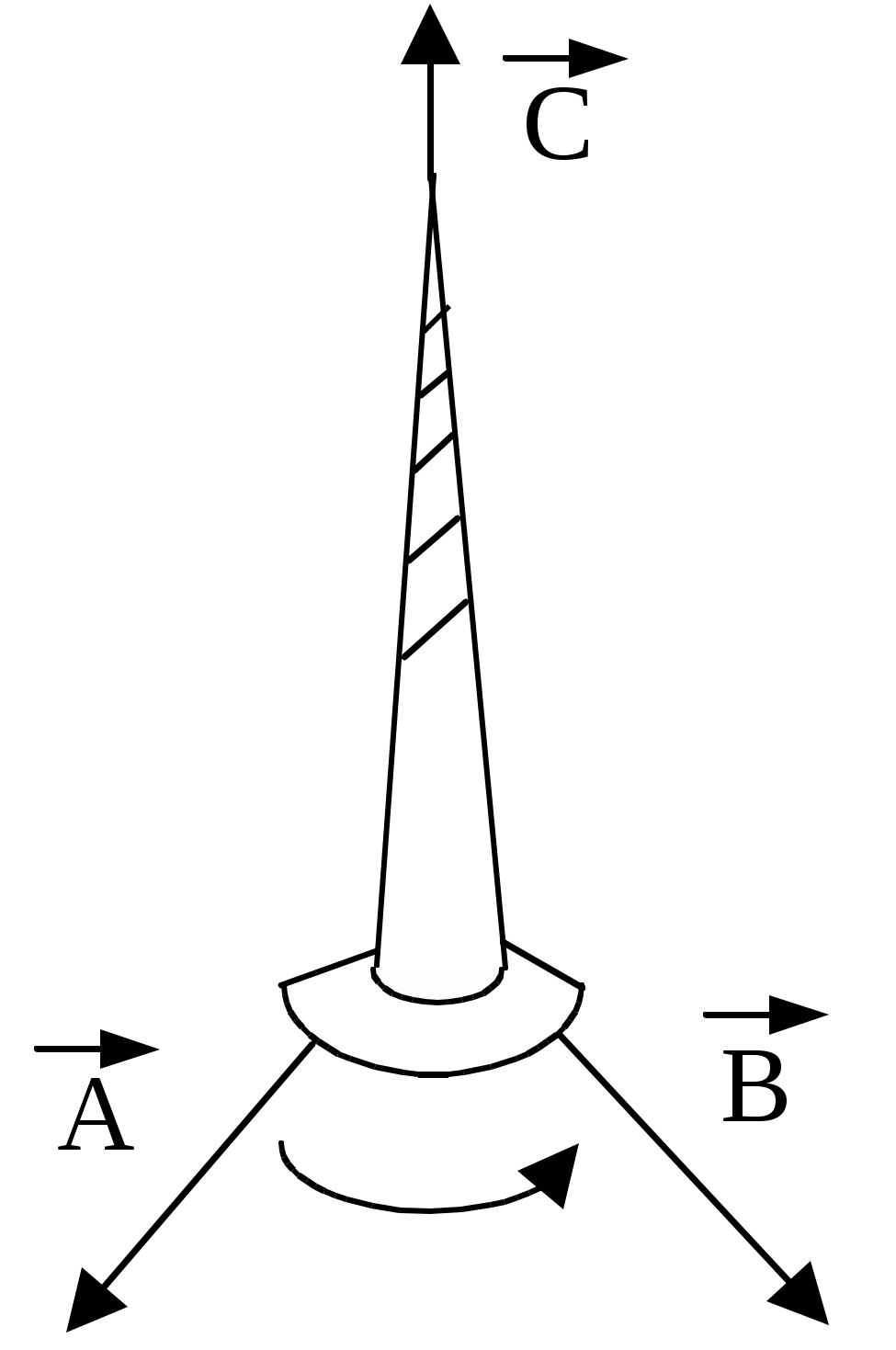 Чаще всего правило правого винта связано с определением направления векторного произведения двух векторов.Векторное произведение, обозначаемое  , двух векторов  и  есть вектор  , модуль которого  , где – угол минимальный угол между векторами и .Направление вектора перпендикулярно плоскости, в которой лежат векторы и , и совпадает с направлением поступательного движения правого винта при его повороте от к на угол, меньший (см. рис.)Порядок выполнения работы З 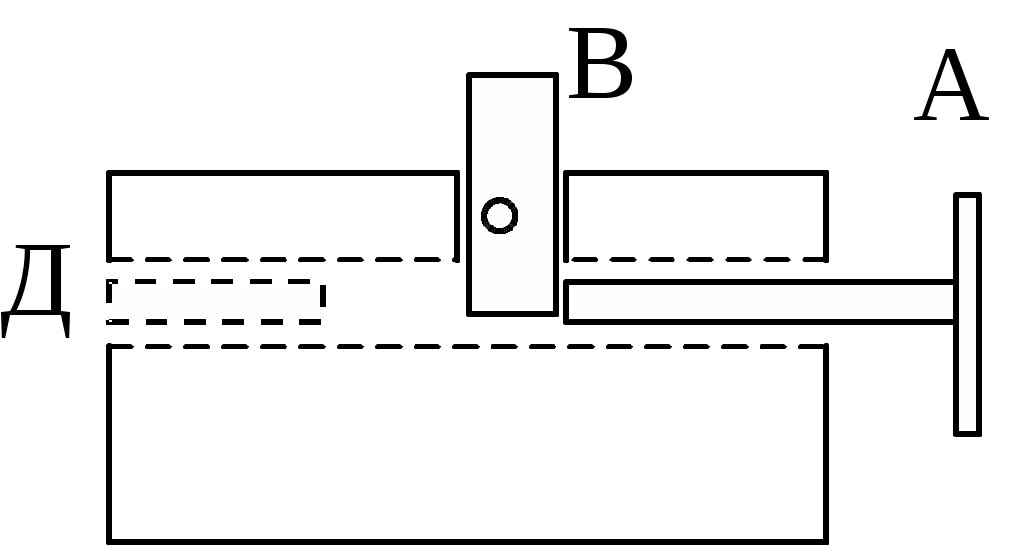 Рис.3арядить пружинную пушку. Для этого оттянуть назад ударный стержень, взявшись за выступ А (рис.3). Стержень оттягивать до тех пор, пока другой рукой не удастся поставить выступ В в вертикальное положение, в котором он удерживает стержень и пружину в сжатом состоянии. Затем в дуло Д пушки заложить пулю (левый край пули совместить с торцом Д). З 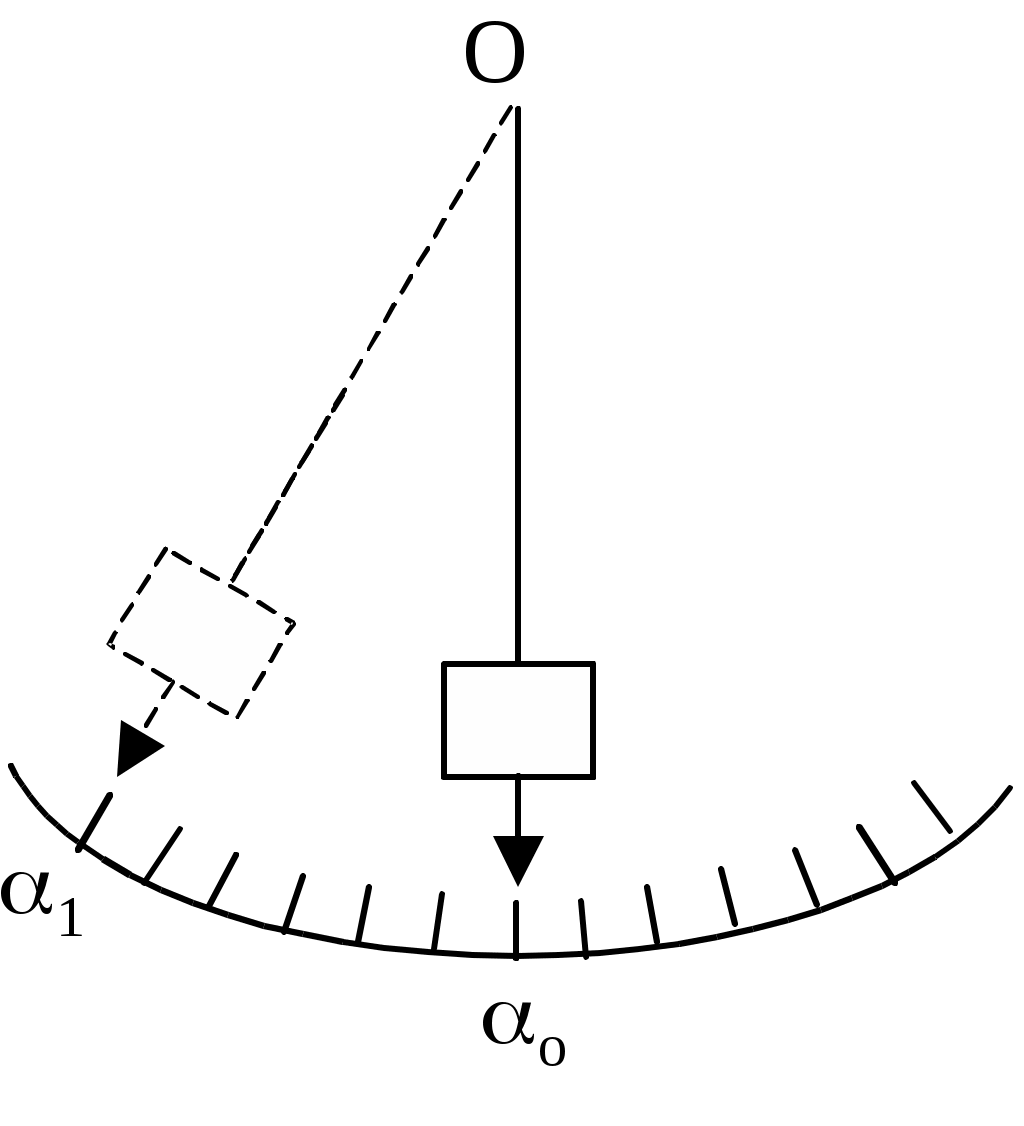 Рис.4аписать начальное положение о острия стержня при неподвижном цилиндре. Цена наименьшего деления шкалы 10' (угловых минут). Повернуть выступ В на себя (приведя в горизонтальное положение), отсчитать положение острия 1 при максимальном отбросе маятника (рис.4) Вычислить угол отклонения маятника = 1 – о. Опыт повторить 5 раз (выстрел производить только по неподвижному маятнику). Найти средний угол отклонения <>. Вычислить массу всей системы "пуля-маятник" m по формуле (5). Масса пули указана на ней, а остальные массы – на установке. Подсчитать момент инерции J всей системы по формуле (2). Определить положение центра масс С системы "пуля-маятник" относительно точки О по формуле (9). Среднюю скорость <V> пули перед ударом в маятник рассчитать по формуле (7), подставляя = <>. Данные измерений и вычислений занести в таблицы 1 и 2. Таблица 1.
о = …o Таблица 2.
Контрольные вопросы 1. Будет ли система "пуля-маятник" замкнутой? 2. Когда момент импульса системы сохраняется? 3. Сохраняется ли момент импульса системы "пуля-маятник" при вращении ее после удара? Почему? 4. Вид удара в данной работе. 5. Когда полная механическая энергия системы сохраняется? Равны ли кинетические энергии системы "пуля-маятник" до и после удара? 6. Может ли в некоторой системе не сохраняться механическая энергия и оставаться постоянным момент импульса? 7. Получить расчетную формулу скорости пули. Литература 1. Савельев И.В. Курс общей физики. т.1. М: Наука , 1986.- гл. III, §24, с.27-29, 2. Иродов И.Е. Основные законы механики: Учеб. пособие. 3-е изд., перераб. и доп. – М.: Высшая школа, 1985. гл.3, §3.4, гл.4, §4.5, гл.5, §5.1, 5.2. Лабораторная работа №3,в |