Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Изучение колебаний пружинного маятникаЦель работы: изучить собственные колебания пружинного маятника (незатухающие в воздухе и затухающие в жидкости), определить характеристики затухающих колебаний. Порядок выполнения работы 1. Определить по шкале «естественную» длину  пружины, укрепленной справа на установке.2. При трех различных грузах в положении равновесия определить длину пружины  .3. В каждом опыте вычислить коэффициент упругости пружины в соответствии с формулой (2) и найти его среднее значение  . Массы всех грузов указаны на них. Данные занести в табл.1.Таблица 1.
4. Подвесить груз к этой же пружине и вывести маятник из положения равновесия, сместив вниз на 2-3 мм, и отпустить. Секундомером измерить время  полных  колебаний (начинать отсчет при прохождении грузом верхнего или нижнего положения). Тогда период колебаний  . Опыт повторить 3 раза с этим грузом и найти среднее значение периода  .5. То же проделать еще с двумя грузами различной массы. Данные занести в табл.2.  Таблица 2.
6. Постройте график зависимости  от массы грузов  . Используя этот график и формулу (3), определить значение коэффициента упругости  : сравнить его со значением, полученным по формуле (2).7. Опыт проделать с пружинным маятником, груз которого помещен в сосуд с водой. Вывести груз из положения равновесия, например на  =20 мм, и, отпустив его, включить одновременно секундомер. Определить время, за которое он совершит  полных колебаний, а также амплитуду колебаний после  колебаний  . Опыт выполнить 3 раза и найти среднее значение периода  и амплитуды -го колебания .Таблица 3.
8. Вычислить логарифмический декремент затухания  ; коэффициент затухания  и коэффициент сопротивления  . Данные измерений и вычислений занести в табл.3.Описание установки 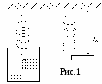 В данной работе маятник представляет собой пружину малой массы с грузом массы на ее конце (см.рис.1). Выведенный из положения равновесия и предоставленный самому себе груз маятника будет совершать собственные колебания. Сопротивление воздуха сравнительно невелико и его можно не учитывать. Тогда период колебаний груза определяется формулой: (1)где - коэффициент упругости пружины.Коэффициент упругости пружины можно найти статическим методом. Если - длина пружины в ненагруженном состоянии, а - длина пружины с грузом в состоянии равновесия, то в этом случае модуль силы тяжести  равен модулю силы упругости  ; , откуда  (2)Коэффициент численно равен силе, которую нужно приложить к пружине при упругой деформации, чтобы растянуть (или сжать) пружину на единицу длины.Из формулы (1) имеем  (3)Выражение (3) позволяет определить значение динамическим способом и предоставляет возможность сравнить его со значением, полученным статическим методом по формуле (2).На пружине, расположенной слева на рис.1, изучаются затухающие колебания груза в жидкости. Опытным путем определяются период колебаний, начальная и через  колебаний амплитуды и подсчитывается логарифмический декремент затухания , коэффициент затухания и коэффициент сопротивления  Теоретическое описание Гармонические колебания.  Гармонические колебания представляют собой периодический процесс, в котором изменение величины происходит по закону косинуса (или синуса). Например, проекция радиуса-вектора  точки, движущейся по окружности, на ось  , лежащую в плоскости движения точки (рис.2), изменяется со временем по косинусоидальному закону. Если окружность имеет радиус  , а угловая скорость вращения точки  постоянна, то проекция Период изменения , очевидно, будет равен  , где  – время одного оборота точки, через которое весь процесс в точности повторяется; – циклическая (круговая) частота;  – начальный угол поворота относительно оси . Следовательно, отличается множителем 2 от частоты : Так как максимальное значение косинуса равно единице, то максимальное значение равно  . Это максимальное значение называется амплитудой колебаний.Аргумент косинуса  носит название фазы колебаний, а - начальной фазы колебаний.Пусть теперь гармонические колебания вдоль оси совершает материальная точка массой . Выясним, какая при этих условиях на нее должна действовать сила.Проекция скорости точки на ось  ,проекция ускорения  По второму закону Ньютона  где - постоянный коэффициент. Таким образом, для того чтобы материальная точка совершала гармонические колебания, действующая на нее сила должна быть пропорциональна и направлена в сторону, противоположную смещению . Такая сила называется упругой (или в общем случае - квазиупругой).Рассмотрим систему, состоящую из груза массой , подвешенного на пружине, массой которой можно пренебречь (рис.3). Пусть - длина пружины без подвешенного к ней груза, тогда под тяжестью груза пружина растянется на  . В положении равновесия модуль силы тяжести равен модулю упругой силы  :  , где - коэффициент упругости пружины.Если вывести груз из положения равновесия 0, то на груз будет действовать дополнительная сила упругости, проекция которой на направленную вниз ось будет равна  (закон Гука). Под действием этой силы груз, после смещения на  и предоставленный самому себе, будет совершать гармонические колебания. Основное уравнение динамики поступательного движения (второй закон Ньютона) для груза принимает вид (4)Решение этого уравнения имеет вид  (5)Функция (5) - это закон движения груза на пружине, где - амплитуда колебания, т.е. наибольшее отклонение груза от положения равновесия. Подставляя решение (5) в (4), получаем Отсюда собственная частота системы  Так как  , то В рассмотренном примере не учитывалась сила сопротивления, поэтому колебания считались незатухающими. Затухающие колебания. Во всякой реальной колебательной системе имеются силы сопротивления, под действием которых колебания будут затухать. При достаточно малых скоростях движения сила сопротивления  пропорциональна скорости  ( - коэффициент сопротивления среды): или в проекции на ось : Знак минус обусловлен тем, что сила и скорость имеют противоположное направление.По второму закону Ньютона найдем уравнение затухающих колебаний:  (6)Решением уравнения движения (6) является функция (закон движения)  (7)Постоянные 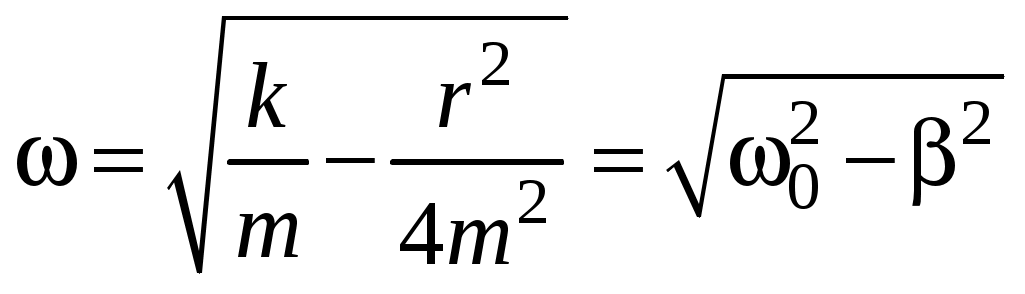и  могут быть любыми, в зависимости от начальных условий движения. Отметим, что - это начальная амплитуда; - коэффициент затухания;  - фаза колебания, а - начальная фаза колебания,  , где , а  . Коэффициент характеризует скорость затухания колебаний, т.е. уменьшение амплитуды за единицу времени.Если коэффициент затухания системы очень большой, то может выполниться условие 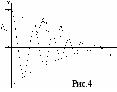 . В этом случае гармонических колебаний не возникнет, а будет наблюдаться апериодическое движение груза. На рис.4 представлен график зависимости от для затухающих колебаний.Быстроту затухания в зависимости от числа колебаний характеризуют логарифмическим декрементом затухания. Логарифмический декремент затухания равен натуральному логарифму отношения двух соседних амплитуд одного знака:  .Если известна - начальная амплитуда и - амплитуда через периодов (или через полных колебаний), то логарифмический декремент затухания .Коэффициент затухания характеризует затухание колебаний за единицу времени, а логарифмический декремент затухания - затухание колебаний за период, следовательно:  Контрольные вопросы 1. Каковы необходимые условия для возбуждения гармонических колебаний в механической системе? 2. Чем определяется период, амплитуда и начальная фаза свободных механических гармонических колебаний? 3. При каком условии колебания данного пружинного маятника не будут возбуждаться, движение его будет апериодическим? 4. Каков физический смысл коэффициента упругости пружины? 5. Каков физический коэффициента затухания, логарифмического декремента затухания? Как они связаны друг с другом? 6. Записать динамические уравнения и законы движения груза на пружине. 7. Получить формулу периода колебаний пружинного маятника. Литература 1. Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.VII, пар.50, 53, 58 Лабораторная работа 13 |
, с2
, с
, с
, мм