Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Определение коэффициента вязкости жидкости по методу CтоксаЦель работы: познакомиться с явлением внутреннего трения и определить коэффициент внутреннего трения (динамический коэффициент вязкости) по методу Стокса. Выполнение работы. 1. Измерить микрометром диаметр d шарика в миллиметрах (мм) и определить его радиус в метрах (м). 2. Осторожно отпустить шарик по центру сосуда непосредственно над поверхностью исследуемой жидкости и определить с помощью секундомера время t прохождения шарика между металлическими кольцевыми метками на сосуде. Верхняя метка должна находиться не менее десяти сантиметров от поверхности жидкости. 3. Определить по масштабной линейке расстояние  между метками и вычислить скорость шарика  (вычислить в СИ).4. Опыт повторить еще с четырьмя шариками. 5. Вычислить динамический коэффициент вязкости в СИ по формуле (2) в каждом опыте и найти среднее значение  .6. Результаты опытов и расчетов занести в таблицу.
 ...Плотность исследуемой жидкости 1 = l,2103 кг/м3; плотность свинца 2 = 11,4103 кг/м3. 7. Определить случайные отклонения  каждого измерения и среднее квадратичное отклонение  . Вычислить погрешность  результата измерений:  8. Записать результат в виде:  Пас.Теоретическое описание. 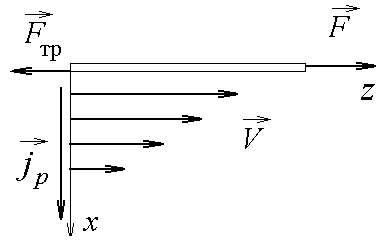 Рис.1 Неоднородное течение жидкости, т.е. такое, при котором скорость течения различна в разных местах, не является равновесным. Поэтому в жидкости будут происходить процессы, стремящиеся выровнять скорость течения. Такие процессы называются вязкостью или внутренним трением. Предположим, что жидкость всюду течет в направлении оси z , а значение скорости v меняется только в направлении х , перпендикулярном течению (рис.1). Тогда в направлении оси х возникает поток импульса. Импульс, переносимый за 1с через единичную площадку, перпендикулярную оси х, называется плотностью потока импульса и обозначается  .Из общих соображений следует, что пропорциональна градиенту скорости течения н направлена против градиента, т.е. , (1)где – коэффициент вязкости среды. Рассмотрим теперь вязкий поток, возникающий в жидкости под действием касательной силы, стремящейся сместить один слой молекул относительно другого (рис.2). Пусть f - сила, действующая на единицу поверхности, а -расстояние между соседними слоями. Тогда на одну молекулу будет действовать сила, равная f/n, где n –концентрация молекул. При перемещении молекулы в активированное состояние (рис.3) сила f/n с 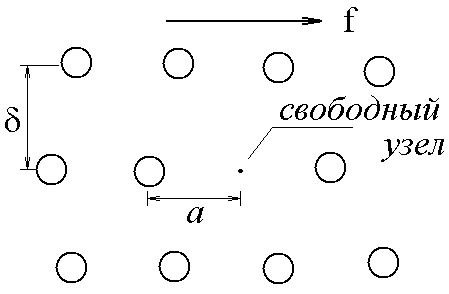 Рис.2 овершает работу, равную 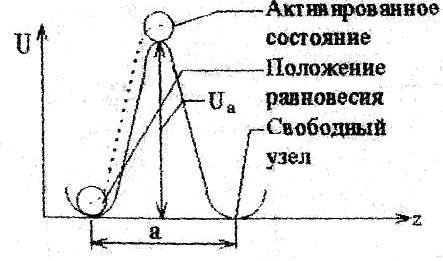 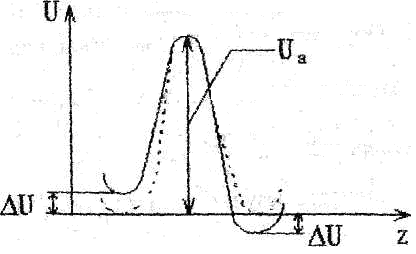, поэтому потенциальный барьер слева от активированного состояния уменьшается на величину этой работы (внешняя сила «помогает» молекуле совершить скачок в прямом направлении), а справа, наоборот. увеличивается (внешняя сила «препятствует» молекуле совершить обратный скачок). Эта ситуация изображена иа рис.4, где  .  Рис.3 Рис.4. Поэтому при наличии внешней силы частоты перескоков в свободную ячейку 1 и обратного перескока 2 будут неодинаковы, и в результате возникает поток молекул в направлении приложенной силы, скорость которого 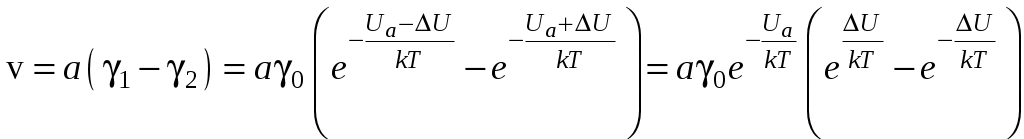 В результате переноса импульса (в направлении х) в жидкости возникают касательные по отношению к течению силы вязкого трения  , (2)где S – площадь, на которую действует  .Известно, что вязкость газов с ростом температуры растет, тогда как вязкость жидкостей убывает. Это различие обусловлено качественно разным характером теплового движения молекул газа и жидкости. По своей структуре жидкость ближе к кристаллическим твердым телам, чем к газам. Тепловое движение молекул жидкости сводится к колебаниям около некоторых положений равновесия (узлов), которые в отличие от положений равновесия в кристаллах носят временный характер –через некоторое время (время релаксации) молекула жидкости скачком переходит в новое, свободное положение равновесия. Чтобы совершить этот переход, молекула должна преодолеть потенциальный барьер, высота которого Ua называется энергией активации (рис.3). Частота таких переходов определяется распределением Больцмана:  (3)где 0 – некоторая константа. Очевидно, что в отсутствие внешних сил частоты переходов в прямом и обратном направлениях будут одинаковыми и никакого результирующего течения не возникает. Так как обычно  и  , то  .С учетом того, что 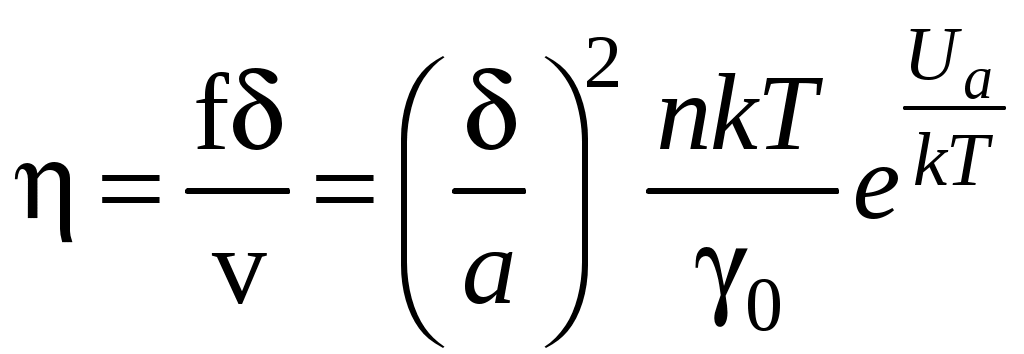 , получаем выражение для коэффициента вязкости в виде  .Как показывают расчеты,  , где h – постоянная Планка. Полагая также  , получим окончательное выражение для коэффициента вязкости жидкости: (4)Как следует из формулы (4), вязкость жидкости резко (экспоненциально) убывает с ростом температуры. Кроме того, вязкость сильно зависит от вида жидкости и от ее чистоты. Действие сил внутреннего трения легко наблюдать при движении тела в жидкости. При малых скоростях и удобообтекаемой форме тела, когда не возникает вихрей, сила сопротивления обусловлена исключительно вязкостью жидкости. Слой жидкости, непосредственно прилегающий к твердому телу, увлекается им полностью. Следующий слой увлекается за телом с меньшей скоростью. Таким образом, между слоями возникают силы сопротивления. Для небыстрого движения шарика в жидкости Стокс вывел путем теоретического рассмотрения формулу расчета силы сопротивления:  (5)где – динамический коэффициент вязкости;  –радиус шарика; v – скорость его движения относительно жидкости.Предоставим маленькому шарику возможность падать в жидкость под действием силы тяжести. На него будут действовать следующие силы (рис.5): 1. Сила тяжести, направленная по вертикали вниз  г 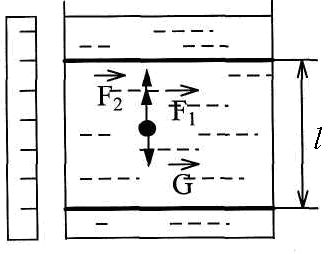 Рис.5 де  – плотность шарика, g - ускорение свободного падения.2. Выталкивающая сила F1, являющаяся результатом гидростатического давления. Она направлена по вертикали вверх и равна по закону Архимеда силе тяжести жидкости в объеме тела:  , где  – плотность жидкости.3. Сила внутреннего трения F2 . Она направлена против направления скорости шарика, т.е. вертикально вверх. По формуле Стокса  Силы G и F1 постоянны, а сила F2 увеличивается по мере увеличения скорости шарика. При некоторой скорости v наступает момент, когда сила G, направленная вниз, будет уравновешена силами F1 и F2 , направленными вверх; с этого момента шарик будет двигаться равномерно, в соответствии с первым законом Ньютона. Скорость равномерного падения невелика, если шарик мал, и ее легко измерить. Тогда из условия равновесия сил  можно определить динамический коэффициент вязкости  (6)Контрольные вопросы. 1. Написать общее вьфажение для вязкой силы и проиллюстрировать чертежом. 2. Дать определение динамического коэффициента вязкости. Какова единица его измерения в СИ? 3. Какие силы действуют на шарик, движущийся в глицерине? 4. Почему риска 1 должна находиться несколько ниже поверхности жидкости? 5. Вывести расчетную формулу динамического коэффициента вязкости г|. 6. Как вязкость жидкости зависит от температуры? Литература. 1. Савельев И.В. Курс физики. Т.1 - М., Наука, 1989. 352 с. Пар. 78,79 Лабораторная работа № 16 |