Методические указания по выполнению лабораторных работ по механике и молекулярной физике, входящих в первую часть физического практикума по дисциплине "Физика"
 Скачать 2.35 Mb.
|
Определение коэффициента поверхностного натяжения воды методом отрыва кольцаЦель работы: измерить коэффициент поверхностного натяжения воды при комнатной температуре. Описание установки.  Рис.1 Установка состоит из пружины 1, к которой подвешено легкое алюминиевое кольцо 3 с тонкими стенками и чашкой 2 наверху, масштабной линейки 5 и сосуда 4 с дистиллированной водой (рис.1).  Рис. 2 Если сосуд с водой подвести к кольцу до соприкосновения, а затем плавно опускать, то жидкость, сцепившись с кольцом, будет тянуть его за собой, растягивая пружину до тех пор, пока кольцо не оторвется от жидкости. В момент перед самым отрывом наступает равновесие, когда и кольцо, и жидкая пленка покоятся. В этот момент сила упругости пружины равна силе поверхностного натяжения. Поверхностная пленка будет иметь вид, показанный на рис. 2., где  – сила поверхностного натяжения, действующая на элемент контура. Модуль полной силы (1)где  и  – длины двух контуров (окружностей), ограничивающих поверхность жидкости. Так как  ,  , где  и  – внешний и внутренний диаметры кольца, то из (1) получаем  (2)Порядок выполнения работы. 1. Штангенциркулем измерить наружный и внутренний диаметры кольца в пяти местах. Данные занести в таблицу 1.2. Подвесить кольцо к пружине. 3. Определить по шкале положение  верхней части чашки 2 над кольцом в ненагруженном состоянии (F=0). Смотреть на шкалу нужно так, чтобы передний верх чашки совпал с задним. Об этом не следует забывать до конца эксперимента.4. Взять одну гирьку (цифры на каждой гирьке указаны в миллиграммах), поместить в центр чашки 2 и определить по шкале положение  ее верхнего края.5. Увеличивая нагрузку F (последовательно добавляя по одной гирьке, не забывайте подсчитывать общую сумму нагрузки в миллиграммах), определять по шкале положение  верхнего края чашки 2. Данные измерений занести в табл. 2.6. Снять все гирьки с чашки. 7. Поднимать сосуд 4 с водой до тех пор, пока поверхность воды не коснется нижнего края кольца. Следить за тем, чтобы этот край только смачивался, но не опускался вглубь воды. Затем, медленно и равномерно опуская сосуд, уловить равновесие (система находится в покое) перед отрывом кольца и заметить по шкале положение  верхнего края чашки. Измерения проделать не менее 5 раз и найти среднее арифметическое значение  . Данные занести в таблицу 1. Рис.3 8. Осторожно снять кольцо с пружины и положить на установку. 9. Построить график градуировки пружины  , принимая за начало координат значение . Вид графика представлен на рис.3.10. Зная растяжение пружины под действием силы поверхностного натяжения, по построенному графику определить ее значение  в миллиграммах, а затем перевести в Ньютоны.11. Вычислить в СИ коэффициент поверхностного натяжения воды . Таблица 1
Таблица 2
Теоретическое описание.  Рис.4 Жидкости обладают поверхностным слоем, состоящим из молекул, обладающих большей потенциальной энергий, чем внутренние молекулы. Между молекулами действуют силы притяжения, очень быстро убывающие с расстоянием, поэтому возле каждой молекулы можно очертить сферу молекулярного действия так, что выделенная молекула будет взаимодействовать только с молекулами, оказавшимися внутри этой сферы (рис.4). Если молекула находится внутри жидкости, то она взаимодействует с молекулами-соседями, окружающими ее со всех сторон, и результирующая сил притяжения равна нулю (а и b на рис.4). Наоборот, молекула, находящаяся на поверхности жидкости (d на рис.4), окружена молекулами-соседями лишь наполовину и на нее действует нескомпенсированная сила, направленная перпендикулярно к поверхности внутрь жидкости. Такая же сила, только поменьше, действует и на любую другую молекулу, оказавшуюся внутри слоя толщиной, равной радиусу молекулярного действия (с на рис.4). Следовательно, поверхностный слой оказывает давление на остальную жидкость (давление называют внутренним) и оно достигает очень больших величин. Это, в свою очередь, означает, что поверхностный слой обладает избыточной (по сравнению с остальной жидкостью) энергией, которую называют поверхностной. Очевидно, что поверхностная энергия пропорциональна числу молекул в поверхностном слое, т.е. площади поверхности жидкости S: = Uпов=S (3) Коэффициент пропорциональности , численно равный поверхностной энергии, приходящейся на единицу площади поверхности, называется коэффициентом поверхностного натяжения. Известно также, что в состоянии устойчивого равновесия любая система обладает минимальной потенциальной энергией. Поэтому поверхностный слой стремится принять такую форму, при которой его поверхность будет наименьшей (тогда и Uпов достигает минимума, как это следует из формулы (3). Если же искусственно увеличивать поверхность жидкости, то в поверхностном слое возникают силы, препятствующие этому, – они называются силами поверхностного натяжения Таким образом, поверхностный слой похож на упругую пленку, как будто бы находящуюся на поверхности жидкости. 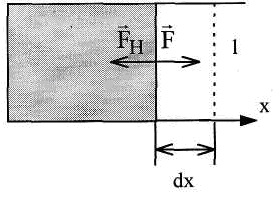 Рис.5 Рассмотрим пример. Пусть жидкая (мыльная) пленка ограничена прямоугольной проволочной рамкой, одна из сторон которой длиною  может перемещаться вдоль оси Х (рис.5) под действием внешней силы  . Этой силе будет противодействовать сила поверхностного натяжения  . В случае квазистатического (медленного) процесса  . При перемещении на  сила F совершает работу  , а потенциальная энергия поверхности увеличивается на  . Так как  , то  и (4) Рис.6 Формула (4) позволяет по-другому определить , а именно как силу поверхностного натяжения, приходящуюся на единицу длины контура ограничивающего поверхность. Из этого же примера видно, что сила поверхностного натяжения направлена по касательной к поверхности и перпендикулярна к линии, ограничивающей поверхность (рис. 6). Контрольные вопросы. 1. Как объяснить стремление жидкости сократить свою свободную поверхность? 2. На что затрачивается работа при увеличении поверхности жидкости? 3. Дать два определения коэффициента поверхностного натяжения. Единицы его измерения. 4. Вывести расчетную формулу коэффициента поверхностного натяжения. 5. Как направлена сила поверхностного натяжения в момент отрыва кольца? 6. Как и от чего зависят силы молекулярного взаимодействия и коэффициент поверхностного натяжения? 7. Можно ли определить коэффициент поверхностного натяжения методом отрыва кольца, если жидкость не смачивает кольцо? Литература. 1. Савельев И.В. Курс физики. Т.1 - М., Наука, 1989. 352 с. Пар. 92,93,94. Лабораторная работа № 15 | ||||||||||||||||||||||||||||||