метод наименьших квадратов. Методические указания по выполнению лабораторной работы Хабаровск Издательство двгупс 2002 удк 517. 518. 87 (075. 8) Ббк в 191. 1я73
 Скачать 0.58 Mb.
|
2. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИИЙ.Пусть функция  задана таблицей, полученной в результате наблюдений.Таблица 2.1
Требуется найти алгебраический полином   возможно низшей степени так, чтобы значение полинома в заданных точка  совпадает со значениями функции  в этих точках, то есть  ,  Т   акой полином называется интерполяционным. Если  , то существует единственный полином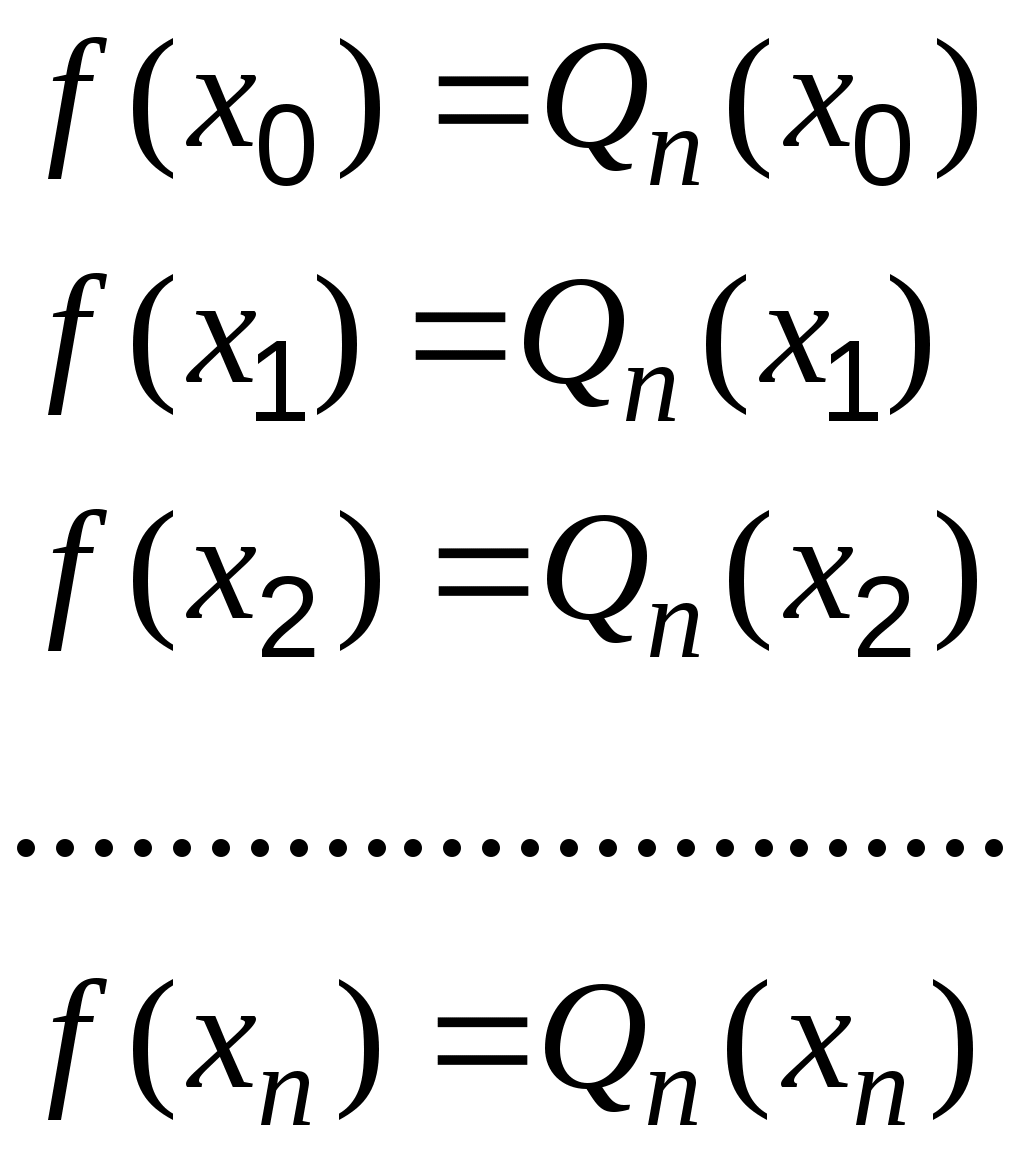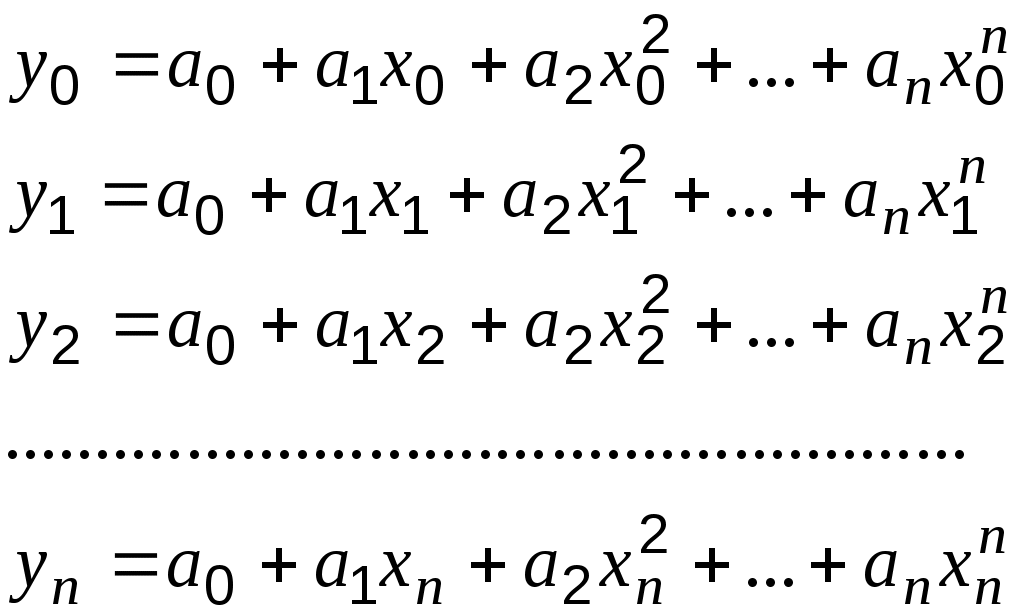, полученный из решения системы   Определитель этой системы, называемый определителем Вандермонда, отличен от нуля, поэтому система имеет единственное решение. 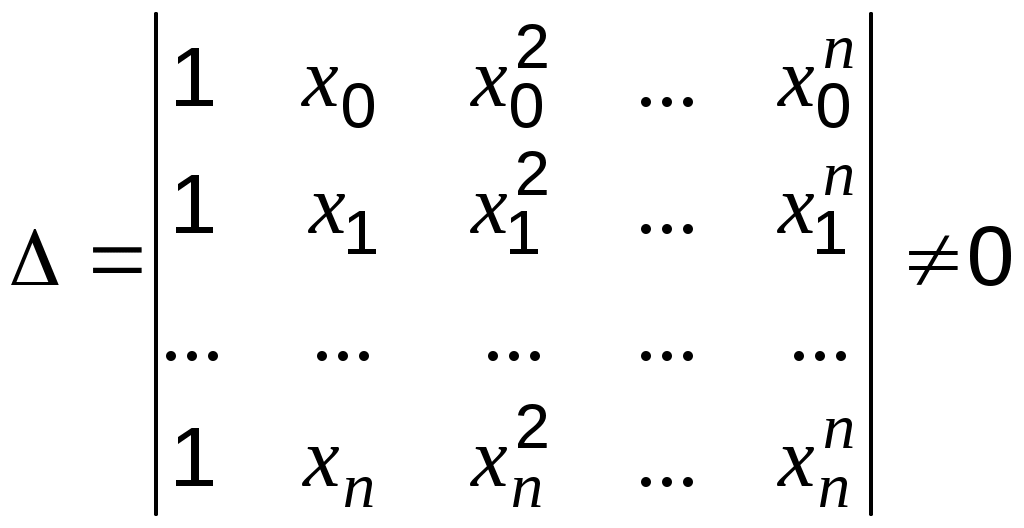 Полином, коэффициенты которого получены решением указанной системы, называется интерполяционным полиномом Лагранжа, определяемым формулой:  Если  , то интерполяционный полином Лагранжа может быть записан в виде интерполяционного многочлена Ньютона:   ,где  Выражения  называются конечными разностями  -го порядка.Интерполяционный многочлен Ньютона тождественно совпадает с интерполяционным многочленом Лагранжа. Точки  называют узлами интерполяции. Полученные полиномы позволяют приближённо восстановить значение функции  в произвольных точках между узлами интерполяции. Если точка  расположена вне отрезка, содержащего все узлы интерполяции, то замена функции полиномом называется задачей экстраполяции.У интерполяционного многочлена Лагранжа видна его явная зависимость от каждого значения  , поэтому при изменении количества узлов интерполяции (уменьшении или увеличении) приходится строить многочлен заново.Интерполяционный многочлен Ньютона выражается не через значения функции, а через её конечные разности, поэтому при изменении степени n требуется только добавить или отбросить соответствующее число стандартных слагаемых. |
