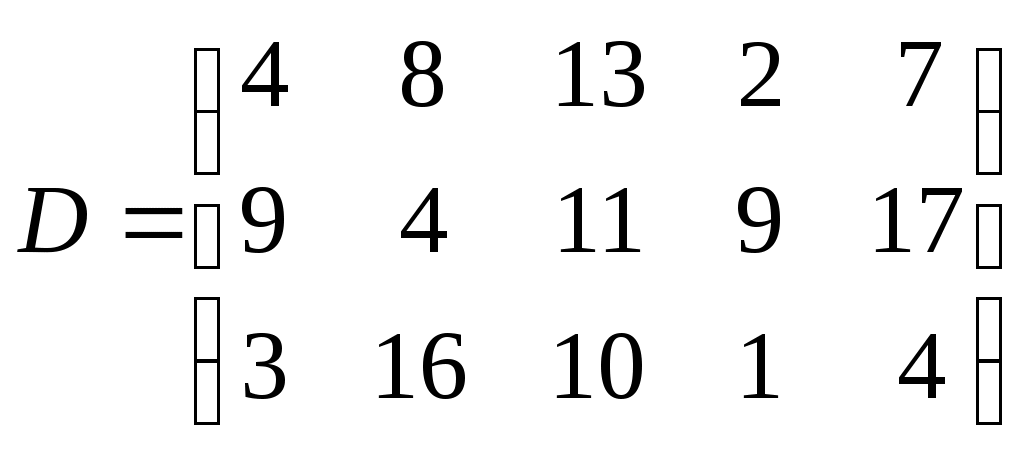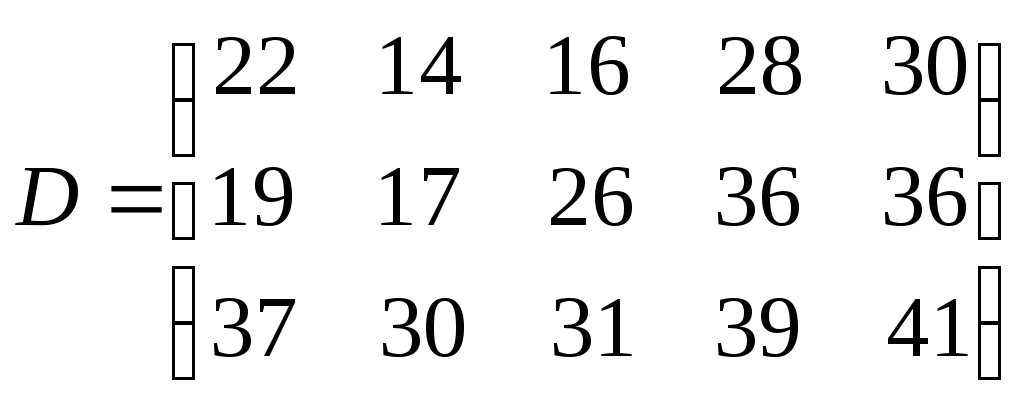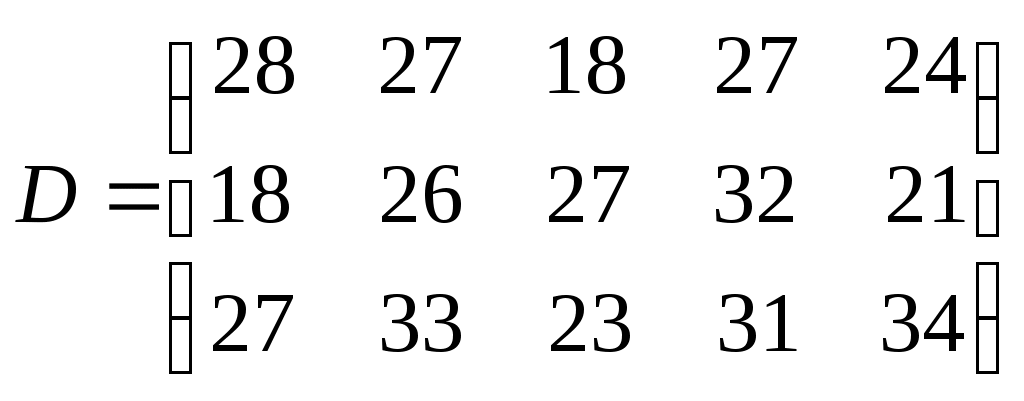ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb.
|
|
Рис. 3. Обобщенная схема математической модели По способу реализации математические модели можно разделить следующим образом. 1. Линейное программирование. Математическая модель целиком (целевая функция и ограничения) описывается уравнениями первого порядка. Линейное программирование включает в себя несколько методов решения (задач): симплексный; графический; транспортная задача; целочисленное программирование. 2. Нелинейное программирование. Целевая функция и ограничения, составляющие математическую модель, содержат хотя бы одно нелинейное уравнение (уравнение второго порядка и выше). Нелинейное программирование содержит несколько методов решения (задач): графический; регулярного симплекса; деформируемого многогранника (Нелдера - Мида); градиентный. 3. Динамическое программирование. Ориентировано на решение задач прокладки магистралей кратчайшим путем и перераспределения различных видов ресурсов. 4. Сетевое планирование. Решает проблему построения графика выполнения работ, распределения производственных, финансовых и людских ресурсов. 5. Принятие решений и элементы планирования. В этом случае и качестве целевой функции выступает набор статистических данных или некоторые данные прогноза. Решением задачи являются рекомендации о способах поведения (стратегии). Решение носит рекомендательный характер (приблизительное решение). Выбор стратегии целиком остается за человеком — ответственным лицом, принимающим решение. Для принятия решения разработаны следующие теории: теория игр; системы массового обслуживания. Порядок выполнения заданий Задание 1. Составить математическую модель следующей задачи. На складе имеется 300 кг сырья. Надо изготовить два вида продукции. На изготовление первого изделия требуется 2 кг сырья, а на изготовление второго изделия — 5 кг. Определить план выпуска двух изделий. Решение. Обозначим, х1 – единица первого изделия, х2 – единица второго изделия. Тогда составим математическая модель: 2х1+5х2=300. Задание 2. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал 3-х сортов. При этом на изготовление единицы изделия вида А расходуется 14 кг первого сорта, 12 кг второго сорта и 8 кг третьего сорта. На изготовление продукции вида В расходуется 8 кг первого сорта, 4 кг второго сорта, 2 кг третьего сорта. На складе фабрики имеется всего материала первого сорта 624 кг, второго сорта 541 кг, третьего сорта 376 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида 7 руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида 3 руб. Определить максимальную прибыль от реализации всей продукции видов А и В. Решение. Составим математическую модель задачи: Пусть х1 – единица готовой продукции вида А, x2 - единица готовой продукции вида В, Цель фабрики получить максимальную прибыль от реализации всей продукции видов А и В, тогда:  Система ограничений: 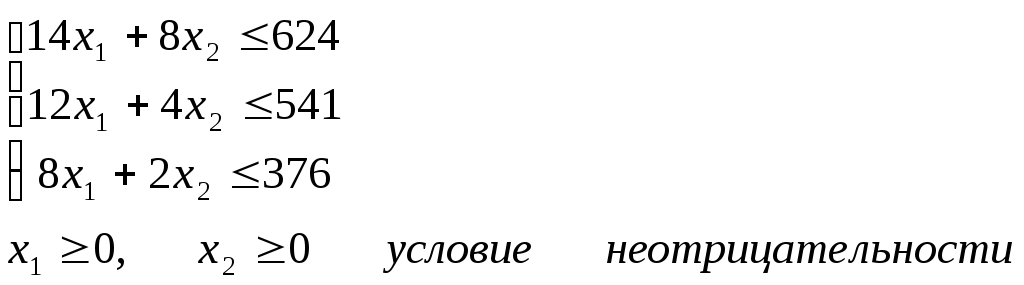 Задание 3. Составить математическую модель следующей задачи. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве 200, 450, 250 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно 100, 125, 325, 250, 100 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Решение: Проверка сбалансированности модели задачи. Модель является сбалансированной, т.к. суммарный объем запасов сырья равен суммарному объему потребности в ней: 200+450+250=100+125+325+250+100. Построение математической модели – неизвестными в этой задачи является объем перевозок. Пусть  - объем перевозок с i-го предприятия в j-го пункт потребления. Суммарные транспортные расходы - это функционал качества (критерий цели):  ,Где  - стоимость перевозки единицы продукции с i-го предприятия в j-й пунктах потребления.Неизвестные в этой задачи должны удовлетворять следующим ограничениям: Объем перевозок не могут быть отрицательными; Поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятия, а потребность всех пунктов потребления должна быть полностью удовлетворены. Итак, имеем следующую задачу: Найти минимум функционала:  При ограничениях: 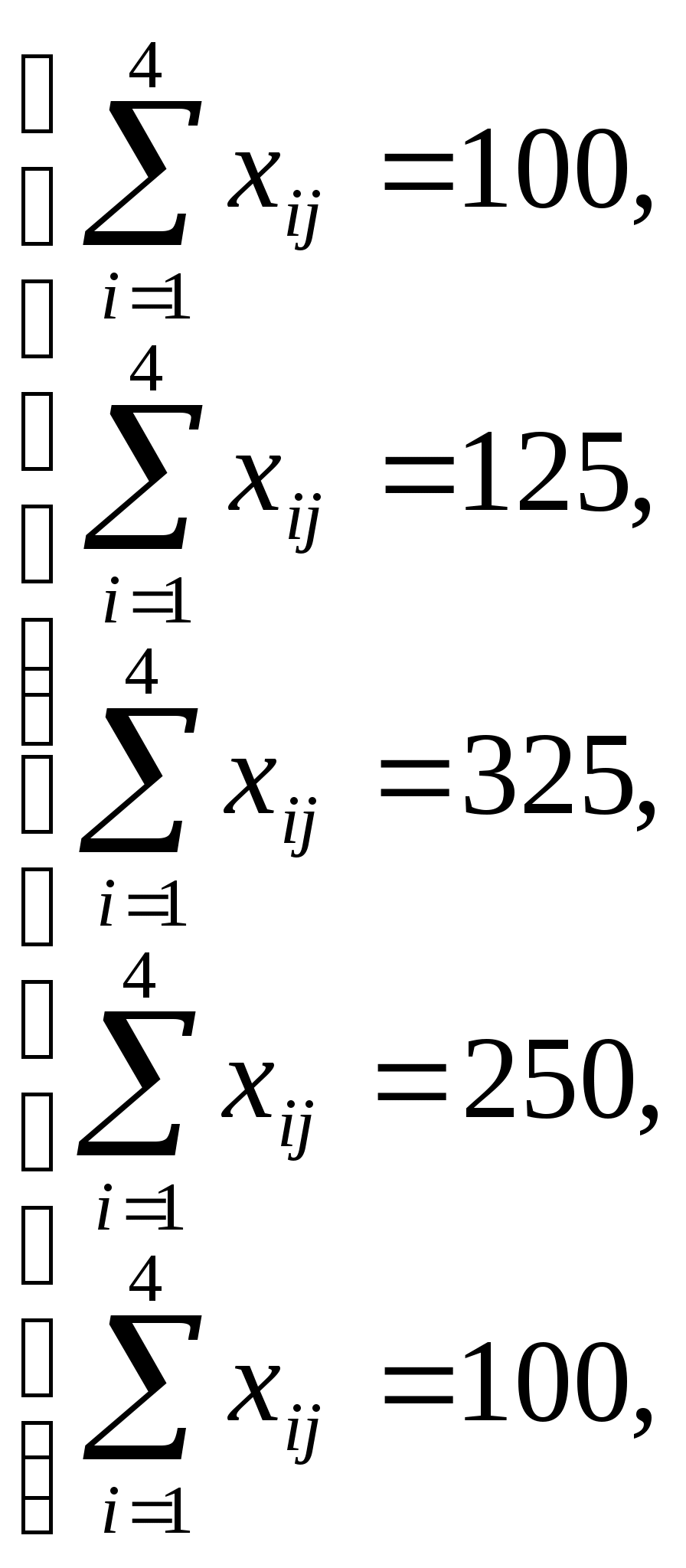 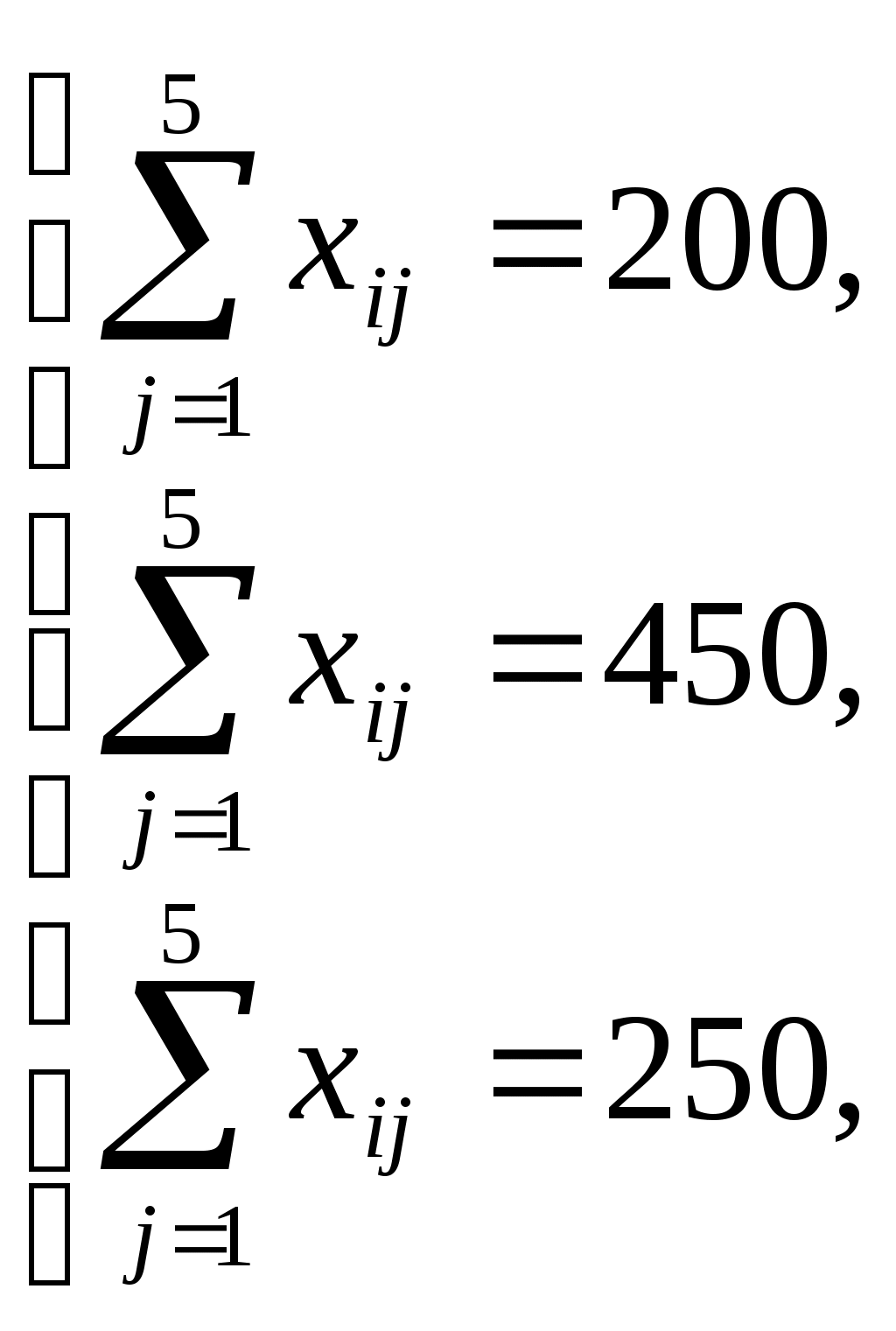  ,Задания для самостоятельной работы 1 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 19, а2= 16, а3= 19, b1= 26, b2= 17, b3= 8, c1= 868, c2= 638, c3= 853, α=5, β=4. Задача 2. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
2 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 14, а2= 15, а3= 20, b1= 40, b2= 27, b3= 4, c1= 1200, c2= 993, c3= 1097, α=5, β=13. Задача 2. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
3 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 9, а2= 15, а3= 15, b1= 27, b2= 15, b3= 3, c1= 606, c2= 802, c3= 840, α=11, β=6. Задача 2. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
