ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
Муниципальное образовательное учреждение среднего профессионального образования Саянский муниципальный колледж экономики и управления Утверждаю Директор КЭиУ _________ Урбагаева М.К. «____»_________200__ Методические указания по выполнению практических работ по дисциплине «Математические методы» для студентов специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем г. ____________200 г.
Курмель Е.А., Методические указания по выполнению практических работ по дисциплине «Математические методы». Саянское муниципальное образовательное учреждение среднего профессионального образования «Колледж экономики и управления», 2009г.Методические указания предназначены для студентов специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем. Рассматриваются прикладные математические методы и модели, в том числе методы математического программирования (поиск экстремума, линейное, нелинейное, динамическое программирование), алгоритмы на графах, системы массового обслуживания, имитационное моделирование, прогнозирование. Приведено подробное описание всех алгоритмов решения задач, даны пояснения и примеры решения различных задач. Разработана группа заданий и список контрольных вопросов на каждую практическую работу для индивидуальной работы студентов, а также имеется список рекомендуемой литературы для самостоятельного изучения. Разработал преподаватель____________________________________________ Ф.И.О. Содержание
Введение Данные методические указания по выполнению практических работ по дисциплине «Математические методы» содержат краткую теоретическую часть, в которой изложены основные прикладные математические методы и модели, в том числе методы математического программирования (поиск экстремума, линейное, нелинейное, динамическое программирование), алгоритмы на графах, системы массового обслуживания, имитационное моделирование, прогнозирование. Разобраны примеры решения задач, варианты индивидуальных заданий, предназначенные не только для повторения теории, но и для индивидуальной или самостоятельной работы студента и контрольные вопросы. Проблема выполнения различных вычислений была актуальна во все времена. По мере развития общественно-экономических отношений усложнялись поставленные задачи, которые для своего решения требовали разработки новых методов вычислений. На смену простейшим арифметическим и геометрическим вычислениям пришли алгебраические и тригонометрические вычисления. Организация современного производства требует не только наличия современных станков и оборудования, но и разработки новых технологических процессов и современных методов управления производством. Для решения каждой из поставленных задач разрабатываются математические модели, анализируя которые удается найти наилучшее решение поставленной задачи. Создание математической модели — сложная и кропотливая работа, которая в современных условиях под силу коллективам разработчиков. Для создания математической модели одного и того же объекта различные коллективы могут использовать различный математический аппарат. В коллектив разработчиков математических моделей привлекаются высококвалифицированные специалисты, которые, с одной стороны, хорошо знают физические процессы, протекающие при работе объекта, и, с другой стороны, глубоко и всесторонне владеют соответствующим математическим аппаратом. После создания математической модели специалистами-аналитиками за дело принимаются специалисты-программисты, которые реализуют созданную модель в виде программных кодов. Далее с математической моделью работают специалисты-практики. Целенаправленно воздействуя на модель, они изучают ее поведение и подбирают оптимальный режим работы для реального объекта. Практическая работа №1 «Построение простейших математических моделей. Построение простейших статистических моделей» Цель работы: закрепить практические навыки по построению простейших математических и простейших статистических моделей. Краткая теория Построение математической модели процесса, явления или объекта начинается с построения упрощенного варианта модели, в котором учитываются только основные черты. В результате прослеживаются основные связи между входными параметрами, ограничениями и показателем эффективности. Общего подхода к построению модели нет. В каждом конкретном случае при построении математической модели учитывается большое количество факторов: цель построения модели, круг решаемых задач, точность описания модели и точность выполнения вычислений. Математическая модель должна отражать все существенные факторы, определяющие ее поведение, и при этом быть простой и удобной для восприятия результатов. Каждая математическая модель процесса, явления или объекта в своей основе имеет математический количественный метод. Применение математических количественных методов для обоснования выбора того или иного управляющего решения во всех областях человеческой деятельности называется исследованием операций. Целью исследования операций является нахождение с использованием специального математического аппарата решения, удовлетворяющего заданным условиям. На самом деле при решении практически любой задачи имеется неограниченное количество решений. Множество решений, удовлетворяющих заданным условиям (ограничениям), называется допустимым множеством решением. Выбор из множества допустимых решений одного решения, наилучшего в каком-либо смысле, называемого оптимальным решением, и есть задача исследования операций. Модель — это материальный или идеальный объект, заменяющий оригинал, наделенный основными характеристиками (чертами) оригинала и предназначенный для проведения некоторых действий над ним с целью получения новых сведений об оригинале. 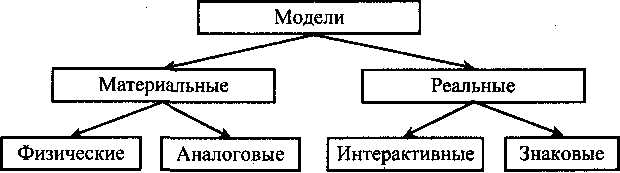 Рис. 1. Классификация моделей 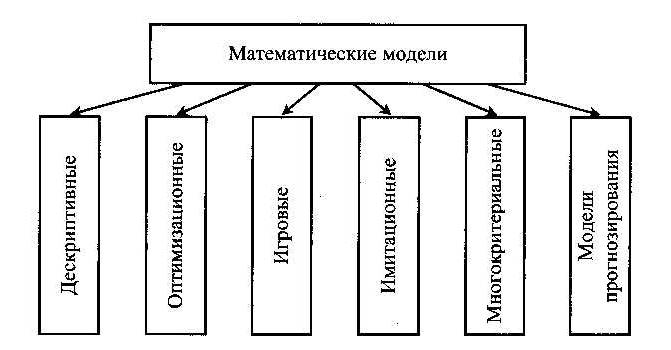 Рис. 2. Классификация математических моделей При построении математической модели необходимо обеспечить достаточную точность вычислений (точность решения) и необходимую подробность модели. Любая математическая модель включает в себя описание основных, т. е. необходимых для исследования свойств и законов функционирования исследуемого объекта, процесса или явления. В своей основе каждая математическая модель имеет целевую функцию, которая описывает функционирование реального объекта, процесса или явления. В зависимости от исследуемого (моделируемого) объекта, явления или процесса целевая функция может быть представлена одной функциональной зависимостью, системой уравнений (линейных, нелинейных, дифференциальных и т. д.), набором статистических данных и т. д. При работе с целевой функцией исследователь воздействует на нее через набор входных параметров (рис. 3).
|
