ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
Замечание. Опорный план должен быть невырожденным. Алгоритм решения транспортной задачи: Строим начальные планы методом северо-западного угла и наименьшей стоимости, из них выбираем лучший. Находим потенциалы поставщиков и потребителей, используя первое условие оптимальности плана: Проверяем второе условие оптимальности плана для свободных клеток 4. Улучшение плана. a) при невыполнении второго условия оптимальности плана в клетку заносим нарушение среди всех потенциальных клеток выбираем клетку с наибольшим нарушением; строим для выбранной клетки замкнутый контур, состоящий из вертикальных и горизонтальных отрезков прямой, причем вершины контура лежат в занятых клетках, за исключением той клетки, для которой строится контур. Виды контуров приведены на рисунке 1; 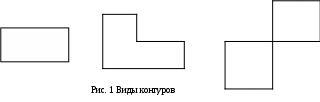 вершины контура поочередно помечаем, знаками "+","-", начиная с клетки, для которой построен контур; е) среди клеток, помеченных знаком "-", выбираем наименьшую перевозку. На эту величину увеличиваем перевозки в клетках, помеченных знаком "+", и уменьшаем вклетках, помеченных знаком "-". В результате переназначения перевозок освобождается одна клётка. 5.Вновь полученный план проверяем на оптимальность. Порядок выполнения заданий Задание. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
Решение. 1. Построим начальный план двумя методами: методом северо-западного угла и методом наименьшей стоимости, и выберем тот план, который будет наилучшим, то есть получим минимальные затраты за перевозку однородного груза. А) Строим начальный план методом северо-западного угла. Составим таблицу значений:
Число назначенных перевозок m+n-1=3+5-1=7, то есть начальный план При таком плане суммарные транспортные издержки равны: Б) Строим начальный план методом наименьшей стоимости. Составим таблицу значений:
Начальный план: При таком плане транспортные издержки Сравнивая транспортные издержки, видим, что план, построенный методом наименьшей стоимости, лучший. 2. Выбираем лучший план и находим потенциалы поставщиков и потребителей, используя первое условие оптимальности плана:
Используя первое условие оптимальности плана, составим систему линейных уравнений для определения потенциалов: 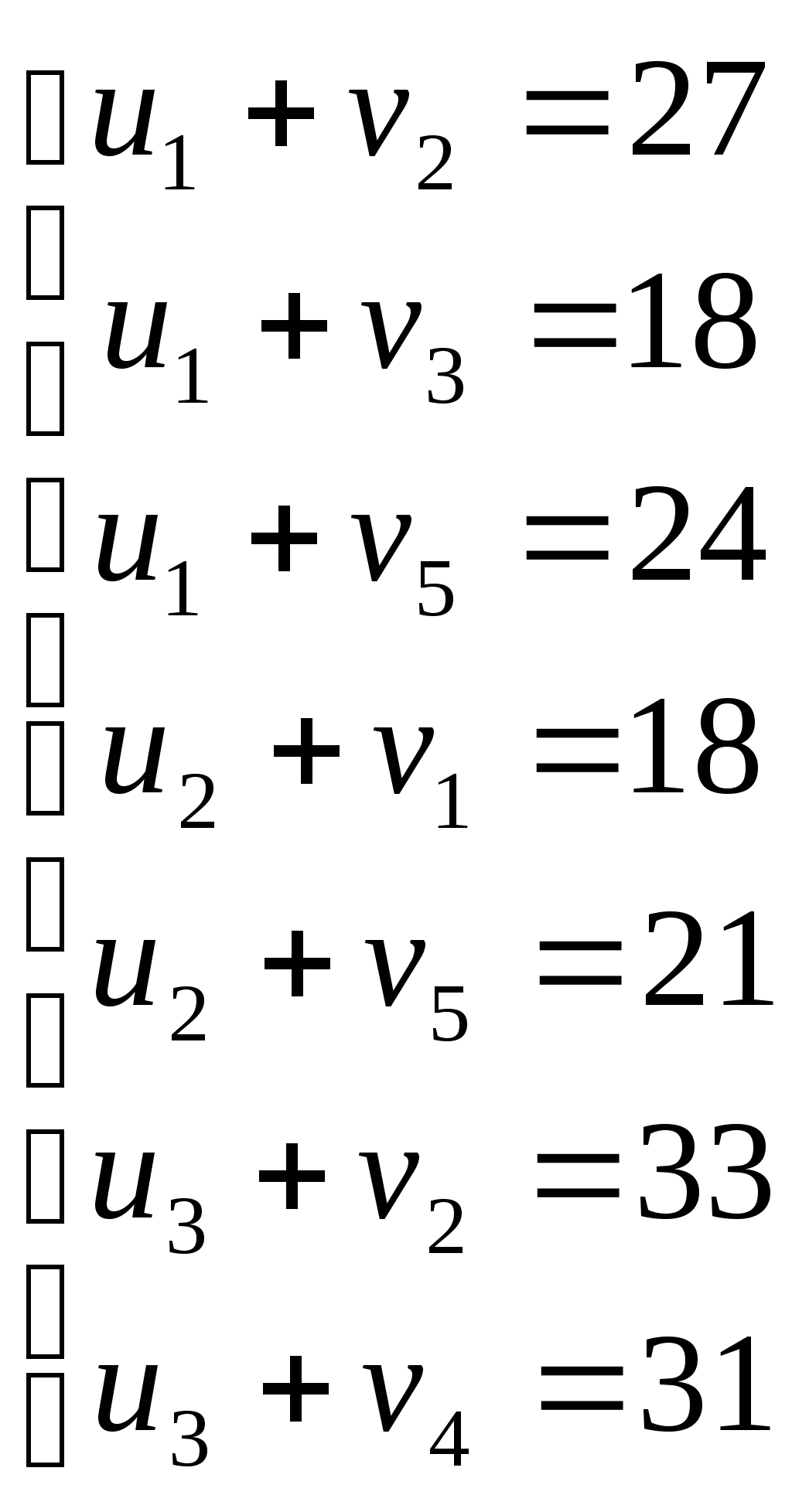 Система линейных уравнений содержит 7 уравнений и 8 неизвестных, т.е. она имеет множество решений. Так как нужно одно решение, то любой из неизвестных задаем значение и вычисляем остальные неизвестные. ■ Пусть Проверяем второе условие оптимальности плана для свободных клеток Улучшение плана. Выбираем клетку с максимальным нарушением и для нее строим замкнутый контур.
Среди клеток, помеченных знаком «-», выбираем наименьшую перевозку: На эту величину увеличиваем перевозки в клетках, помеченных знаком «+», и уменьшаем в клетках, помеченных знаком «-». В результате переназначения перевозок имеем план:
Используя первое условие оптимальности плана, составим систему линейных уравнений для определения потенциалов: 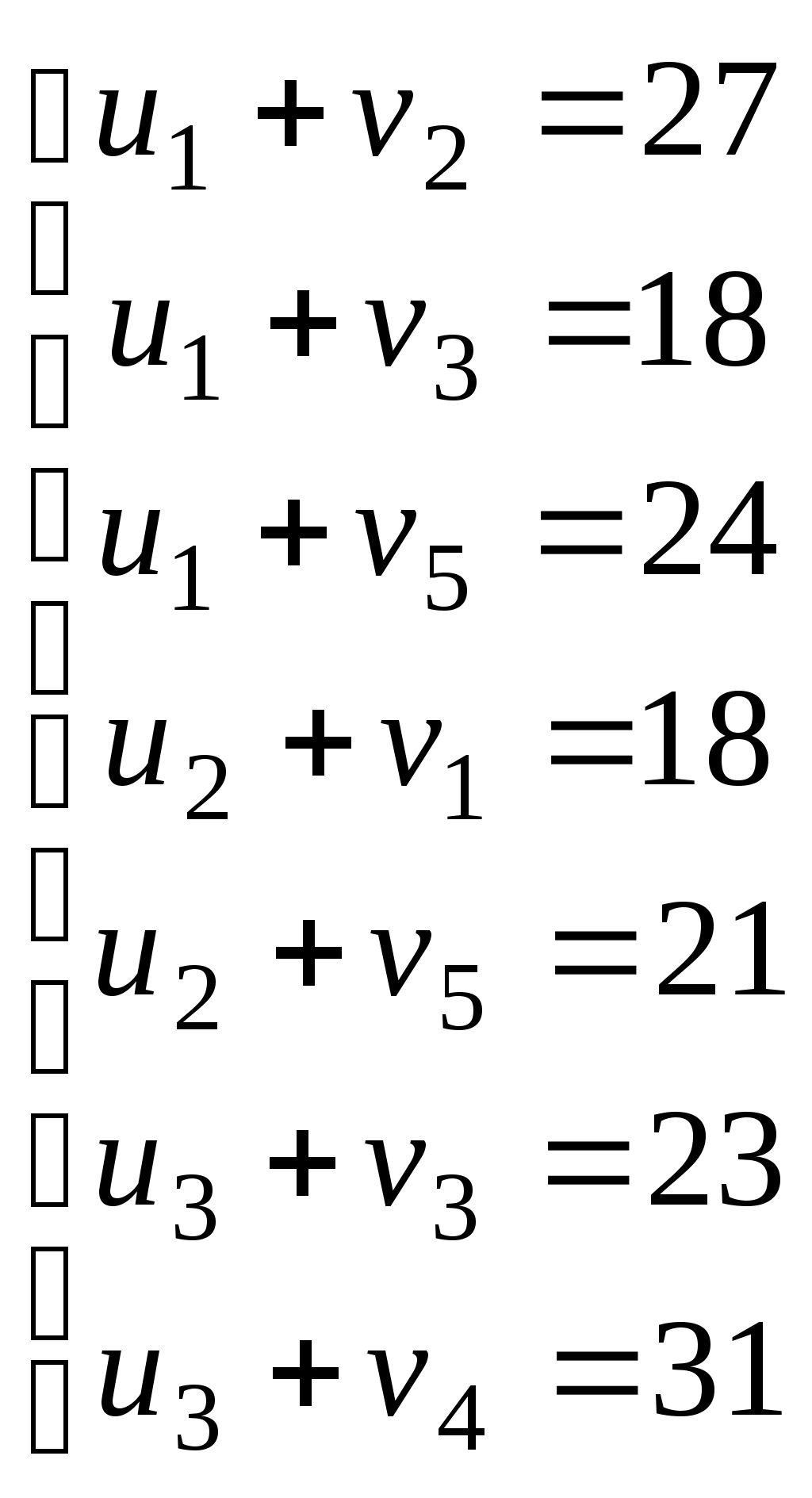 Система линейных уравнений содержит 7 уравнений и 8 неизвестных, т.е. она имеет множество решений. Так как нужно одно решение, то любой из неизвестных задаем значение и вычисляем остальные неизвестные. ■ Пусть Проверяем второе условие оптимальности плана для свободных клеток Ответ: Сравнивая три метода нахождения оптимального плана, делаем вывод, что метод потенциалов находит оптимальный план решения транспортной задачи, так как получили минимальные транспортные издержки равные 15080 единиц. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

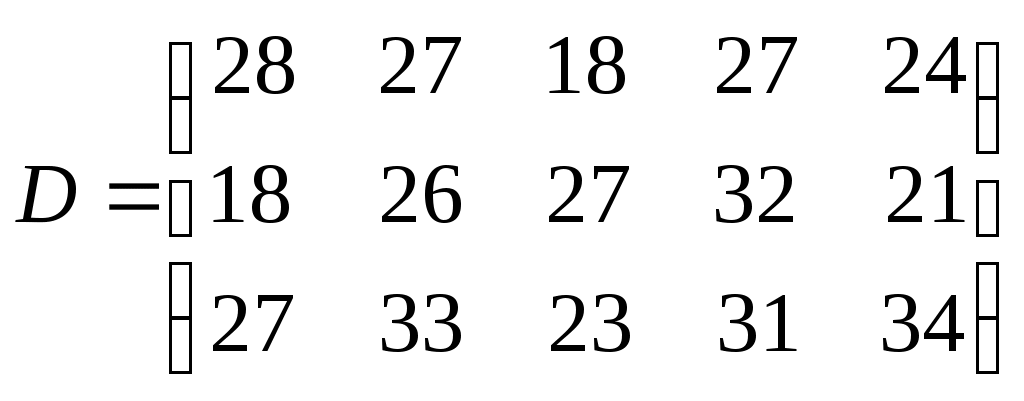

 10
10