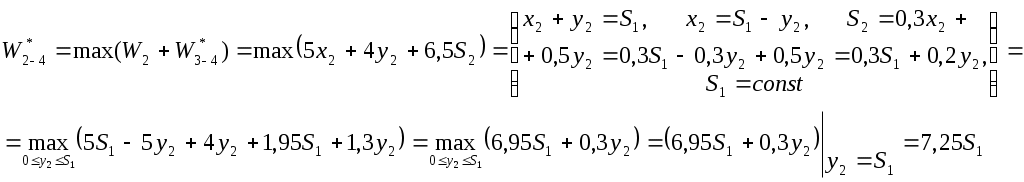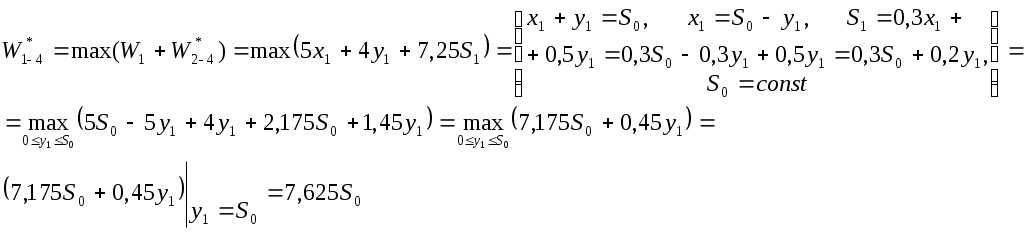|
|
ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
Задача определения кратчайших расстояний по заданной сети
Пусть дано конечное число точек 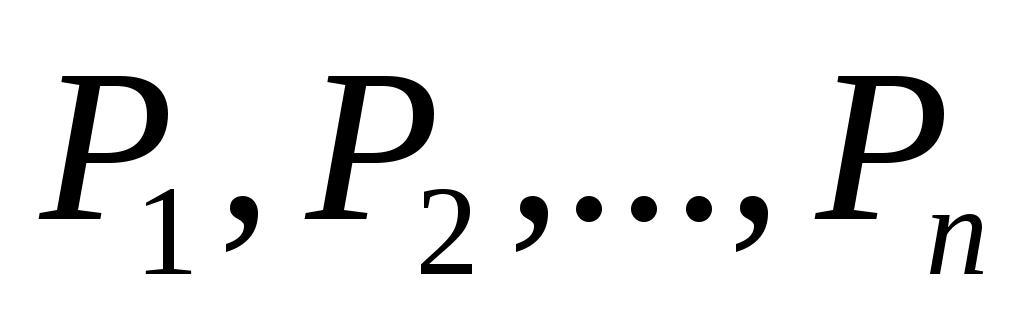 , соединенных всевозможными отрезками линий, называемых звеньями или связями. Тогда совокупность точек и их связей называют сетью. Сеть называется достаточно связанной, если существует путь, состоящий из звеньев и соединяющий любые две точки сети. Пусть каждому звену поставлено в соответствие действительное неотрицательное число , соединенных всевозможными отрезками линий, называемых звеньями или связями. Тогда совокупность точек и их связей называют сетью. Сеть называется достаточно связанной, если существует путь, состоящий из звеньев и соединяющий любые две точки сети. Пусть каждому звену поставлено в соответствие действительное неотрицательное число 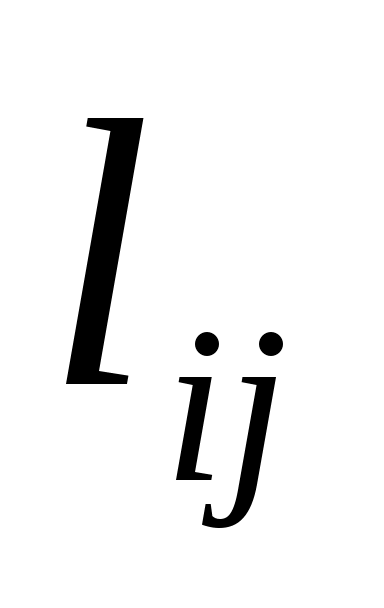 - его длина. Необходимо определить кратчайшее расстояние по сети от каждой точки до всех остальных и соответствующие пути, по которым, они проходят. Пронумеруем точки сети в любом порядке и укажем длину каждого звена. Две точки называются соседними, если они непосредственно соединены связью. Положим, - его длина. Необходимо определить кратчайшее расстояние по сети от каждой точки до всех остальных и соответствующие пути, по которым, они проходят. Пронумеруем точки сети в любом порядке и укажем длину каждого звена. Две точки называются соседними, если они непосредственно соединены связью. Положим, 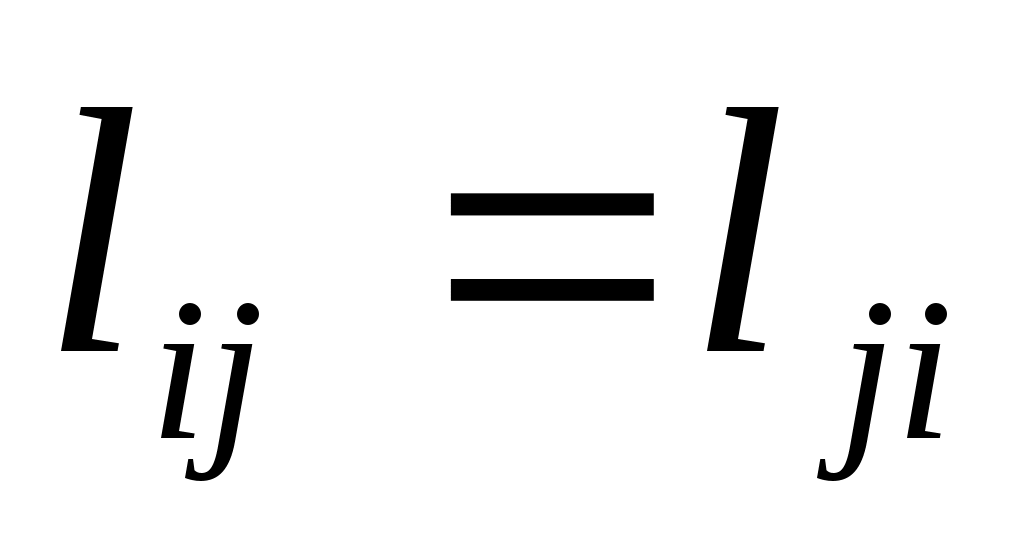 . .
Для решения задачи используем метод динамического программирования и отыскиваем кратчайшее расстояние неот фиксированной точки
до всех остальных, а от всех остальных до фиксированной через соседние
точки. Связь, через которую проходит кратчайшее расстояние, после каждого шага отмечаем стрелкой. Для удобства точки сети обозначим кружками с номерами точек.
Алгоритм решения:
Фиксируем конечную точку 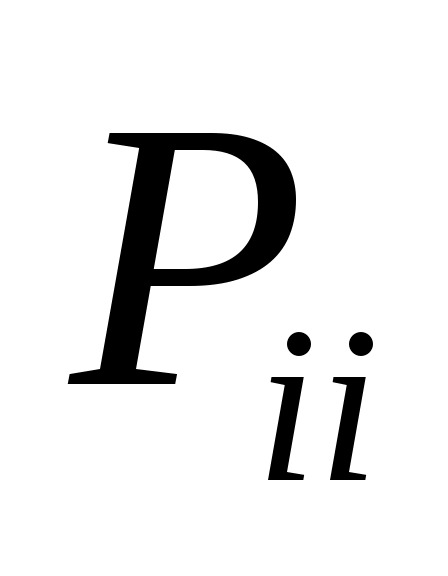 , до которой необходимо рассчитать кратчайшее расстояние от всех остальных, и рядом с этой точкой записываем нуль, т.к. расстояние , до которой необходимо рассчитать кратчайшее расстояние от всех остальных, и рядом с этой точкой записываем нуль, т.к. расстояние 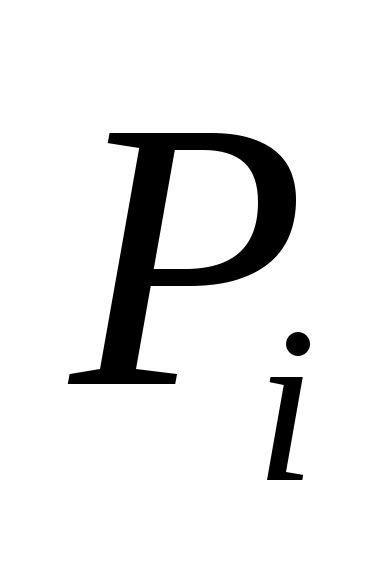 от точки до ней самой равно 0.Это число, отличное от нуля, для других точек, назовём характеристикой точки. от точки до ней самой равно 0.Это число, отличное от нуля, для других точек, назовём характеристикой точки.
Определим соседние точки по формуле 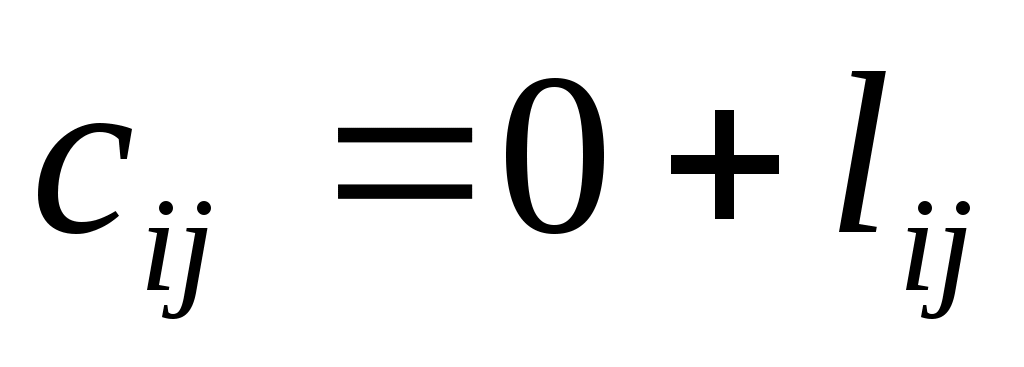 и на связях, соединяющих эти точки, поставим стрелки, направленные в точку и на связях, соединяющих эти точки, поставим стрелки, направленные в точку 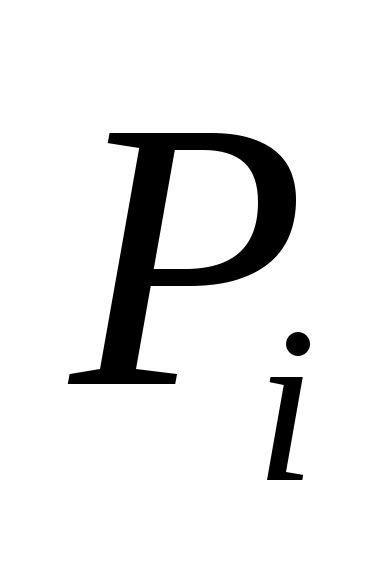 . После этого точку . После этого точку 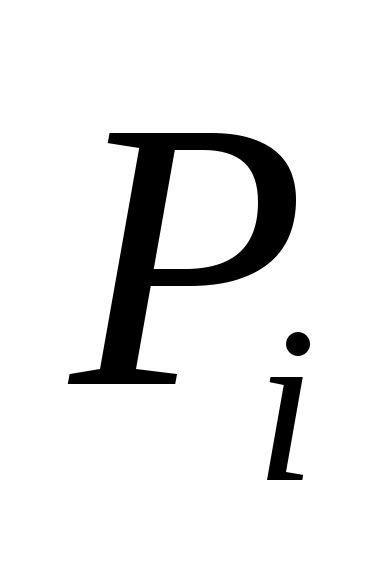 отметим символом v, обозначающим, что операции над ней закончены. отметим символом v, обозначающим, что операции над ней закончены.
Переходим к любой соседней точке, для которой характеристика уже найдена. Пусть это будет точка 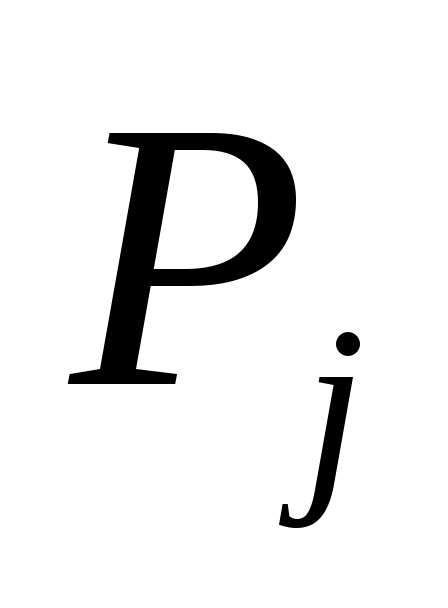 . Определяем соседние с ней точки и подсчитываем характеристики этих точек по формуле . Определяем соседние с ней точки и подсчитываем характеристики этих точек по формуле 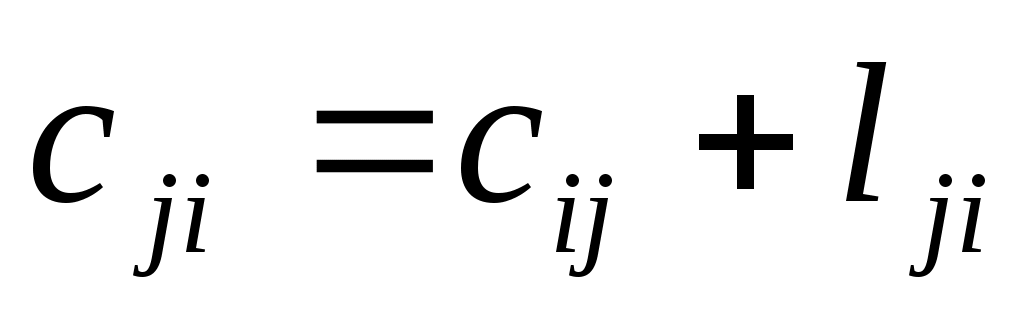 . .
При определении 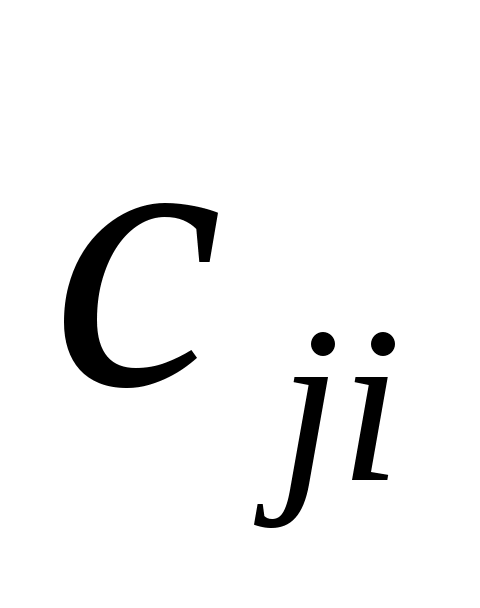 для соседних для соседних 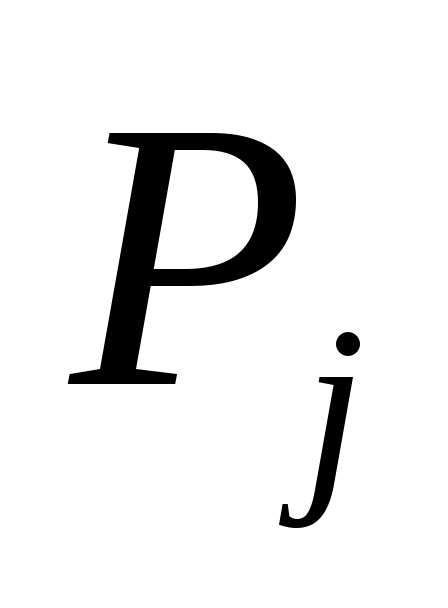 может оказаться, что для некоторых из них характеристики может оказаться, что для некоторых из них характеристики  уже известны. В этом случае новую характеристику уже известны. В этом случае новую характеристику 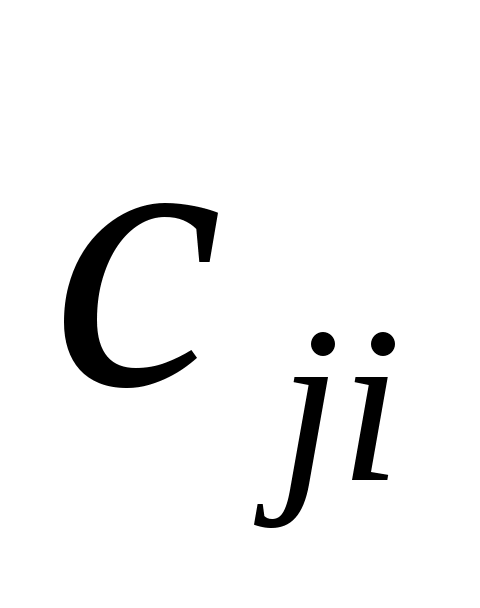 сравниваем со старой характеристикой сравниваем со старой характеристикой  . .
Если 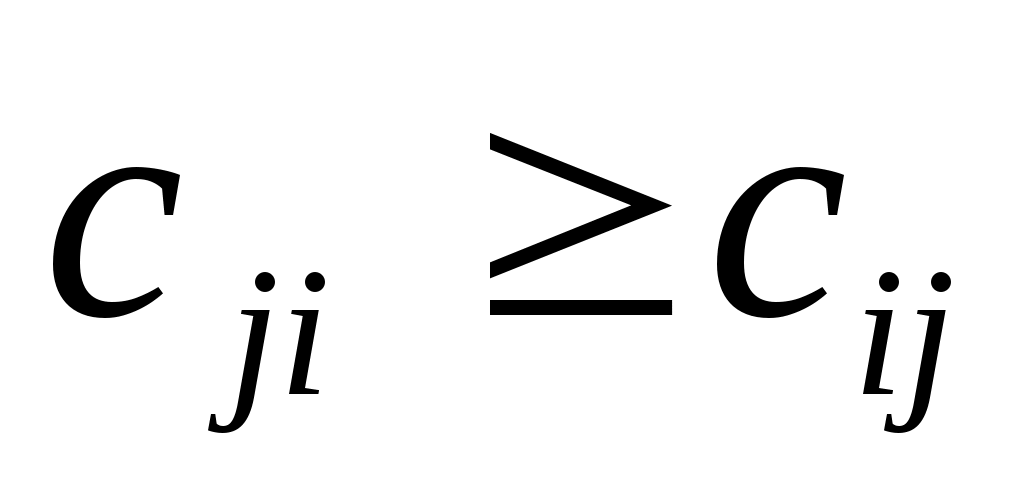 , то старую характеристику оставляем без изменений. , то старую характеристику оставляем без изменений.
Если 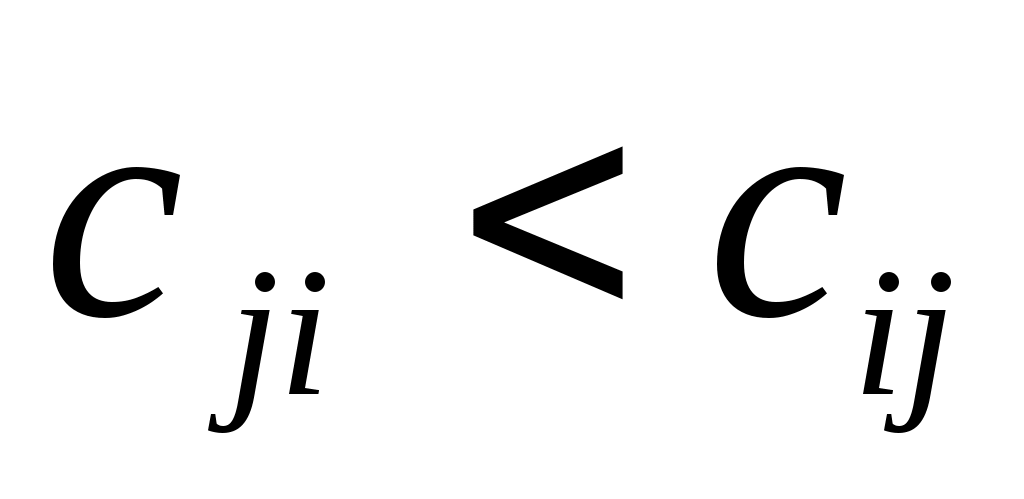 , то старую характеристику заменяем на новую, соответственно происходит или не происходит изменение направления. , то старую характеристику заменяем на новую, соответственно происходит или не происходит изменение направления.
Точку 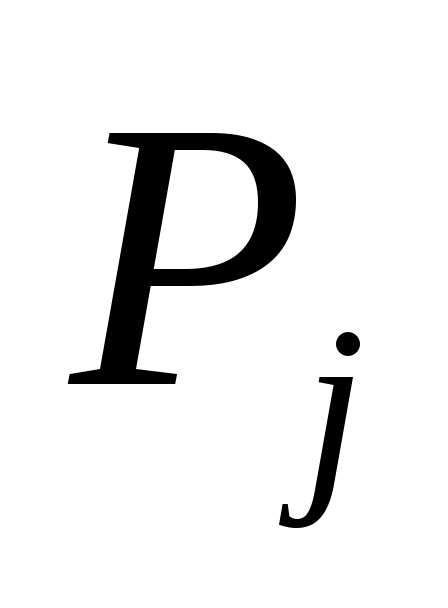 отмечаем символом v, если соседняя точка, у которой изменилась характеристика, не была ранее отмечена v. Если же точка ранее была отмечена символом v, то пересчитываем характеристики соседних с ней точек. отмечаем символом v, если соседняя точка, у которой изменилась характеристика, не была ранее отмечена v. Если же точка ранее была отмечена символом v, то пересчитываем характеристики соседних с ней точек.
Переходим к пункту 3.
Процесс продолжаем до тех пор, пока не будут отмечены символом v все точки сети. Ответ выписываем в виде таблицы, где указаны кратчайшее расстояние от всех точек до конечной и пункты, через которые они проходят.
Порядок выполнения заданий
Задача 1. Двум предприятиям А и В на 4 квартала выделено 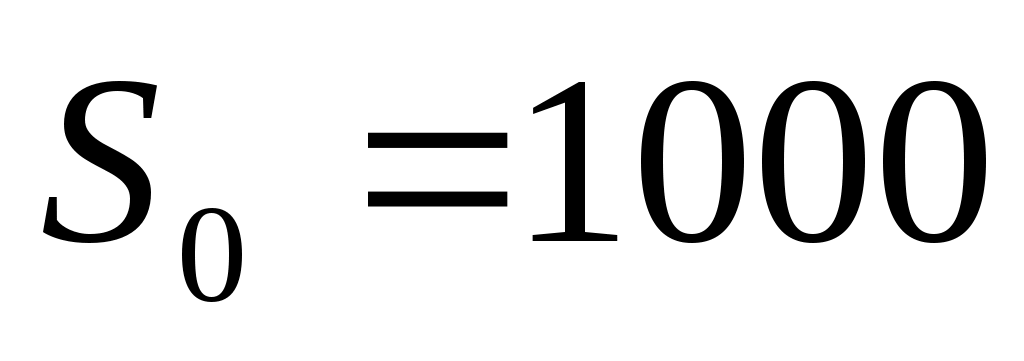 единиц средств. Каждый квартал предприятие А получает х средств, предприятие В - у средств. При этом от выделенных средств предприятие А получает 5х единиц и остаток средств 0,3х единиц, а предприятие В - доход 4у единиц и остаток выделенных средств 0,5у единиц. Необходимо распределить средства между предприятиями поквартально таким образом, чтобы за весь год оба предприятия получили максимальный доход. единиц средств. Каждый квартал предприятие А получает х средств, предприятие В - у средств. При этом от выделенных средств предприятие А получает 5х единиц и остаток средств 0,3х единиц, а предприятие В - доход 4у единиц и остаток выделенных средств 0,5у единиц. Необходимо распределить средства между предприятиями поквартально таким образом, чтобы за весь год оба предприятия получили максимальный доход.
Решение. Период времени 1 год разделим на 4 квартала (4 этапа).
Введем обозначения: через  обозначим вклад в развитие предприятий А и В в 1-ом квартале, обозначим вклад в развитие предприятий А и В в 1-ом квартале, 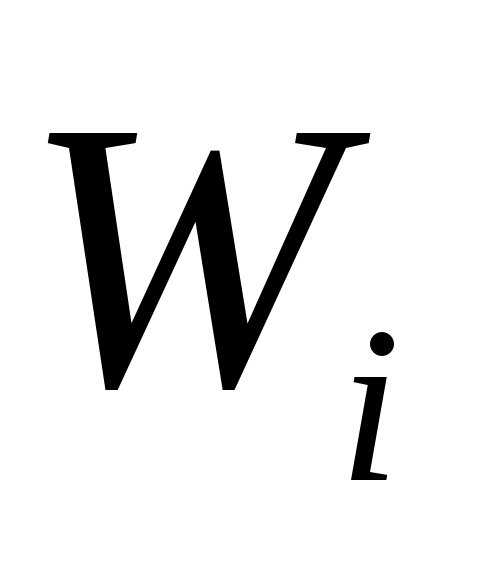 - доход за i-ый квартал, - доход за i-ый квартал, 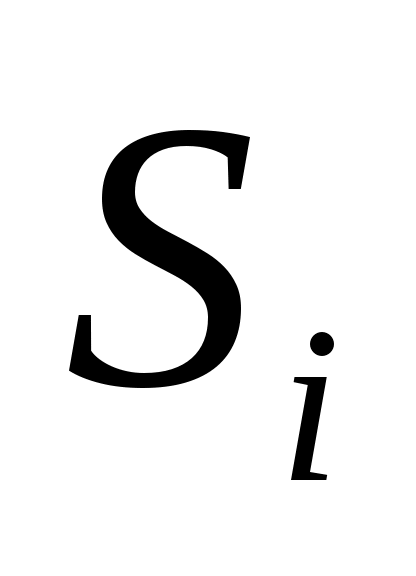 - остаток средств на конец i-ого квартала, i – 1,2,3,4. - остаток средств на конец i-ого квартала, i – 1,2,3,4.
№
|
Состояние
|
Вклад
|
Доход
|
Остаток
|
А
|
В
|
1
|
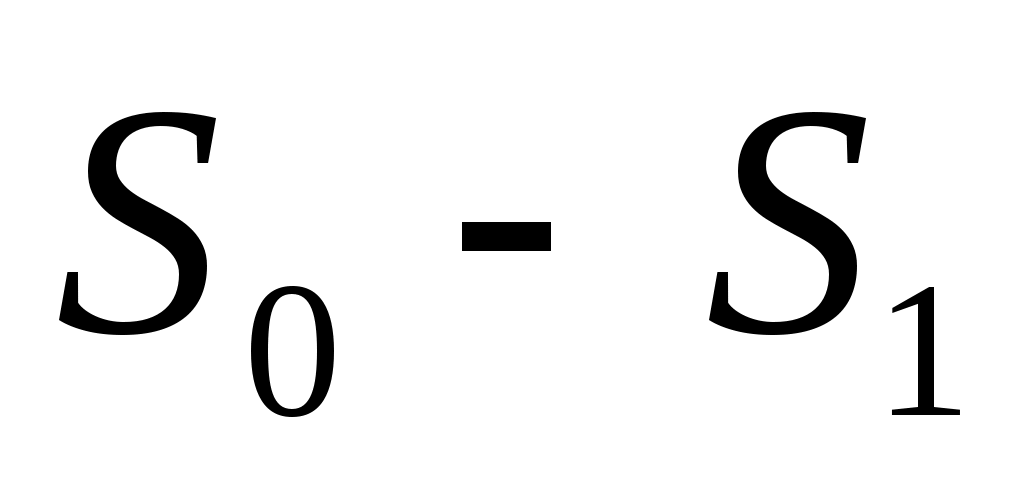
|
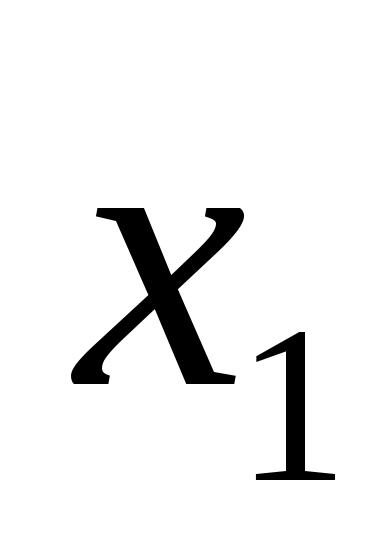
|
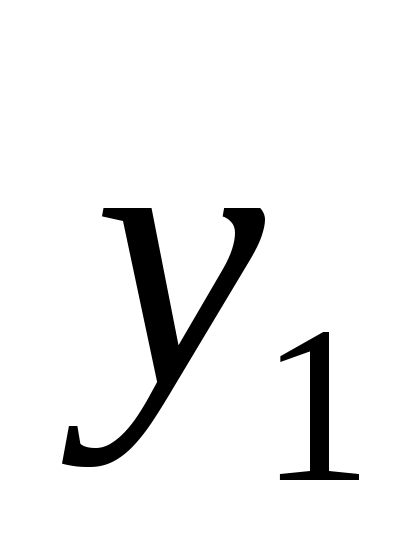
|
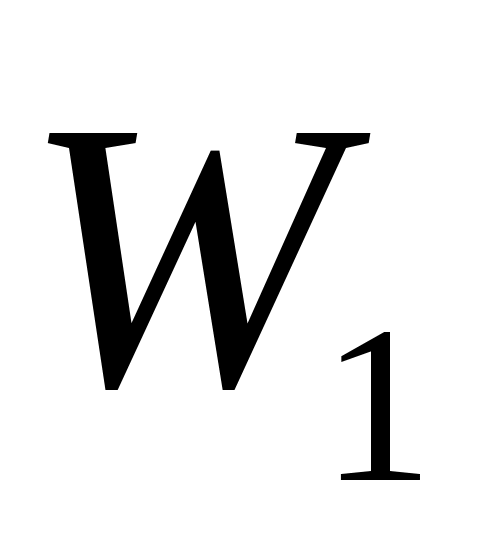
|
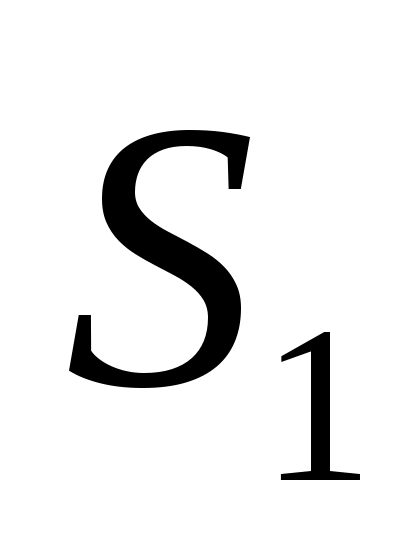
|
2
|
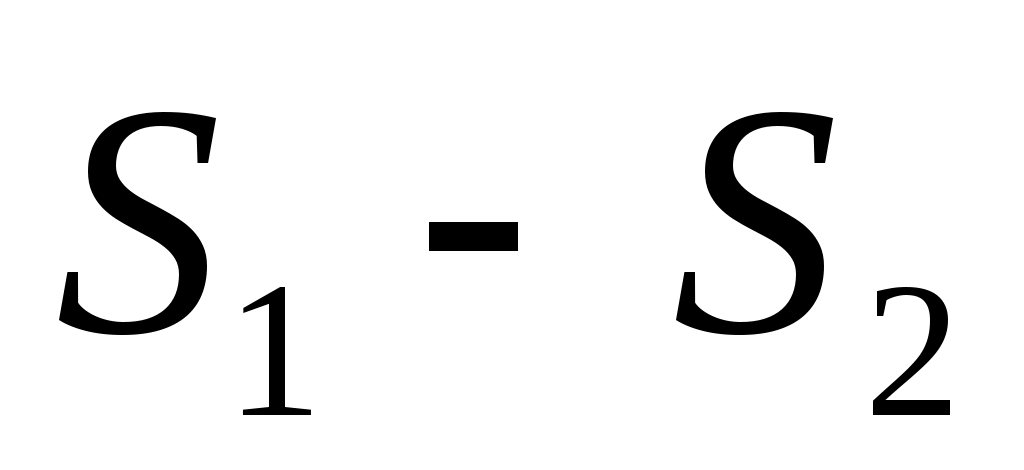
|
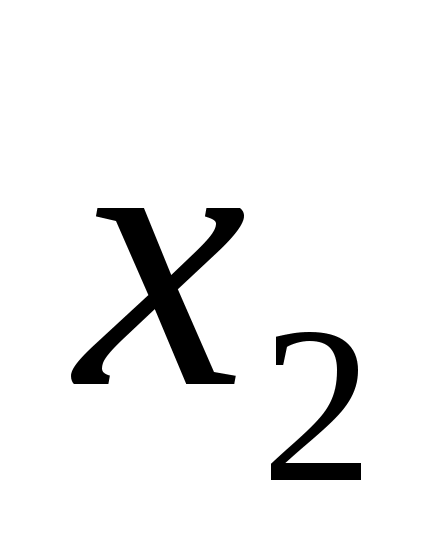
|
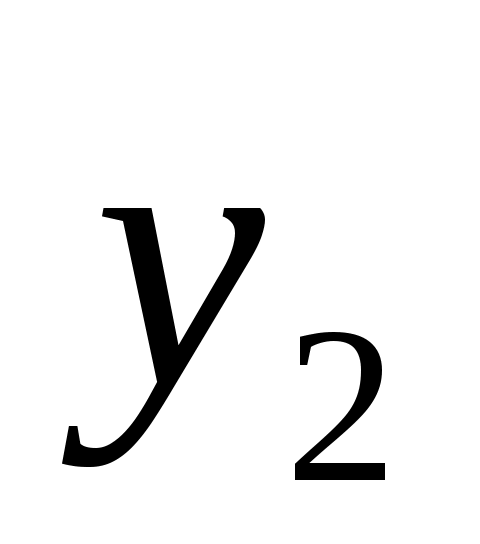
|
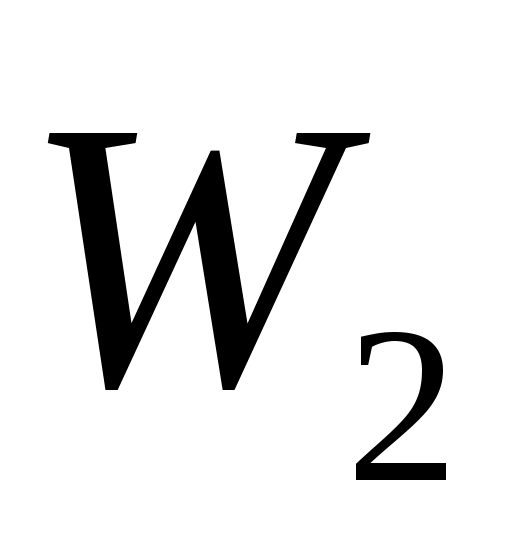
|
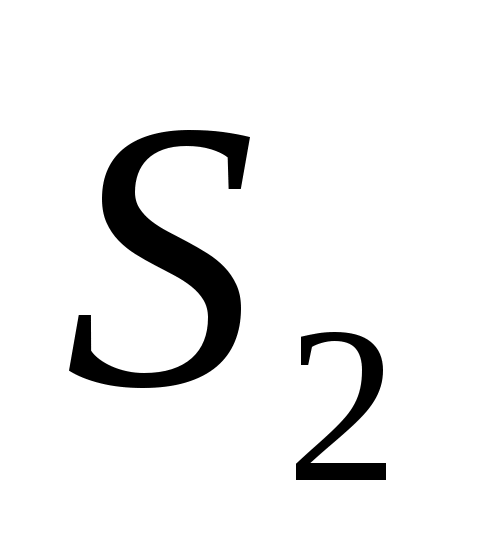
|
3
|
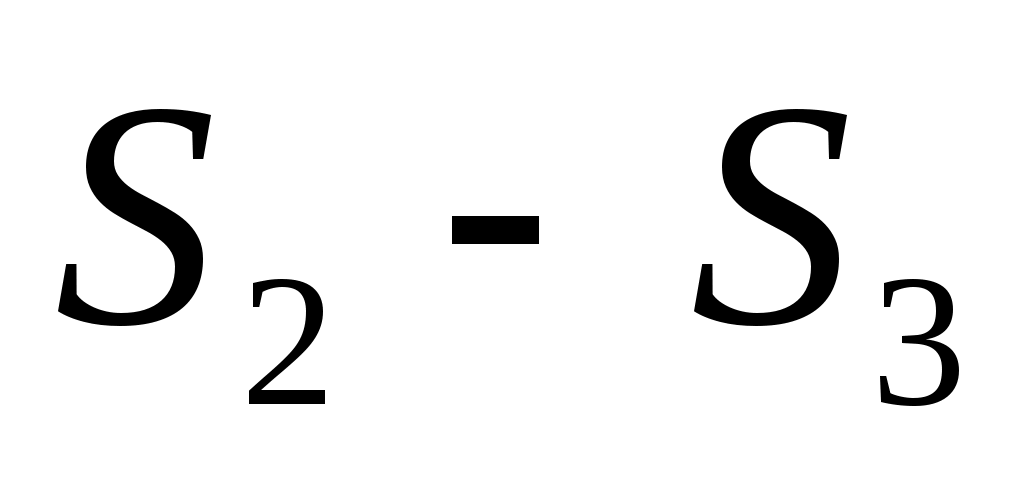
|
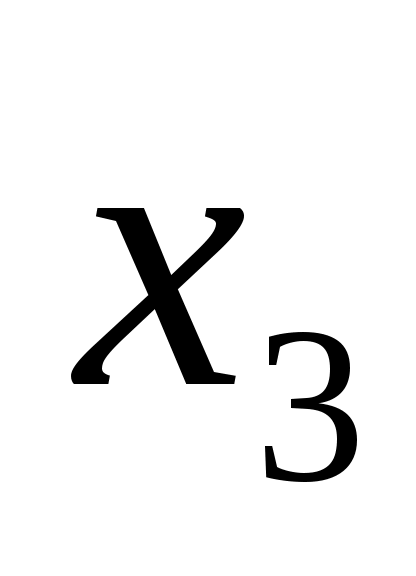
|
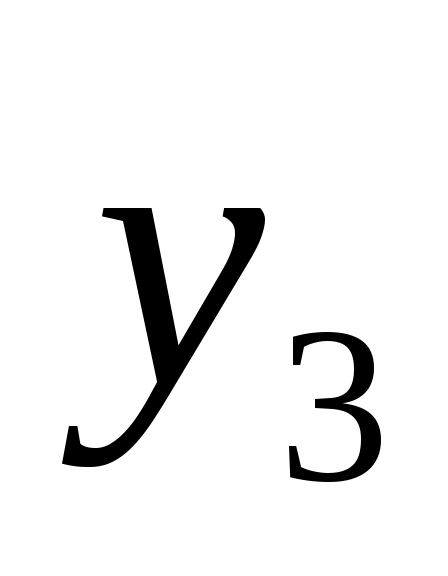
|
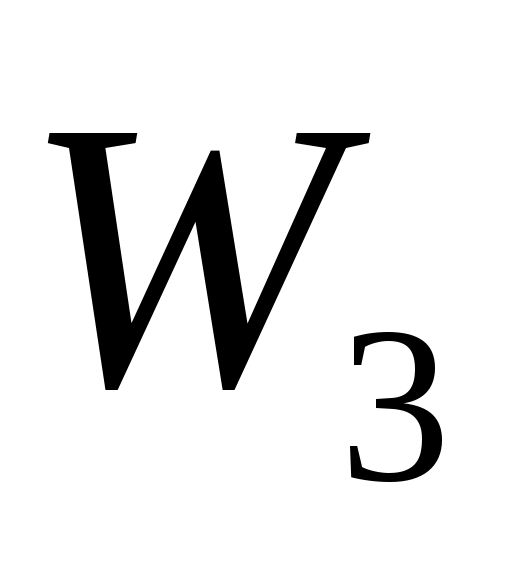
|
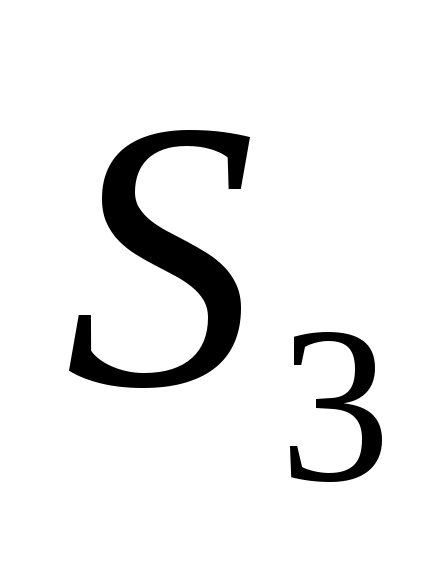
|
4
|
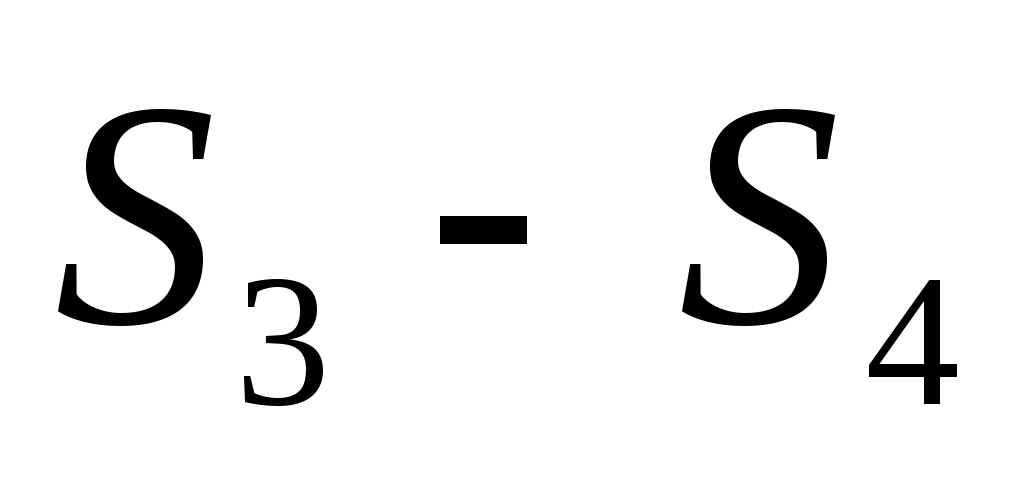
|
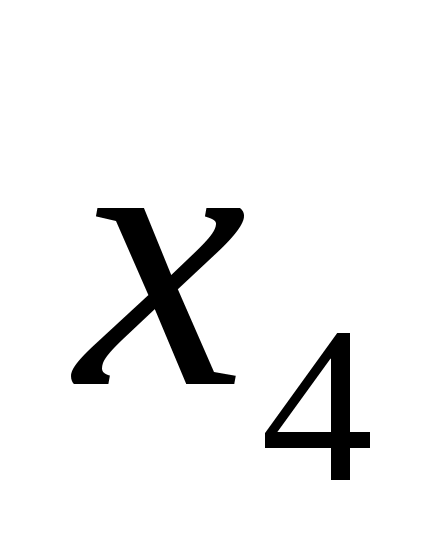
|
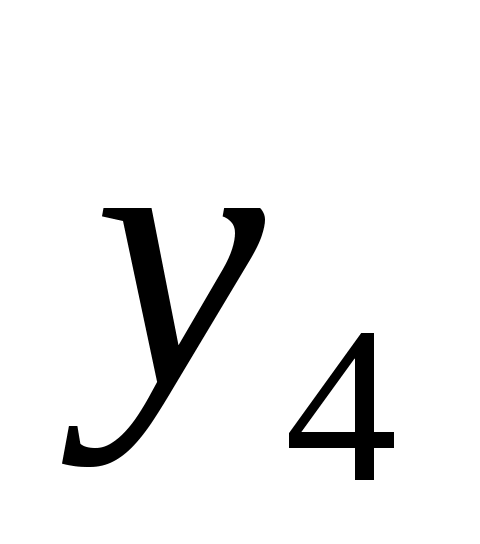
|
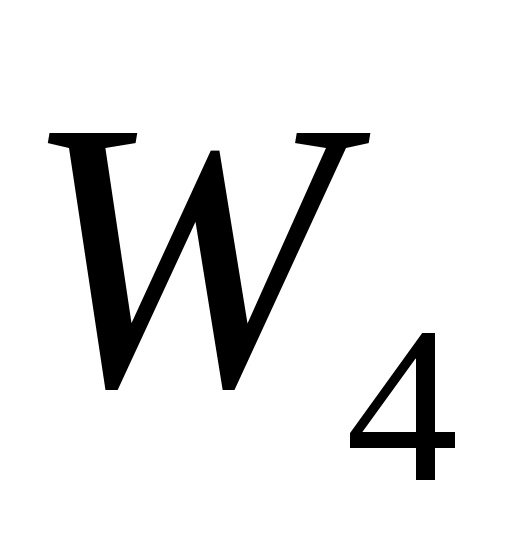
|
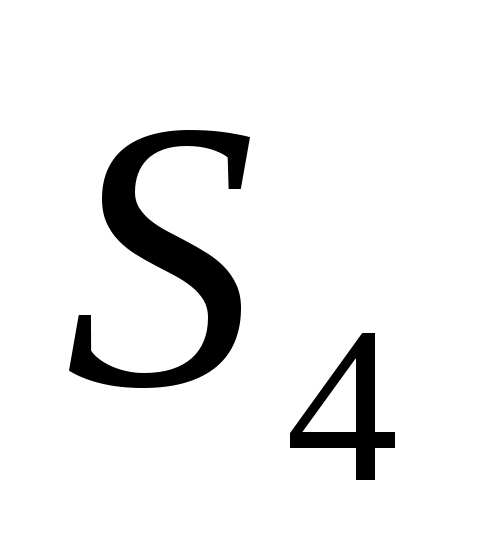
|
С учетом введенных обозначений составим подробную таблицу по этапам.
Предприятие
|
1 квартал
|
2 квартал
|
3 квартал
|
4 квартал
|
вклад
|
доход
|
остаток
|
вклад
|
доход
|
остаток
|
вклад
|
доход
|
остаток
|
вклад
|
доход
|
А
|
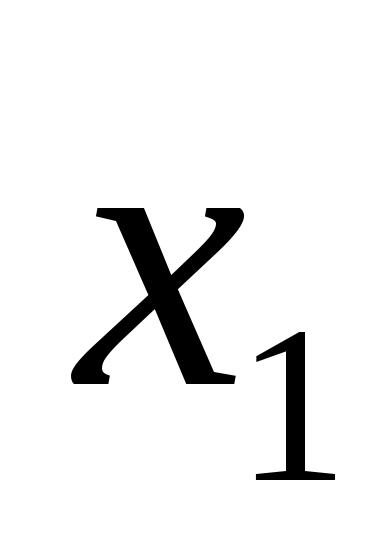
|
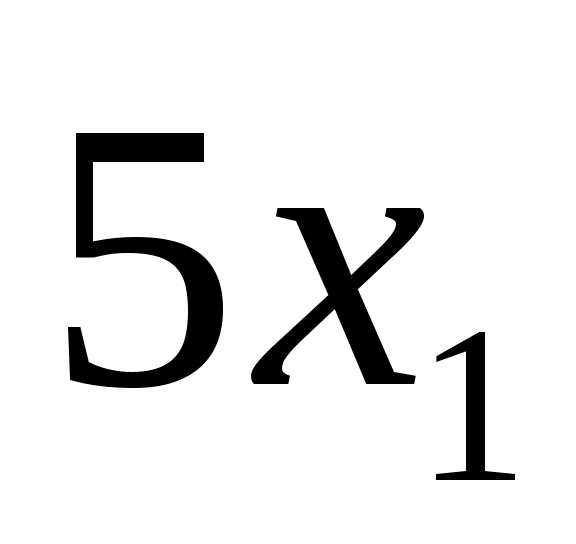
|
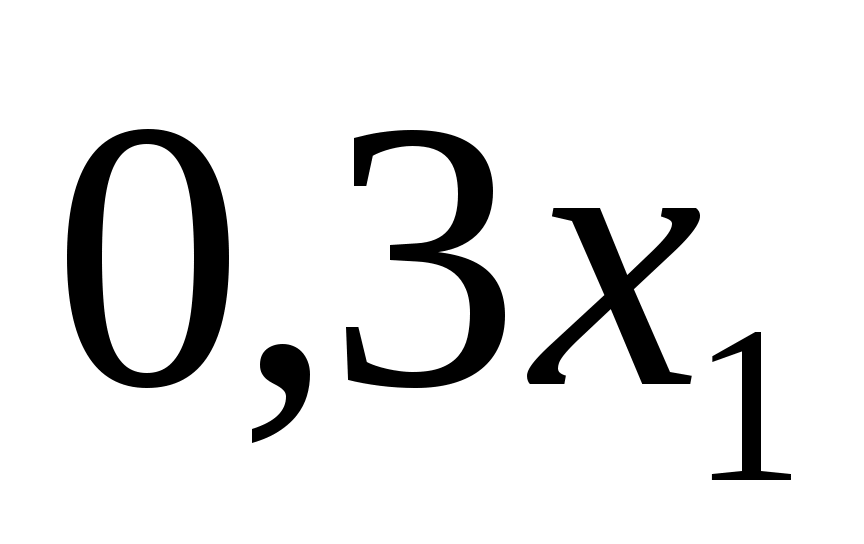
|
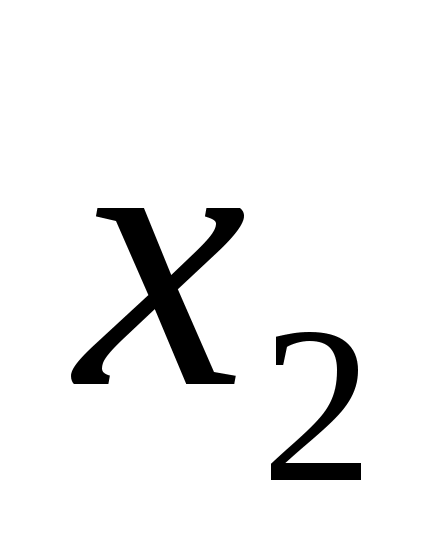
|
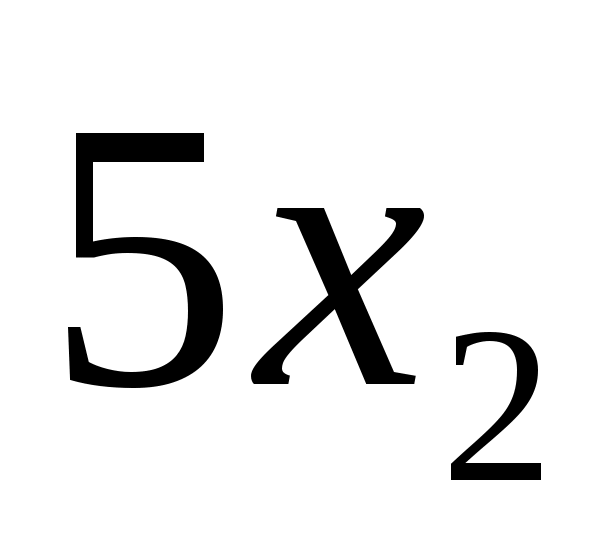
|
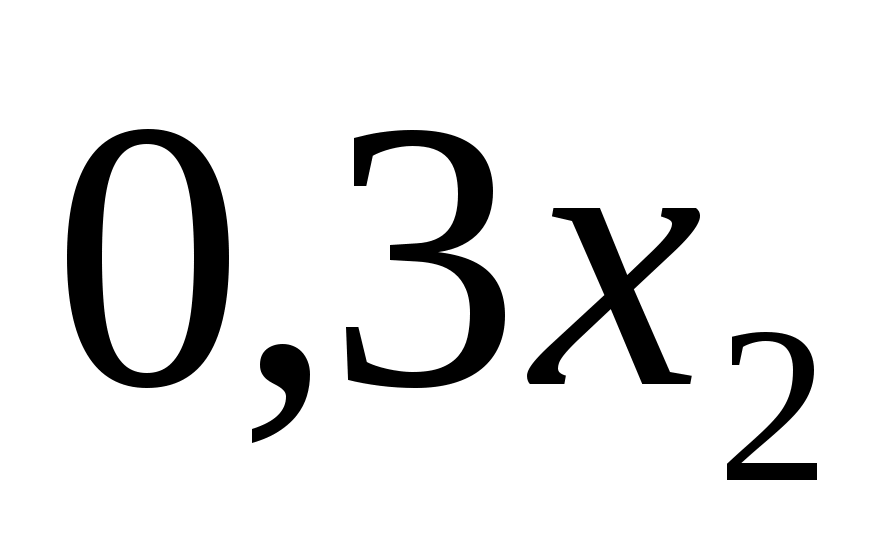
|
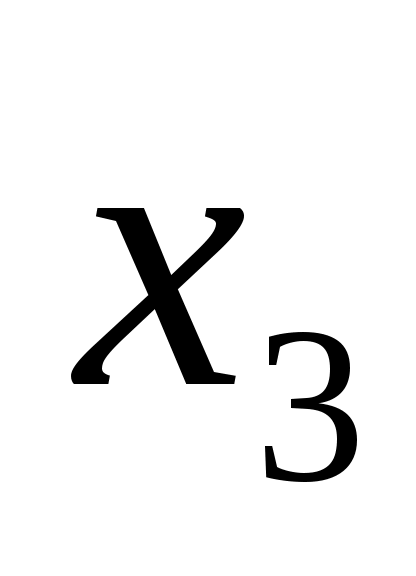
|
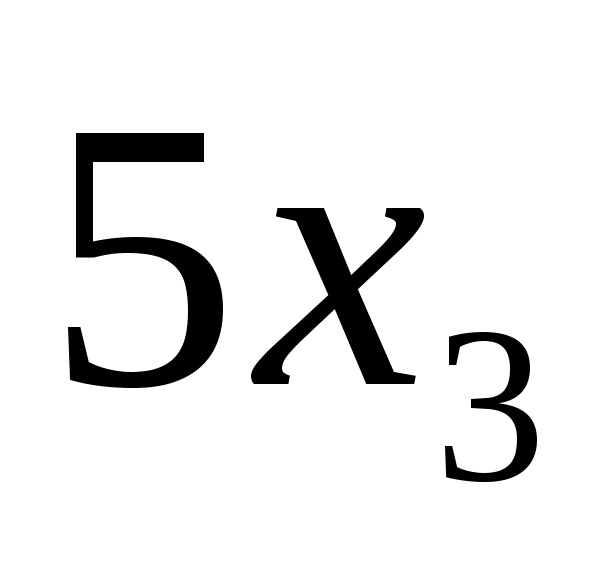
|
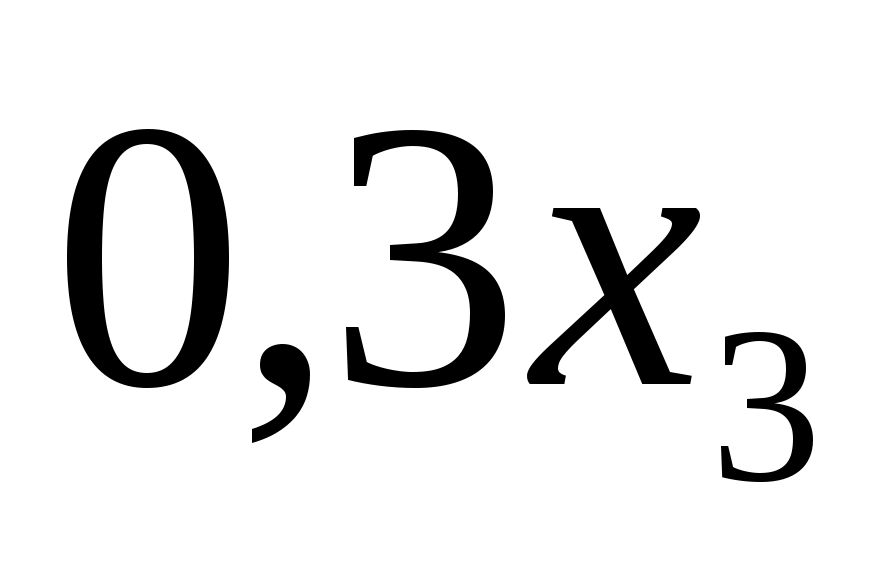
|
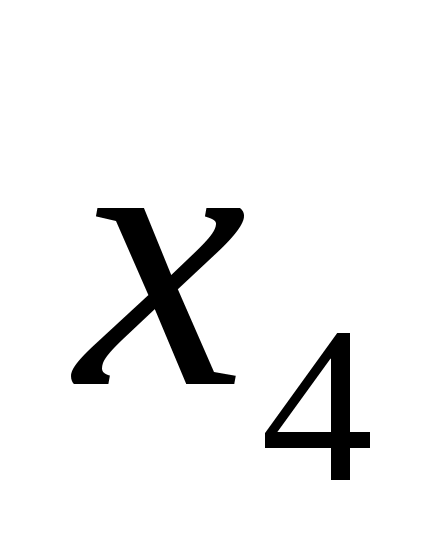
|
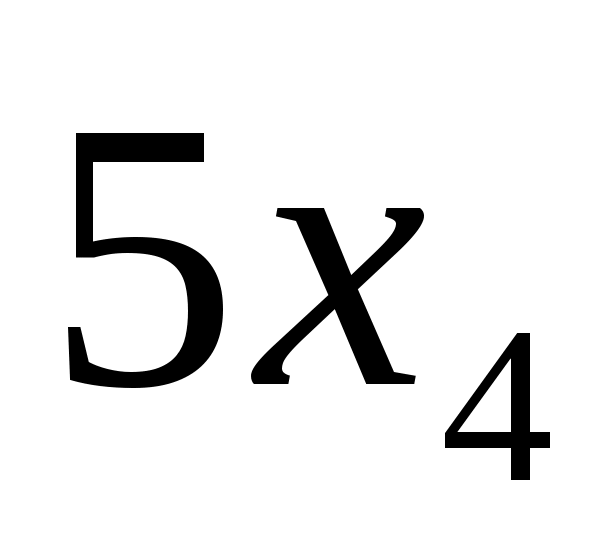
|
В
|
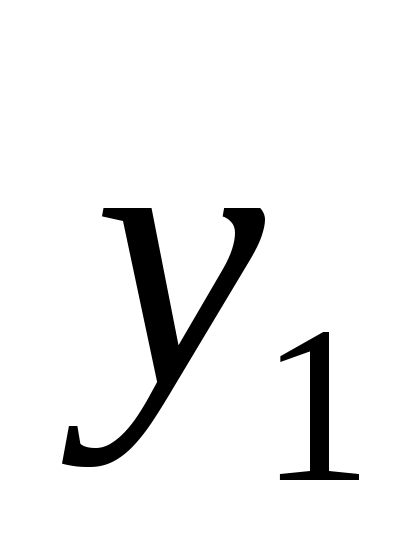
|
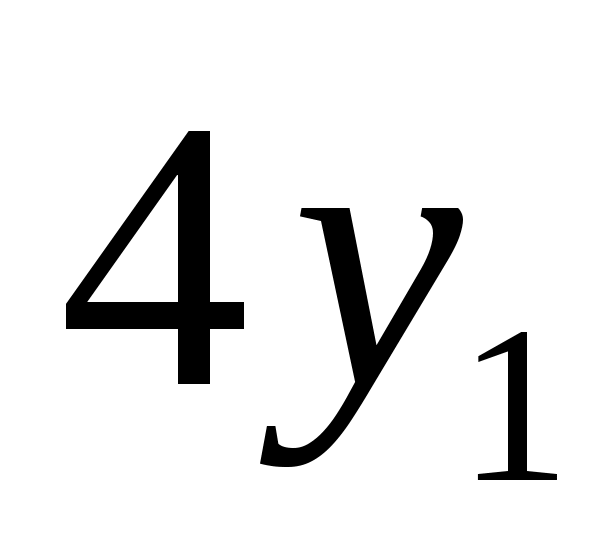
|
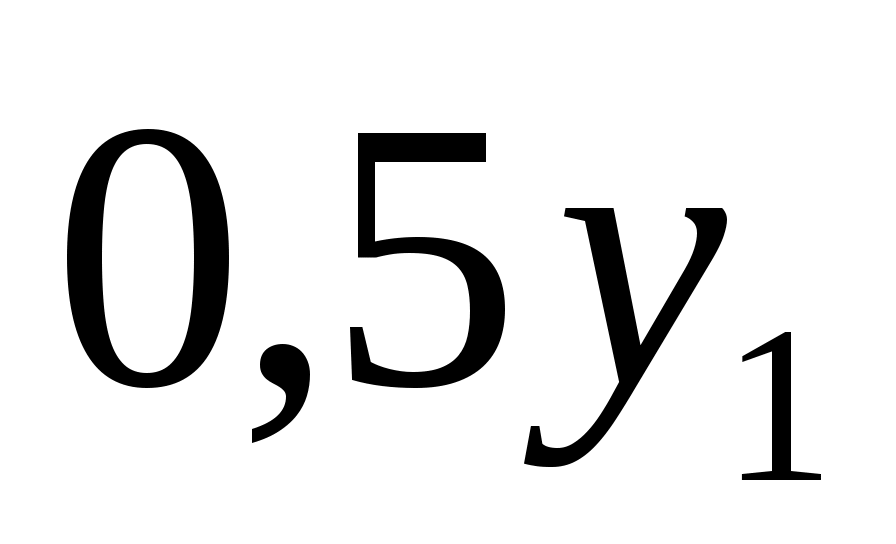
|
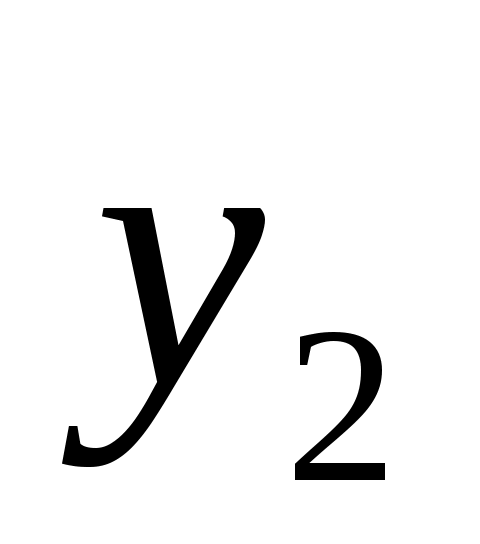
|
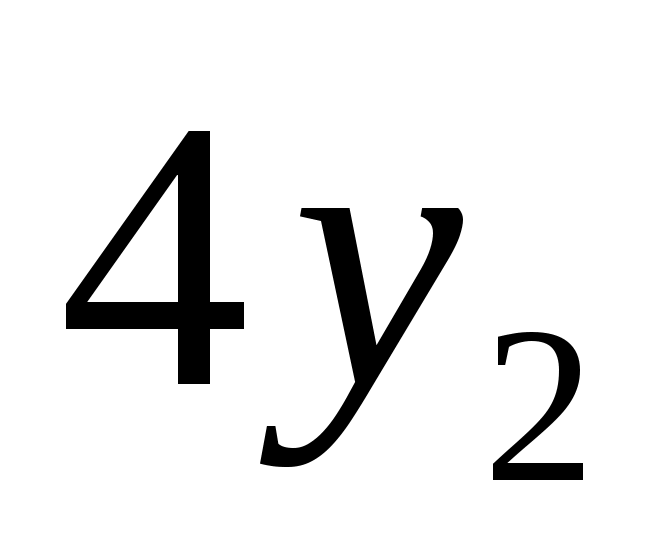
|
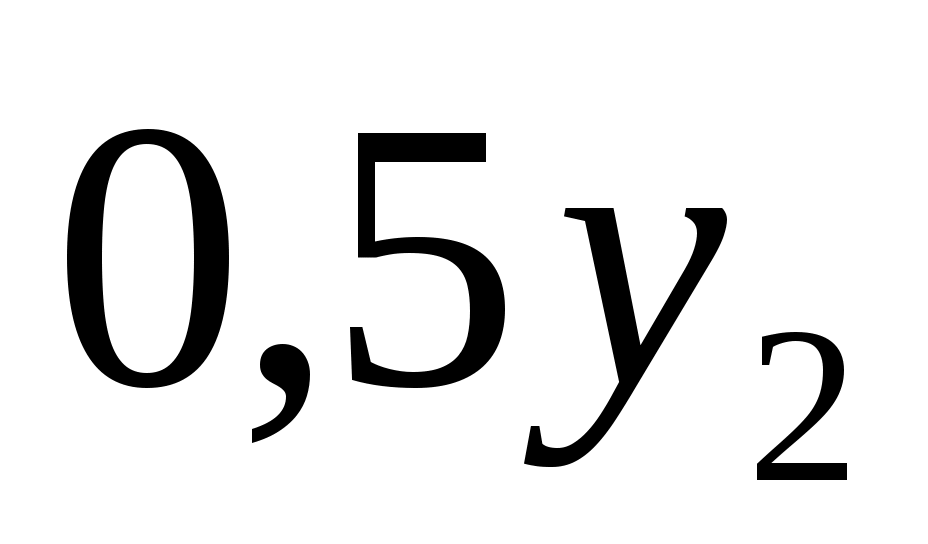
|
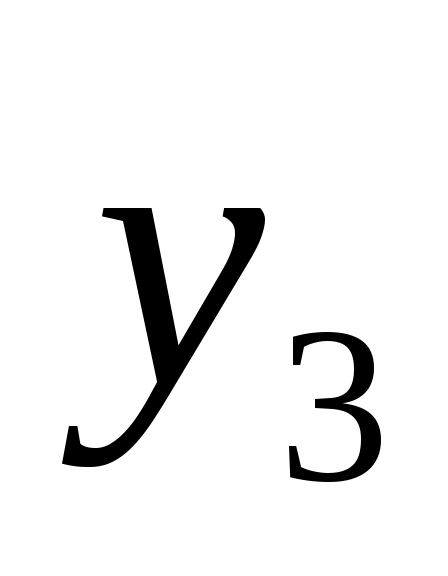
|
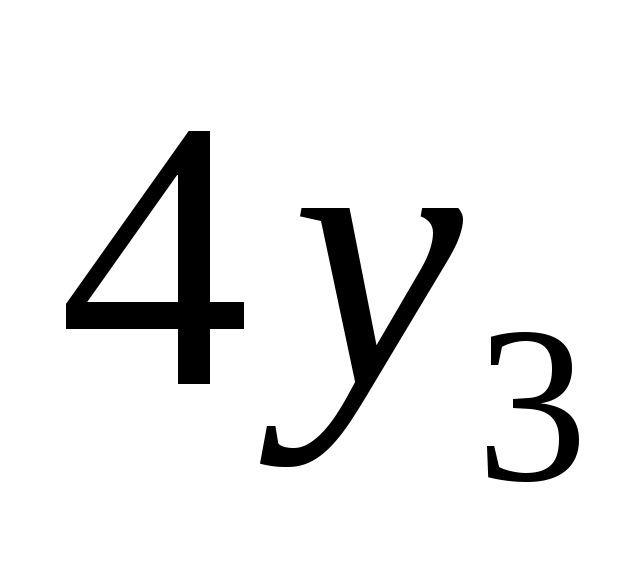
|
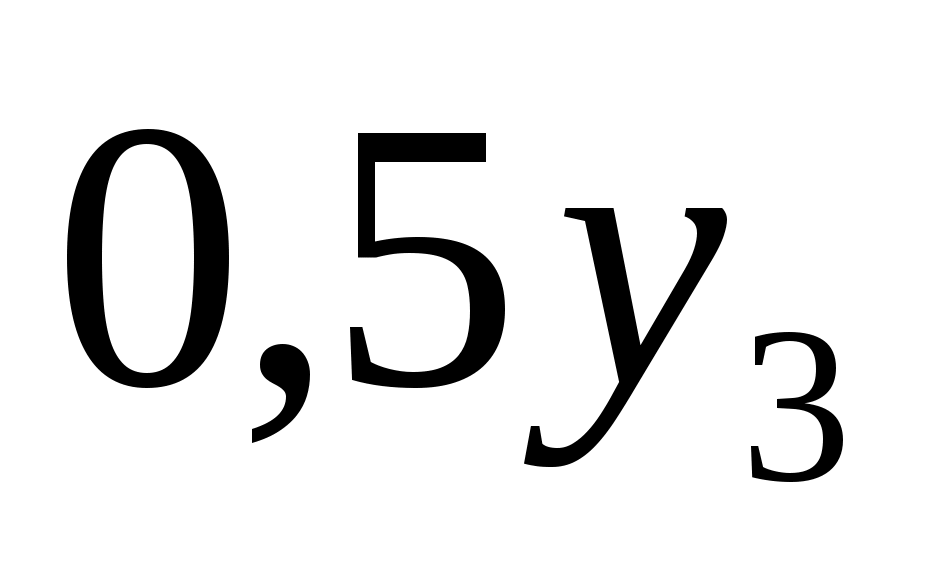
|
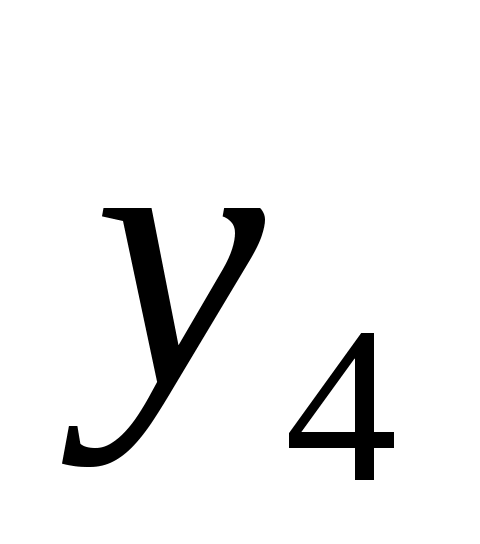
|
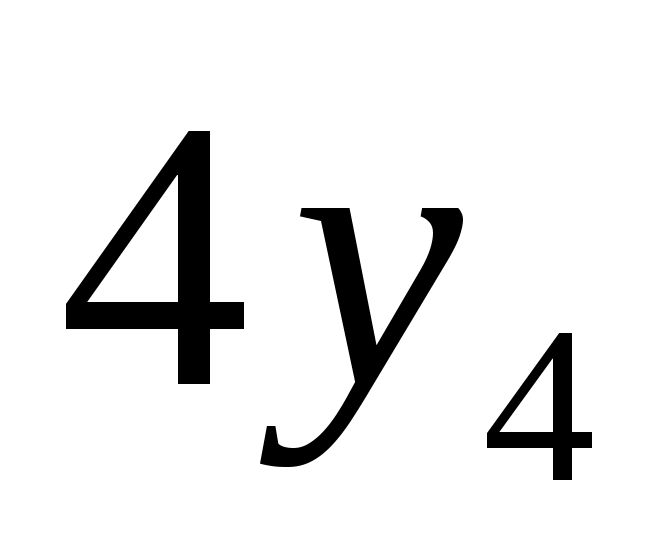
|
|
S0=x1+y1
|
W1=5x1+4y1
|
S1=0,3x1+0,5y1
|
S1=x2+y2
|
W2=5x2+4y2
|
S2=0,3x2+0,5y2
|
S2=x3+y3
|
W3=5x3+4y3
|
S3=0,3x3+0,5y3
|
S3=x4+y4
|
W4=5x4+4y4
|
Отыскание оптимального управления начнем с 4 квартала.
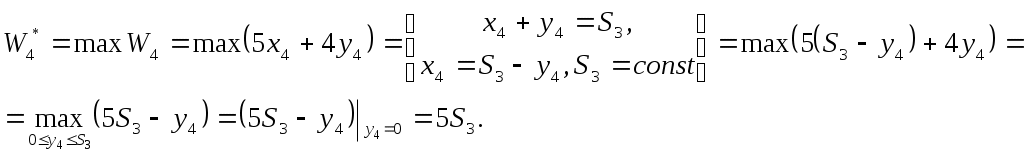
3 квартал.
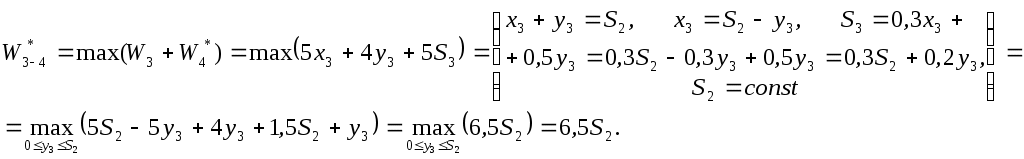 Так как максимум дохода за 3-4 кварталы постоянен при любом распределении средств, то пусть Так как максимум дохода за 3-4 кварталы постоянен при любом распределении средств, то пусть 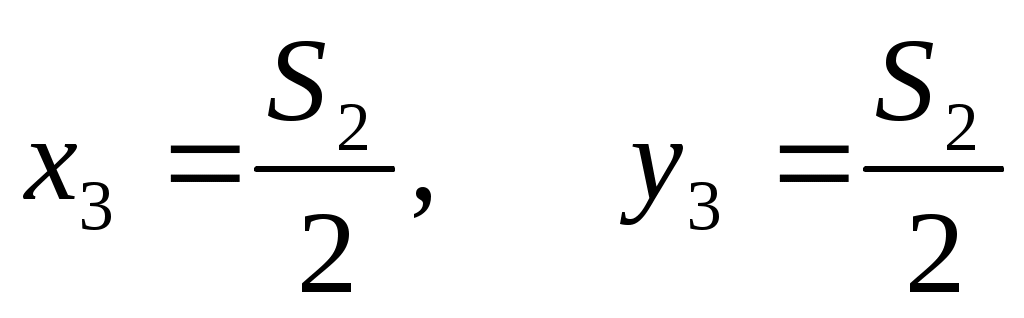 . .
2 квартал.
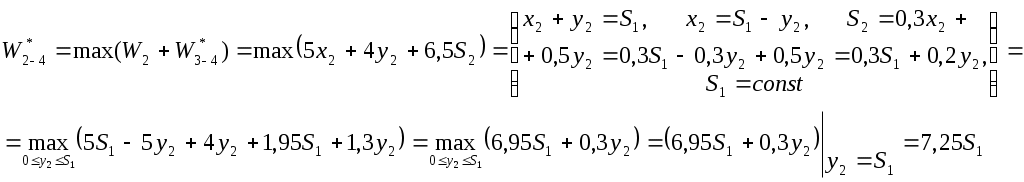
1 квартал.
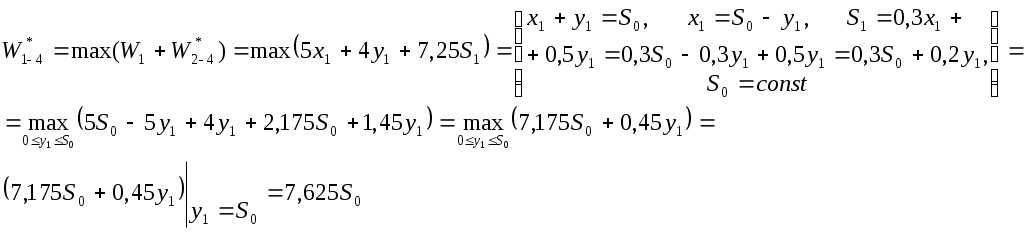
По условию задачи 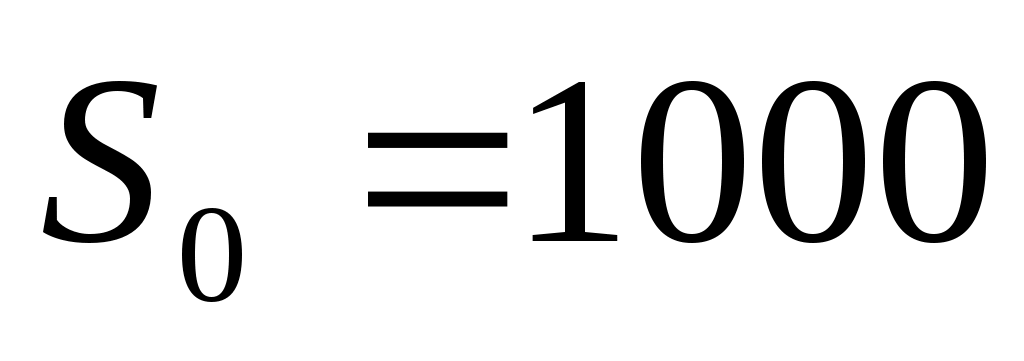 единиц, единиц, 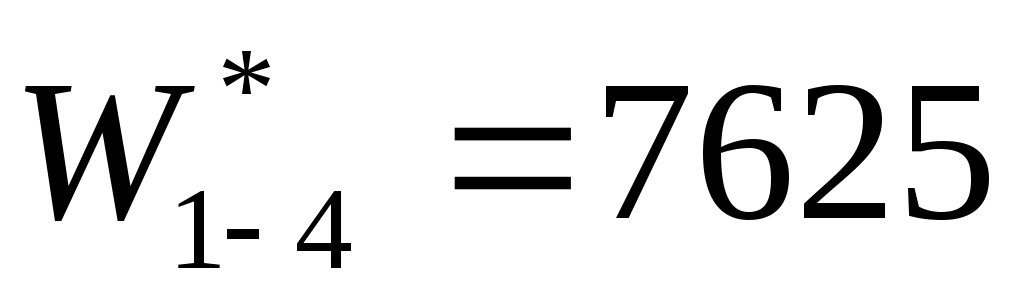 единиц, при этом будем иметь следующие распределение средств по кварталам: единиц, при этом будем иметь следующие распределение средств по кварталам:
Квартал
|
Распределяемые средства
|
Вклады
|
А
|
В
|
1
|
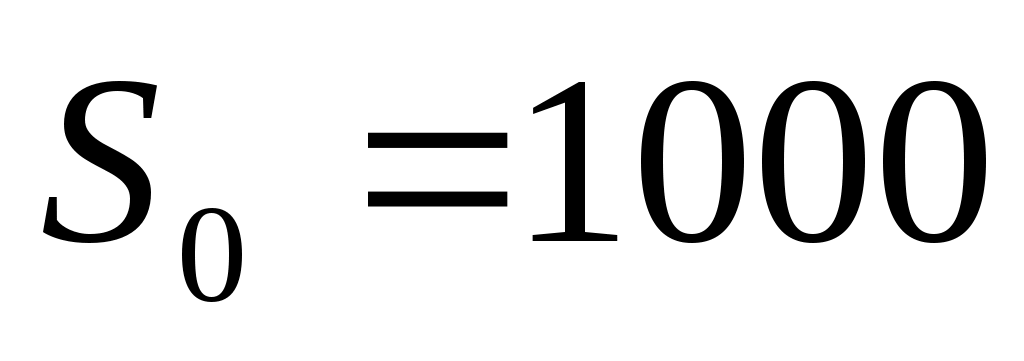
|
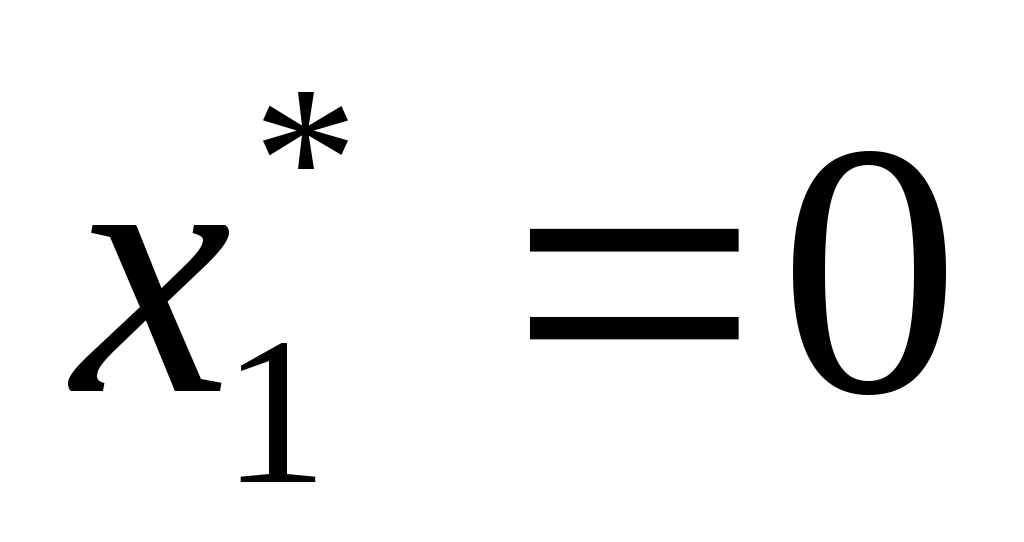
|
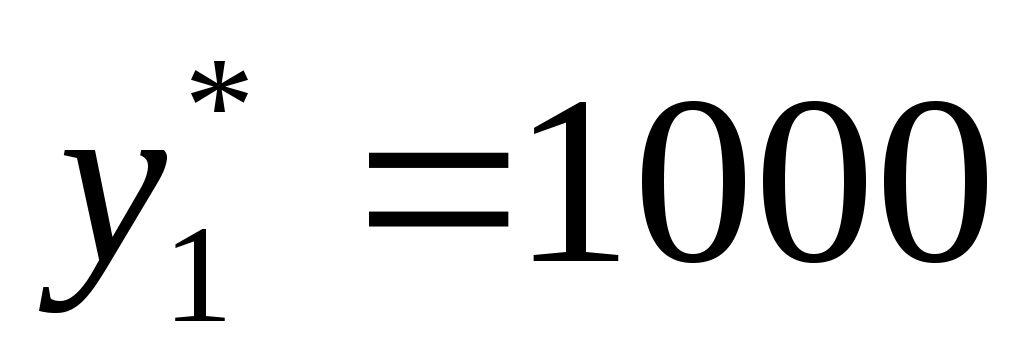
|
2
|
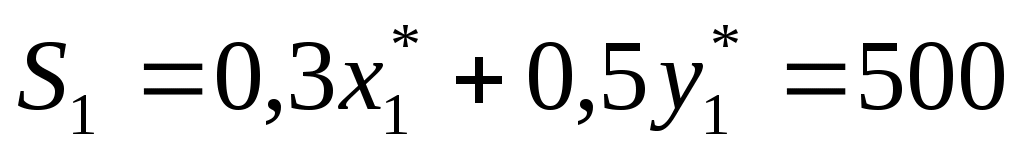
|
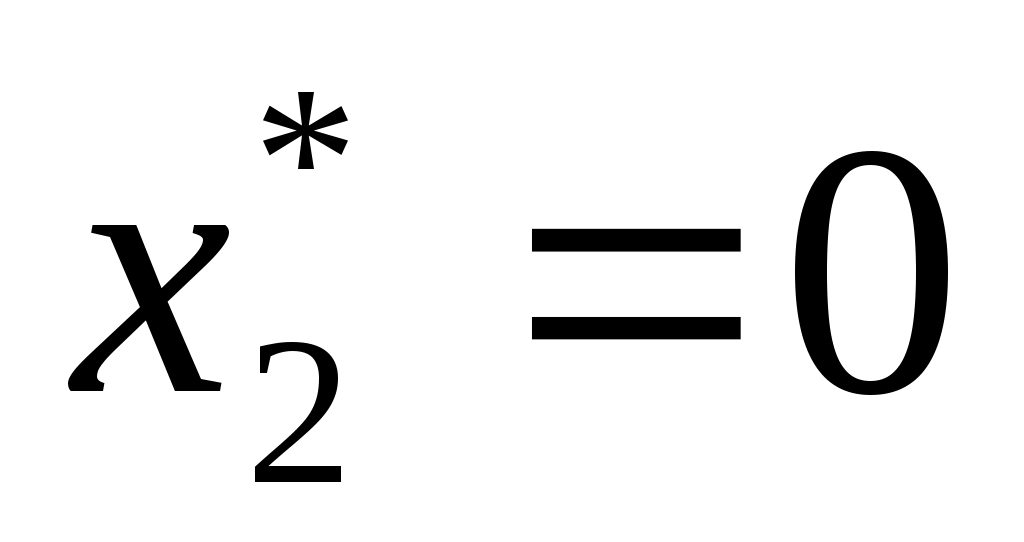
|
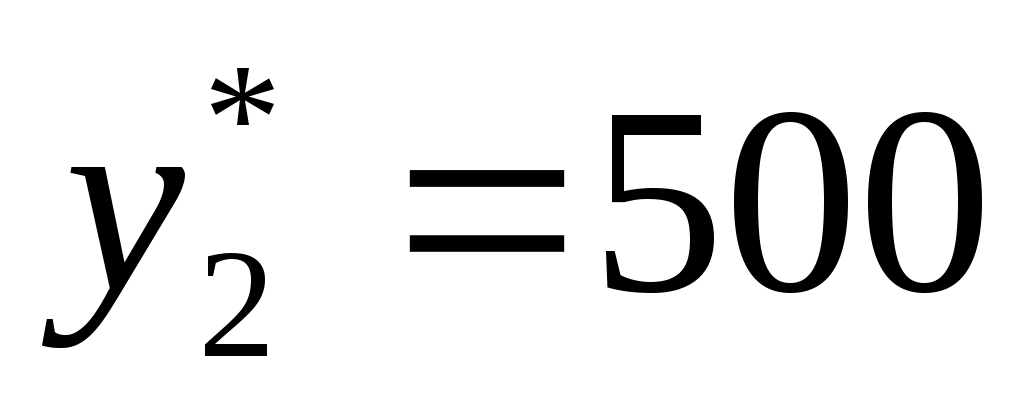
|
3
|
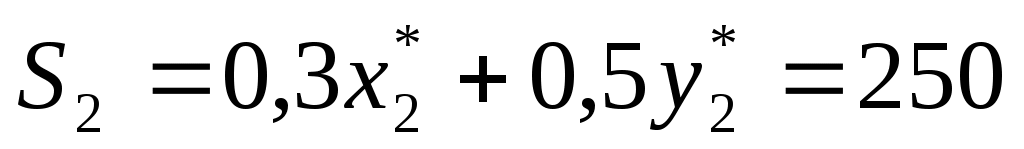
|
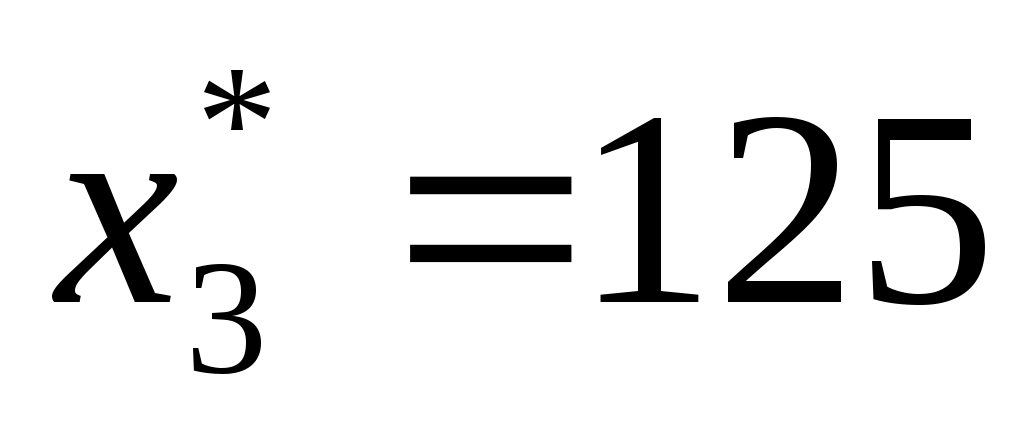
|
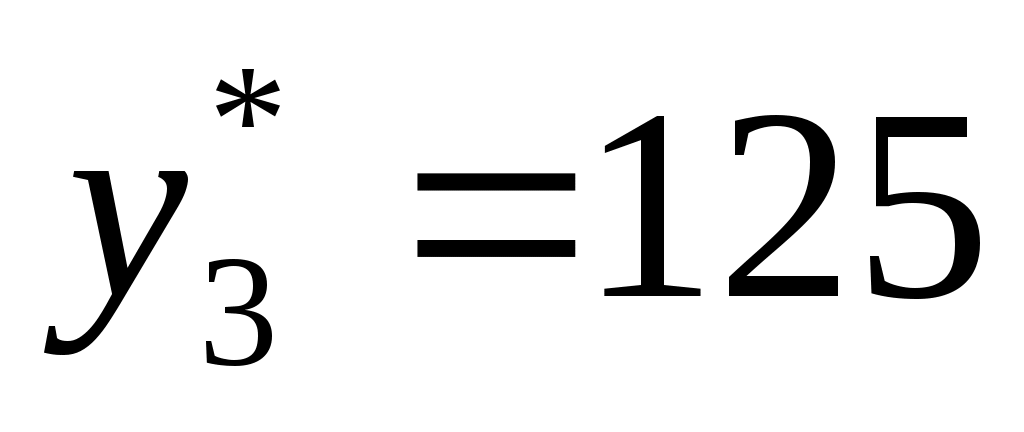
|
4
|
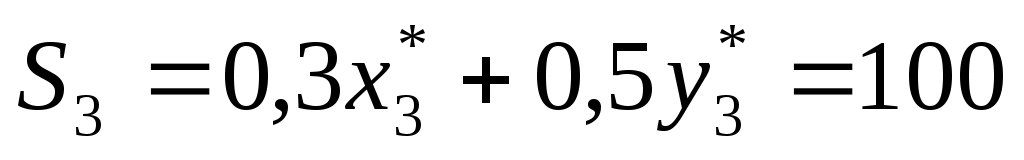
|
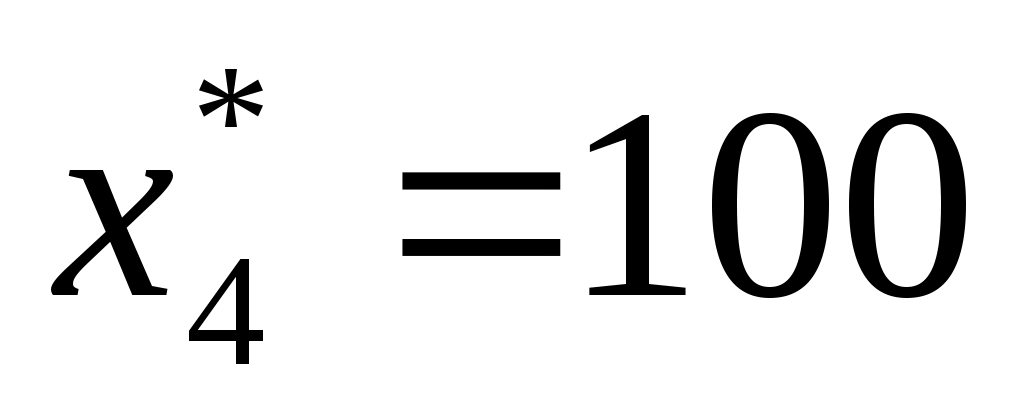
|
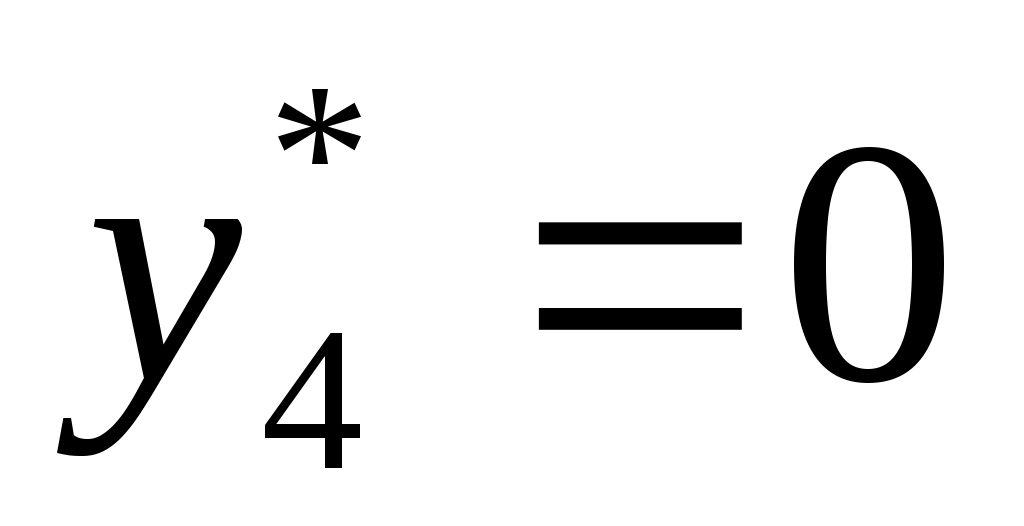
|
|
|
|
 Скачать 1.97 Mb.
Скачать 1.97 Mb.
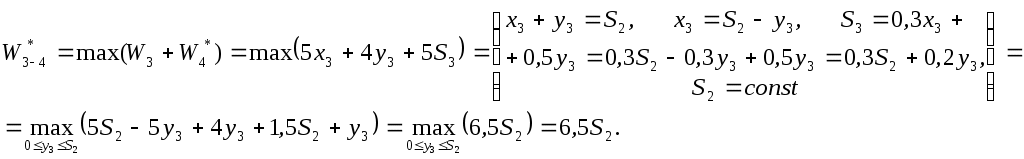 Так как максимум дохода за 3-4 кварталы постоянен при любом распределении средств, то пусть
Так как максимум дохода за 3-4 кварталы постоянен при любом распределении средств, то пусть