ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb.
|
|
Задача 2. Дана сеть, состоящая из 7 точек, и известны расстояния между точками. Необходимо определить кратчайшее расстояние от любой точки до точки 7. Решение. 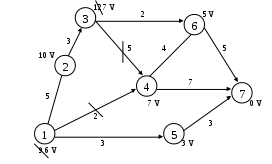 Рассмотрим точку 7.Рядом с кружком ставим 0 характеристику этой точки. Соседними с точкой 7 являются точки 6,5,4. Подсчитаем характеристики этих точек и укажем направления. Точку 7 отмечаем символом V , т.к. операции на ней закончены. Рассмотрим точку 4. Соседними с ней будут точки 6,3,1,7, Находим характеристики каждой из них. Характеристики точек 1 и 3 – соответственно 9 и 12. Характеристики точек 6,7 остались без изменения, так как 7+4=11>5, 7+7=14>0. Точку 4 отметим символом V. Рассмотрим точку 6. Соседними являются точки 3,4,7. Для точки 3 новая характеристика 5+2=7>12, поэтому изменяем старую характеристику 12 на 7, и указываем новое направление. Для точек 4,7 старые характеристики остаются без изменений, т.к. 5+4=9>7, 5+5=10>0. Точку 6 отмечаем знаком V. Рассмотрим точку 5. Соседняя с ней точка 1. Новая характеристика 3+3=6<9, поэтому изменяем характеристику и направление. Точку 5 отмечаем символом V. Точка 1, характеристика которой изменилась, является соседней с точкой 4. Точка 4 отмечена символом V, поэтому пересчитываем характеристику этой точки и проверяем соседние с ней: 7+5=12>7; 7+4=11>5; 7+7=14>0. Характеристики точек 3,6,7 остаются без изменений. Рассмотрим точку 3. Соседними являются точки 2,4,6. Характеристика 2: 7+3=10, записываем эту характеристику и указываем направление. Характеристики 6,4 остались без изменения. Точку 3 отмечаем символом V. Рассмотрим точку 2. Соседними являются точки 1 и 3. Характеристики точек не изменяются, т.к. 10+5=15>б, 10+3=13>7. Точку 2 отмечаем символом V. Рассмотрим точку 1. Соседними являются точки 2,4,5. Характеристики точек не изменились, т.к. 6+5=11>10, 6+2=8>4, 6+3=9>3. Операции над всеми точками закончены. Ответ запишем в виде таблицы.
Задания для самостоятельной работы 1 вариант. Задача 1. Планируется работа двух отраслей производства А и В на 4 года. Количество х средств, вложенных в отрасль А, позволяет получить доход 2х и уменьшается до 0,6х. Количество у средств, вложенных в отрасль В, позволяет получить доход 3у и уменьшается до 0,2у. Необходимо распределить выделенные ресурсы в количестве  единиц между отраслями по годам планируемого периода для получения максимальной прибыли за весь период.Задача 2. По заданной схеме, соединяющей 10 точек, найти кратчайшее расстояние от 1 точки до 10. 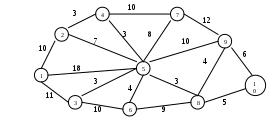 2 вариант. Задача 1. Двум предприятиям А и В на 4 квартала выделено  единиц средств. Каждый квартал предприятие А получает х средств, предприятие В - у средств. При этом от выделенных средств предприятие А получает 4х единиц и остаток средств 0,3х единиц, а предприятие В - доход 5у единиц и остаток выделенных средств 0,1у единиц. Необходимо распределить средства между предприятиями поквартально таким образом, чтобы за весь год оба предприятия получили максимальный доход. Задача 2. По заданной схеме, соединяющей 10 точек, найти кратчайшее расстояние от 1 точки до 10. 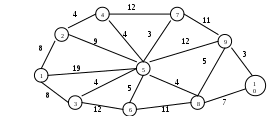 3 вариант. Задача 1. Планируется работа двух отраслей производства А и В на 4 года. Количество х средств, вложенных в отрасль А, позволяет получить доход 5х и уменьшается до 0,1х. Количество у средств, вложенных в отрасль В, позволяет получить доход 3у и уменьшается до 0,5у. Необходимо распределить выделенные ресурсы в количестве  единиц между отраслями по годам планируемого периода для получения максимальной прибыли за весь период.Задача 2. По заданной схеме, соединяющей 10 точек, найти кратчайшее расстояние от 1 точки до 10. 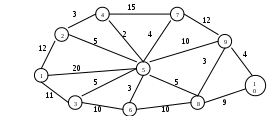 4 вариант. Задача 1. Двум предприятиям А и В на 4 квартала выделено  единиц средств. Каждый квартал предприятие А получает х средств, предприятие В - у средств. При этом от выделенных средств предприятие А получает 4х единиц и остаток средств 0,3х единиц, а предприятие В - доход 3у единиц и остаток выделенных средств 0,6у единиц. Необходимо распределить средства между предприятиями поквартально таким образом, чтобы за весь год оба предприятия получили максимальный доход. Задача 2. По заданной схеме, соединяющей 10 точек, найти кратчайшее расстояние от 1 точки до 10. 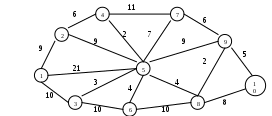 5 вариант. Задача 1. Планируется работа двух отраслей производства А и В на 4 года. Количество х средств, вложенных в отрасль А, позволяет получить доход 5х и уменьшается до 0,3х. Количество у средств, вложенных в отрасль В, позволяет получить доход 6у и уменьшается до 0,1у. Необходимо распределить выделенные ресурсы в количестве  единиц между отраслями по годам планируемого периода для получения максимальной прибыли за весь период.Задача 2. По заданной схеме, соединяющей 10 точек, найти кратчайшее расстояние от 1 точки до 10. 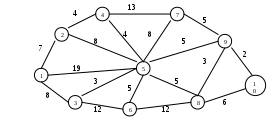 Контрольные вопросы Что называется динамическим программированием? Какие характерные особенности задач динамического программирования вы знаете? Что называется управлением? В чем состоит метод динамического программирования? Сформулируйте принцип оптимальности Беллмана? Что называется сетью, звеньями? Что такое характеристика точки? Опишите алгоритм решения задачи определения кратчайшего расстояния по заданной сети? Практическая работа №7 «Нахождение кратчайших путей в графе. Решение задачи о максимальном потоке» Цель работы: Решить задачу о нахождении кратчайших путей в графе. Решить задачу о нахождении максимального потока. Краткая теория Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины, прилегающие к одному и тому же ребру, называются смежными. Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом. Если ребра не имеют ориентации, граф называется неориентированным. Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками, а ребра - линиями, соединяющими точки (рис. 1). Петля это дуга, начальная и конечная вершина которой совпадают. Простой граф - граф без кратных ребер и петель. Степень вершины это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер. Пустым называется граф без ребер. Полным называется граф, в котором каждые две вершины смежные. 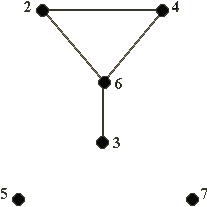 Рис. 1 Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей. Маршрут в графе путь, ориентацией дуг которого можно пренебречь. Цепь маршрут, в котором все ребра попарно различны. Цикл замкнутый маршрут, являющийся цепью. Маршрут, в котором все вершины попарно различны, называют простой цепью. Цикл, в котором все вершины, кроме первой и последней, попарно различны, называются простым циклом. Подграф графа это граф, являющийся подмоделью исходного графа, т.е. подграф содержит некоторые вершины исходного графа и некоторые ребра (только те, оба конца которых входят в подграф). Подграф называется остовным подграфом, если множество его вершин совпадает с множеством вершин самого графа. Граф называется связным, если любая пара его вершин связана. Связными компонентами графа называются подграфы данного графа, вершины которых связаны. Дерево — это связный граф без циклов. Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеалогические деревья. Граф без цикла называется лесом. Вершины степени 1 в дереве называются листьями. Деревья - очень удобный инструмент представления информации самого разного вида. Деревья отличаются от простых графов тем, что при обходе дерева невозможны циклы. Это делает графы очень удобной формой организации данных для различных алгоритмов. Очевидно, что графический способ представления графов непригоден для ПК. Поэтому существуют другие способы представления графов. В теории графов применяются Матрица инцидентности. Это матрица А с n строками, соответствующими вершинам, и m столбцами, соответствующего рёбрам. Для ориентированного графа столбец, соответствующий дуге (х,y) содержит - 1 в строке, соответствующей вершине х и 1, в строке, соответствующей вершине у. Во всех остальных 0. Петлю, т.е. дугу (х,х) можно представлять иным значением в строке х, например, 2. Если граф неориентированный, то столбец, соответствующий ребру (х,у) содержит 1, соответствующие х и у и нули во всех остальных строках. Матрица смежности. Это матрица n×n где n - число вершин, где bij = 1, если существует ребро, идущее из вершины х в вершину у и bij = 0 в противном случае. Нахождение минимального остова в графе Алгоритм решения Упорядочить ребра графа по возрастанию весов; Выбрать ребро с минимальным весом, не образующее цикл с ранее выбранными ребрами. Занести выбранное ребро в список ребер строящегося остова; Проверить, все ли вершины графа вошли в построенный остов. Если нет, то выполнить пункт 2. Нахождение кратчайшего пути в графе Пусть дан граф, дугам которого приписаны веса. Задача о нахождении кратчайшего пути состоит в нахождении кратчайшего пути от заданной начальной вершины до заданной конечной вершины, при условии, что такой путь существует. Данная задача может быть разбита на две: для начальной заданной вершины найти все кратчайшие пути от этой вершины к другим; найти кратчайшие пути между всеми парами вершин. Рассмотрим алгоритм решения для задачи первого типа: Необходимо найти путь от s - начальной вершины до t - конечной вершины. Каждой вершине присваиваем пометки I(Xi). I(s) = 0, I(Xi) равно бесконечности для всех Хi не равных s и считать эти пометки временными. Положить р = s. Для всех Хi, принадлежащих Г(р) и пометки которых временны, изменить пометки по следующему правилу: I(Xi) = min[I(Xi), I(p) + c(p, Xi)] среди всех вершин с временными пометками найти такую, для которой I(Xi*) = min[I(Xi)] считать пометку вершины Хi* постоянной и положить р = Хi*. если р = t, то I(р) является длинной кратчайшего пути, если нет, перейти к шагу 2. Как только все пометки расставлены, кратчайшие пути получают, используя соотношение I(Xi') + c(Xi',Xi) = I(Xi) (1). Для решения задачи второго типа можно применять данный алгоритм для каждой вершины. Порядок выполнения заданий Задача 1. Составить матрицы инцидентности и смежности для графа: 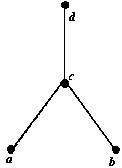 Решение.
Задача 2. На представленном графе найдите: а) минимальный остов дерева, б) найдите кратчайший путь от начальной точки Х1 до всех остальных точек. 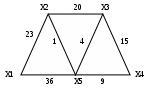 |