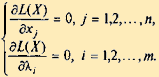ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы

• Название: Методические указания по выполнению практических работ по дисциплине Математические методы
• Дата: 19.09.2022
• Размер: 1.97 Mb.
• Имя файла: Метод указ по мат методам.doc
• Тип: Методические указания; #685112
• страница: 10 из 14

Необходимое условие экстремума.

Если в точке X* функция Z = f (Х) имеет экстремум, то частные производные функции в этой точке равны 0:

f '_x1 (X*) = 0, i = 1, 2, ..., n.

Следовательно, точки экстремума функции Z = f (Х) удовлетворяют системе уравнений:

(6)

Для получения достаточных условий следует определить в стационарной точке знак дифференциала второго порядка. Дифференциала второго порядка обозначается d²f (х₁ , х₂ , …, х_n ) f '_x1 (X) найти частную производную по переменной х_j , то получим частную производную второго порядка по переменным х_i , х_j , которая обозначается f ''_{xi, xj} (X). В этом случае



Достаточные условия экстремума.

Двух переменных:

• 
  если Δ > 0 и а₁₁ < 0 (а₂₂ < 0), то в точке Х ⁰ функция имеет максимум:
  если Δ > 0 и а₁₁ > 0 (а₂₂ > 0),то в точке Х ⁰ – минимум (в этих случаях Х ⁰ = Х*);
  
• 
  если Δ < 0, то экстремума нет;
  
• 
  если Δ = 0, то вопрос об экстремуме остается открытым.
  

Метод множителей Лагранжа

Способ определения условного экстремума начинается с построения вспомогательной функции Лагранжа, которая в области допустимых решений достигает максимума для тех же значений переменных x₁, x₂, ..., x_n, что и целевая функция z.
Пусть решается задача определения условного экстремума функции z = f (X) при ограничениях φ_i(x₁, x₂, ..., x_n ) = 0, i = 1, 2, ..., m, m < n

Составим функцию

(7)

которая называется функцией Лагранжа. X, — постоянные множители (множители Лагранжа). Отметим, что множителям Лагранжа можно придать экономический смысл. Если f (x₁, x₂, ..., x_n ) — доход, соответствующий плану X = (x₁, x₂, ..., x_n ), а функция φ_i (x₁, x₂, ..., x_n ) — издержки i-го ресурса, соответствующие этому плану, то X, — цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса (маргинальная оценка). L(Х) — функция n + m переменных (x₁, x₂, ..., x_n , λ₁, λ₂, ..., λ_n ). Определение стационарных точек этой функции приводит к решению системы уравнений

(8)

Легко заметить, что . Таким образом, задача нахождения условного экстремума функции z = f (X) сводится к нахождению локального экстремума функции L(X). Если стационарная точка найдена, то вопрос о существовании экстремума в простейших случаях решается на основании достаточных условий экстремума — исследования знака второго дифференциала d²L(X) в стационарной точке при условии, что переменные приращения Δx_i - связаны соотношениями

(9)

полученными путем дифференцирования уравнений связи.
Решение системы нелинейных уравнений с двумя неизвестными

с помощью средства Поиск решения

Настройка Поиск решения позволяет находить решение систе­мы нелинейных уравнений с двумя неизвестными: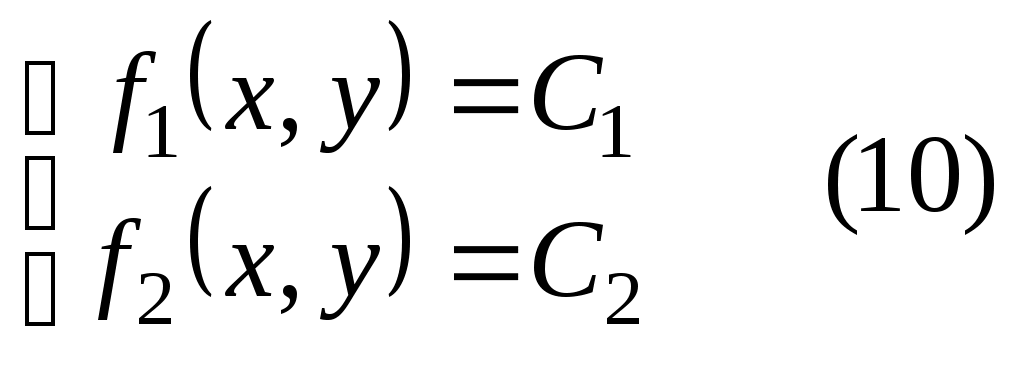



где - нелинейная функция от переменных xи y, - произвольная постоянная.

Известно, что пара (x, y) является решением системы уравнений (10) тогда и только тогда, когда она является решением следующего уравнение с двумя неизвестными:



С другой стороны, решение системы (10) — это точки пересечения двух кривых: f_](x,y) = Cи f₂(х, у) = С₂на плоскости ХОY.

Из этого следует метод нахождения корней системы. нелинейных уравнений:

1. 
   Определить (хотя бы приближенно) интервал существования решения системы уравнений (10) или уравнения (11). Здесь не­обходимо учитывать вид уравнений, входящих в систему, область определения каждого их уравнений и т. п. Иногда применяется подбор начального приближения решения;
   
2. 
   Протабулировать решение уравнения (11) по переменным x и y на выбранном интервале, либо построить графики функций f₁(x,y) = С, и f₂(х,у) = С₂(система(10)).
   
3. 
   Локализовать предполагаемые корни системы уравнений — найти несколько минимальных значений из таблицы табулирование­ корней уравнения (11), либо определить точки пересечения кривых, входящих в систему (10).
   

4. Найти корни для системы уравнений (10) с помощью надстройки Поиск решения.
Порядок выполнения заданий

Задача. Решить систему нелинейных уравнений:



Решение:

Легко видеть, что решение системы уравнений являются точки пересечения окружности (с радиусом 2 и центром (1,-1)) и прямой .

Данную систему заменим равносильным уравнением:

, для которого будем искать решения с площадью надстройки Поиск решения.

1. 
   Исходя из графиков уравнений, интервал локализации корней определим в границах от -3 до 3 (рис. 1). Ячейка В3:В43 содержат значения Х. Формулы для построения графиков:
   

• 
  В ячейке С3:
  

=-1+корень(4-(В3-1)^2)

• 
  В ячейке D3:
  

=-1-корень(4-(В3-1)^2)

• 
  В ячейке Е3: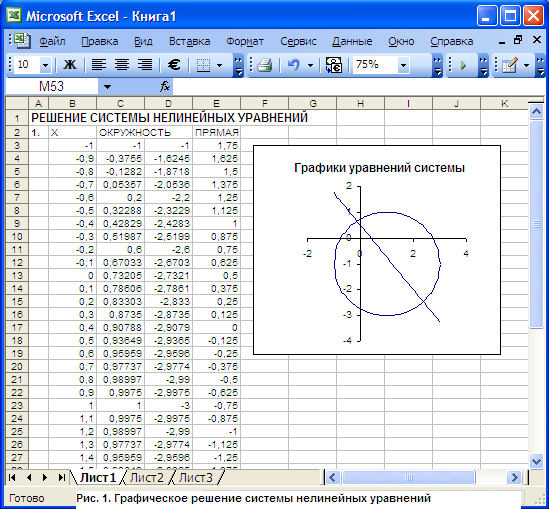
  

= (2-5*В3)/4

2. 
   Табулируем равносильное уравнение на отрезке [-3; 3] с шагом 0,5 (рис. 2).
   

3. 
   Локализируем корни равносильного уравнения (рис. 3):
   
   • 
     Ячейки А47:А59 содержат значения X на отрезке [-3; 3] с шагом 0,5;
     
   • 
     Ячейки B46:N46 содержат значения Y на отрезке [-3; 3] с шагом 0,5;
     
   • 
     Формула для ячейки В47 (копируется на диапазон B47:N59):
     

=(($A47-1)^2+(B$46+1)^2-4)^2+(5*$A47+4*B$46-2)^2

• 
  Формула для ячейки В62 (копируется на диапазон B62:N62):
  

=МИН(В47:В59)

Исходя из результатов вычислений, определим следующие пары предполагаемых корней уравнения: (2,5; -2,5), (2; -2), (0; 0,5), (0; 1).

4. 
   Найдем корни равносильного уравнения (рис. 4) – для этого поместим пары значений для предполагаемых корней в ячейки D69:E72. В ячейку G69 введем формулу для равносильного уравнения (копируется на диапазон G69:G72):
   

=((D69-1)^2+(E69+1)^2-4)^2+(5*D69+4*E69-2)^2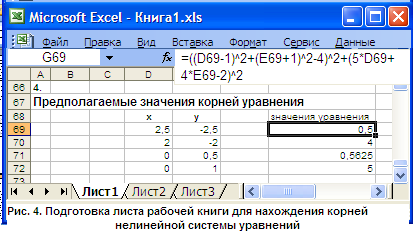


С помощью надстройки Поиск решения (в окне Параметры поиска решения флажок Линейная модель должен быть снят) установим необходимые параметры для поиска корня равносильного уравнения (рис. 5),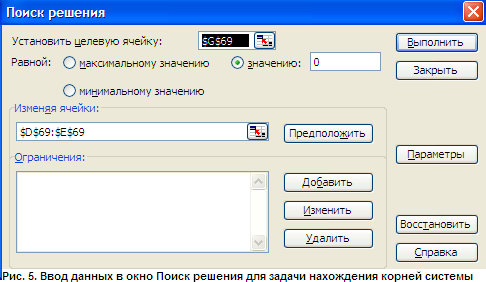



Затем выполним поиск решения. Процедуру повторим для всех имеющихся пар корней.

Результаты поиска решения (рис. 6) позволяют делать вывод о том, что система имеет 2 решения:

(2,3675745729901; -2,45934248863711) и (-0,123564081639673; 0,654434224216163)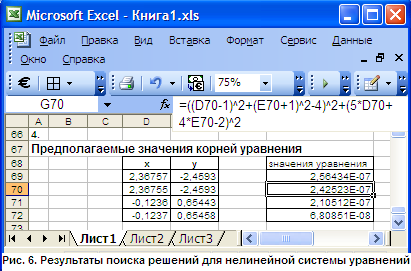



Задания для самостоятельной работы

1 вариант.

Задача. Решить систему нелинейных уравнений:


2 вариант.

Задача. Решить систему нелинейных уравнений:



3 вариант.

Задача. Решить систему нелинейных уравнений:


4 вариант.

Задача. Решить систему нелинейных уравнений:


5 вариант.

Задача. Решить систему нелинейных уравнений:


Контрольные вопросы

1. 
   Какие задачи называются задачами нелинейного программирования?
   
2. 
   Как записывается общая формулировка нелинейных задач?
   
3. 
   Как выглядит классификация задач нелинейного программирования?
   
4. 
   В чем суть метода множителей Лагранжа?
   
5. 
   Какие способы решения нелинейных задач вы знаете?
   

Практическая работа №6

«Решение простейших задач методом динамического программирования –

задача о распределении средств между предприятиями,

задача определения кратчайших расстояний по заданной сети»

Цель работы: Решить простейшие задачи методом динамического программирования.

Краткая теория

Динамическое программирование – метод оптимизации, приспособленный, к задачам, в которых процесс принятия решения может быть разбит на отдельные этапы (шаги). Такие задачи называются многошаговыми.

Характерные особенности задач динамического программирования:

1. 
   Неоднозначность решения.
   
2. 
   Возможность деления вычислительного процесса на этапы.
   
3. 
   Общий критерий – сумма частных критериев на этапах.
   

Динамическое программирование позволяет осуществлять опти­мальное планирование многошаговых процессов, зависящих от времени. Процесс называется управляемым, если можно влиять на ход его развития. Управлением называется совокупность решений, принимаемых на каждом этапе для влияния на ход процесса. Началом этапа (шага) управляемого процесса считается момент принятия решения. Планируя многошаговый процесс, исходят из интересов всего процесса в целом, всегда необходимо иметь в виду конечную цель.

Метод динамического программирования состоит в том, что опти­мальное управление строится постепенно. На каждом этапе оптимизируется управление только этого этапа, причем управление выбирается с учётом последствий, т.е. оптимальное управление для данного этапа должно учитывать весь последующий ход процесса, для чего необходимо знать все управления на последующих этапах. Поскольку процесс заканчивается на последнем этапе, оптимальное решение не должно учитывать последующего управления. Таким образом, процесс вычисления протекает в обратном направлении, от конца к началу.

Постановка задачи динамического программирования.

Пусть - состояния системы на начальном, k-ом и конечном этапе, - управления системой на начальном, k-ом и конеч­ном этапах. Управление переводит систему из состояния в со­стояние . Показатель эффективности на k-ом этапе обозначим через .

Так как оптимизацию показателя эффективности начинаем с последнего этапа, то, зная максимум показателя эффективности на п-ом шаге



найдем максимум показателя эффективности на (п-1)- ом шаге

,

где называется "сиюминутной" выгодой на (п-1)- ом шаге.

Основное функциональное уравнение динамического программирования (уравнение Беллмана) имеет вид:



Принцип оптимальности Беллмана можно сформулировать следую­щим образом: каковы бы не были начальное состояние и начальное реше­ние, последующее решение должно быть оптимальным по отношению к состоянию, полученному в результате начального решения. Иными слова­ми, принцип оптимальности утверждает, что если в данный момент выбра­но не наилучшее решение, то последствия этого нельзя исправить в буду­щем.