ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb.
|
|
б) Всякую задачу линейного программирования можно сформулировать в стандартной форме. Преобразование задачи на минимум в задачу на максимум, а также обеспечение не отрицательности переменных производится так же, как и раньше. Всякое равенство в системе ограничений равносильно системе взаимопротивоположных неравенств, тогда получим: 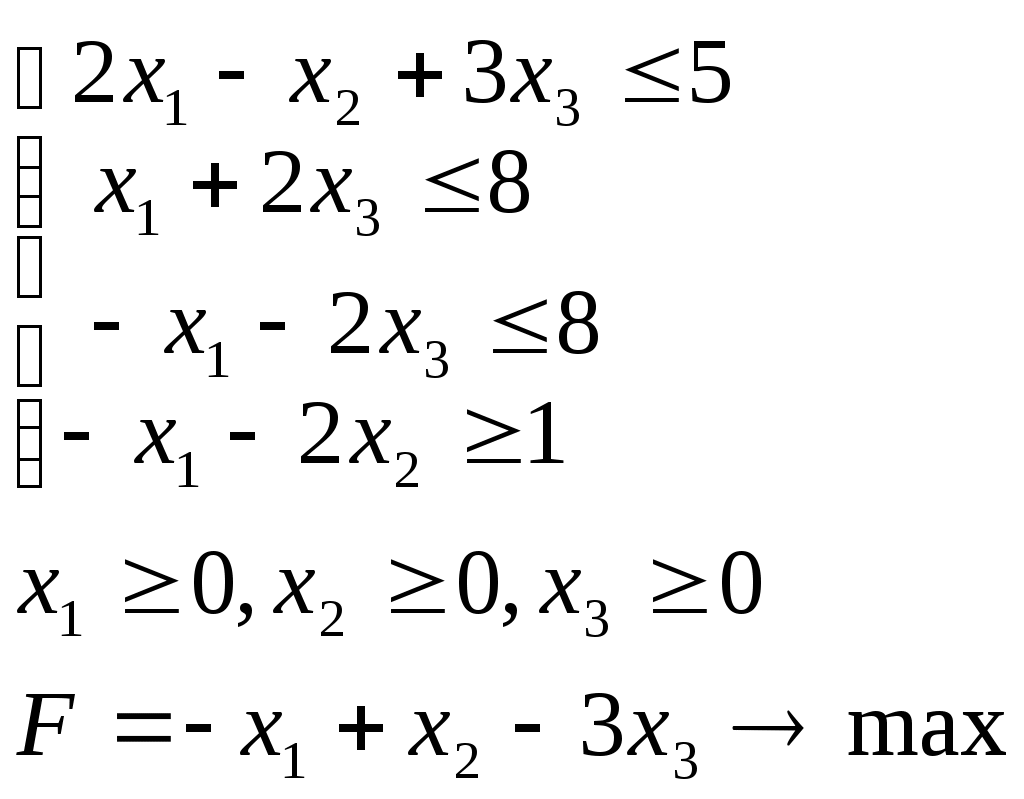 Задание 2. Для производства двух видов, изделии  и  используется, три вида сырья  , запасы которого соответственно равны 100, 60, 180 единиц. Для производства одной единицы продукции используется 2 единицы сырья  и по 1 единице сырья  . Для производства одной единицы продукции используется по 1 единице сырья  и 4 единицы сырья  . Прибыль от реализации 1 единицы каждой продукции и соответственно равна 30 и 20 единиц. Необходимо составить симплекс-методом такой план выпуска продукции и , при котором суммарная прибыль будет наибольшей.Решение. 1. Составим математическую модель задачи: Пусть х1 – единица готовой продукции вида ,x2 - единица готовой продукции вида ,Цель фабрики получить максимальную прибыль от реализации всей продукции видов и , тогда: Система ограничений: 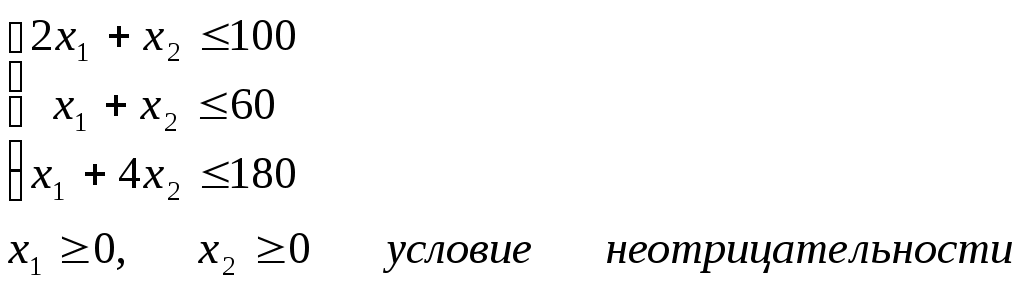 Задачу приводим к каноническому виду: 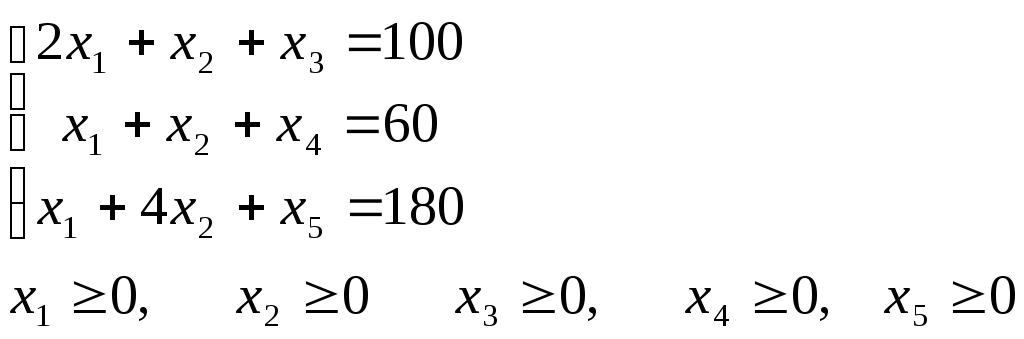 Базисные переменные выражаем через свободные: 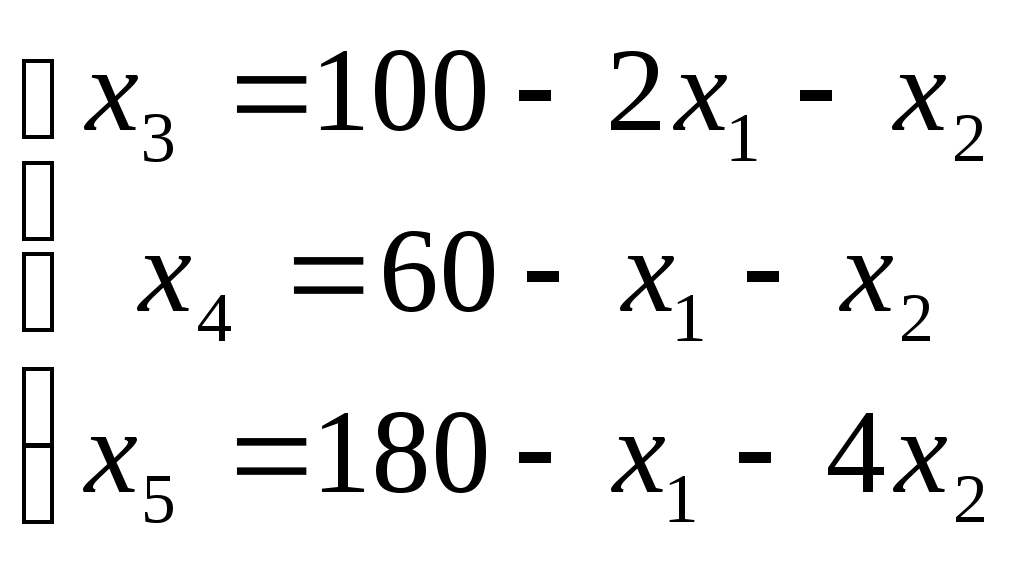 Записываем начальный план:  Строим первую симплекс-таблицу: Т  аблица 1. Первая симплекс-таблица
Начальный план не оптимален, так как в F-строке есть отрицательные элементы. Улучшение плана. Строим вторую симплекс-таблицу, элементы которой пересчитываем по соответствующим формулам. Т  аблица 2. Вторая симплекс-таблица
План, соответствующий таблице 2,  не оптимален, так как в F-строке есть отрицательные элементы. Улучшаем его.Улучшение плана. Строим третью симплекс-таблицу, элементы которой пересчитываем по соответствующим формулам. Таблица 3. Третья симплекс-таблица
План, соответствующий таблице 3,  оптимален, так как в F-строке нет отрицательных элементов.Ответ: если предприятие будет выпускать продукцию вида и в количестве 40 и 20 единиц соответственно, то получит максимальную прибыль в размере 1600 единиц, при этом сырье будет израсходовано полностью, а сырье останется в количестве 60 единиц.Задания для самостоятельной работы 1 вариант. Задача 1. а) Привести к канонической форме задачу линейного программирования. 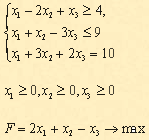 б) Напишите задачу в стандартной форме. Задача 2. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В симлекс-методом. а1= 19, а2= 16, а3= 19, b1= 31, b2= 9, b3= 1, c1= 1121, c2= 706, c3= 1066, α=16, β=19. 2 вариант. Задача 1. а) Привести к канонической форме задачу линейного программирования. 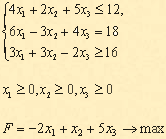 б) Напишите задачу в стандартной форме. Задача 2. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В симплекс-методом. а1= 14, а2= 15, а3= 20, b1= 40, b2= 27, b3= 4, c1= 1200, c2= 993, c3= 1097, α=5, β=13. 3 вариант. Задача 1. а) Привести к канонической форме задачу линейного программирования. 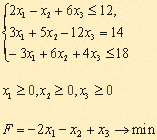 б) Напишите задачу в стандартной форме. Задача 2. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В симплекс-методом. а1= 14, а2= 15, а3= 20, b1= 40, b2= 27, b3= 4, c1= 1200, c2= 993, c3= 1097, α=5, β=13. 4 вариант. Задача 1. а) Привести к канонической форме задачу линейного программирования. 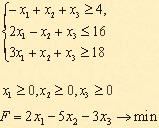 б) Напишите задачу в стандартной форме. Задача 2. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В симплекс-методом. а1= 9, а2= 15, а3= 15, b1= 27, b2= 15, b3= 3, c1= 606, c2= 802, c3= 840, α=11, β=6. |
