ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb.
|
|
5 вариант. Задача 1. а) Привести к канонической форме задачу линейного программирования. 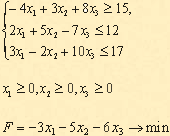 б) Напишите задачу в стандартной форме. Задача 2. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В симплекс-методом. а1= 13, а2= 13, а3= 11, b1= 23, b2= 11, b3= 1, c1= 608, c2= 614, c3= 575, α=5, β=7. Контрольные вопросы Какие задачи можно отнести к задачам линейного программирования? Какова основная идея линейного программирования? Что образует систем ограничений? Что называется допустимым планом? Что называется целевой функцией? Как записывается общая форма задачи линейного программирования? Как строится каноническая форма ЗЛП? Как перевести ЗЛП в стандартную форму? Какова идея симплекс-метода? В чем суть условия оптимальности плана? Из каких пунктов состоит алгоритм решения ЗЛП симплекс-методом? Что такое симплекс-отношение? Практическая работа №4 «Нахождение начального решения транспортной задачи. Решение транспортной задачи методом потенциалов» Цель работы: Найти начальное решение транспортной задачи двумя методами: методом северо-западного угла и методом наименьшей стоимости. Найти оптимальное решение транспортной задачи методом потенциалов. Краткая теория Симплексный метод для решения задач линейного программирования является универсальным, он позволяет решить любую задачу, но решение иных задач связано с трудоемкими расчетами. Можно выделить класс задач, которые решаются более простыми специальными методами. К числу таких задач относятся так называемые транспортные задачи. Классическая транспортная задача - о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов отправления в пункты назначения. Классическая транспортная задача (сокращенно ТЗ) формулируется следующим образом. В пунктах отправления  , которые будем называть также поставщиками, сосредоточены запасы однородного груза в количествах  соответственно. В пункты назначения  , именуемые потребителями, надлежит доставить соответственно  единиц груза.Известен транспортный тариф  - стоимость перевозки единицы груза из пункта  в пункт  ,  . Требуется составить такой план перевозок груза, при котором общая стоимость F всех перевозок была бы наименьшей, при этом все заявки были бы выполнены. В термин "транспортный тариф" вкладывается условное понимание стоимости единицы груза - это может быть себестоимость, расстояние, тариф, время, расход топлива или электроэнергии и др. Пусть суммарные запасы грузов у поставщиков равны суммарным потребностям потребителей:  Это условие называется условием баланса. Если для ТЗ условие баланса выполняется, то модель ТЗ называется закрытой, если условие баланса не выполнено, то модель ТЗ - открытая. Составим математическую модель ТЗ. Пусть  - количество груза, которое поставщик отправляет потребителю ( ) со стоимостью перевозок . Данные задачи можно представить в виде таблицы 1.Таблица 1.
По смыслу своему величины  и должны удовлетворять следующим ограничениям:Из пункта все запасы должны быть вывезены (ограничения по ресурсам):  ;Заявки потребителей должны быть выполнены (ограничения по потребностям):  .Затраты на перевозку  единиц груза из пункта поставки в пункт потребления составляют  рублей; общая же стоимость всех перевозок равна сумме всех таких затрат:  Математическая постановка ТЗ состоит в следующем: составить план перевозок 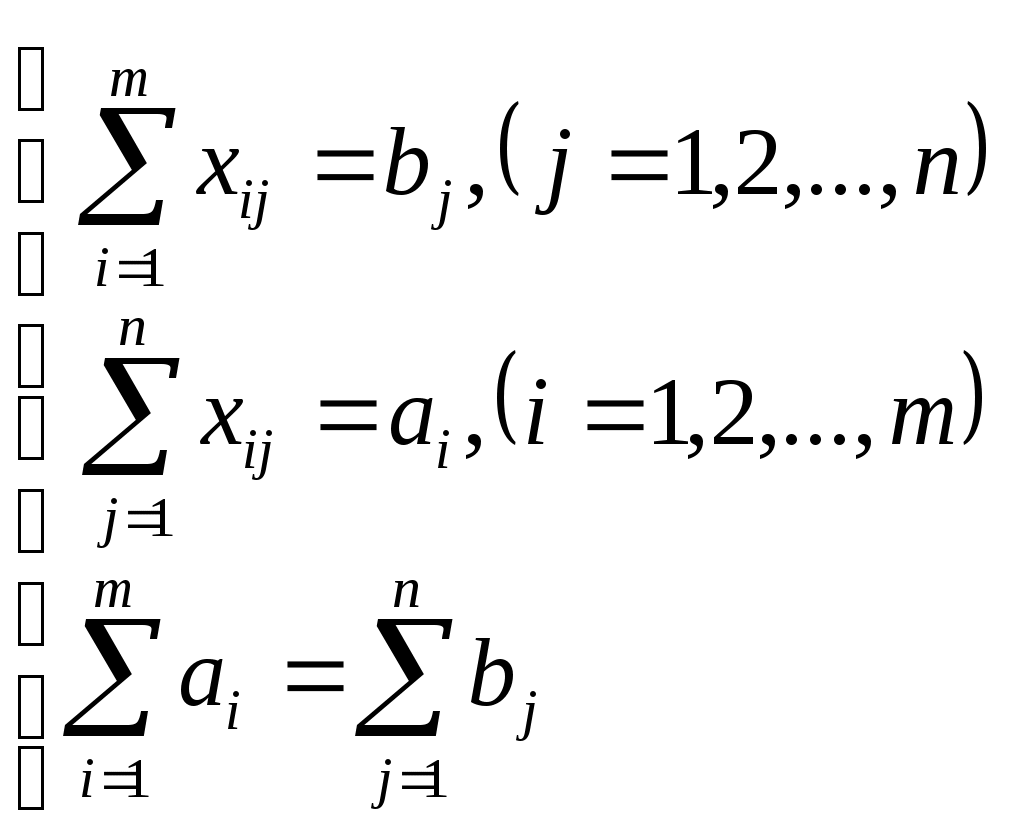, удовлетворяющих системе ограничении: ,условию неотрицательности: , , при котором целевая функция достигает своего минимума: Из математической модели видно, что ТЗ является частным случаем общей задачи линейного программирования. В общей теории линейного программирования доказаны следующие теоремы: Теорема 1. Транспортная задача при выполнении условия баланса всегда имеет решение. Теорема 2. Система ограничений транспортной задачи содержит т+п-1 линейно-независимых уравнений. При решении задач практический смысл теоремы 2 заключается в следующем: число назначенных перевозок равно т+п-1. Процедура решения ТЗ будет состоять в последовательном улучшении опорных планов и проверки их на оптимальность. Методы построения начального плана. Существует несколько методов построения первоначального опорного плана ТЗ (опорный план - план, удовлетворяющий системе ограничений и условию неотрицательности). Рассмотрим только два из них: метод северо-западного угла и метод наименьшей стоимости. Как уже отмечалось, в опорном плане не более r = m + n - 1 переменных ,отличных от нуля. Если таких переменных равно r, то такой план называют невырожденным, в противном случае - вырожденным. Метод северо-западного угла.Назначение перевозок начинаем с левой верхней клетки (северо-западный угол). Сравнивая ресурсы поставщика и потребности потребителя, назначаем максимально возможную перевозку. Если ресурсов поставщика недостаточно, то переходим к следующему поставщику. Если ресурсов у поставщика достаточно, то назначив нужную перевозку первому потребителю, переходим к следующему потребителю. При назначении перевозок для удобства записываем остаток ресурсов (потребностей); если ресурсы закончились или потребности удовлетворены, то ставим букву "к" (конец). Если при назначении перевозки одновременно закончились запасы ресурсов у поставщика и удовлетворены потребности потребителя, то из "игры" выводим только одного участника, другому оставляем нуль запасов или нуль потребностей. Метод наименьшей стоимости. Выбираем клетку с наименьшей тарифной ставкой и назначаем максимально возможную перевозку. Если запасы закончились или потребности удовлетворены, то поставщика или потребителя исключаем. Среди оставшихся клеток снова выбираем клетку с наименьшей стоимостью и назначаем максимально возможную перевозку. Если в результате назначения перевозки закончились запасы поставщика или удовлетворены потребности потребителя, то его исключаем из дальнейшего рассмотрения. Метод потенциалов построения оптимального плана. Наиболее простым методом решения ТЗ является метод потенциалов. Потенциалами называются условные числа  приписанные определенным образом каждому поставщику и потребителю. Теорема 3( условие оптимальности плана). Сумма потенциалов поставщика и потребителя равна тарифной ставке для занятых клеток; сумма потенциалов поставщика и потребителя не превышает тарифную ставку для свободных клеток:  | ||||||||||||||||||||||||||||||||||||||||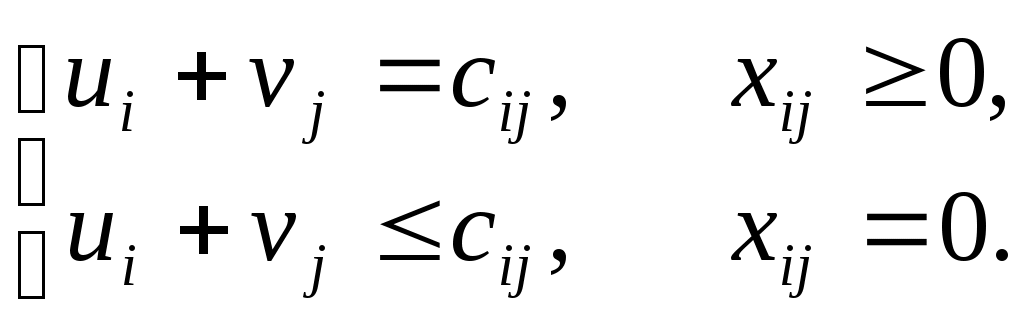
