ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb.
|
|
Алгоритм решения: Используя систему ограничений и условия неотрицательности, строим область допустимых решений. Строим линию уровня  . Линией уровня функции двух переменных называется линия, вдоль которой функция сохраняет свое постояное значение.Строим градиент целевой функции. Градиент функции - это вектор, имеющий своими координатами частные производные функции и показывающий направление наискорейшего роста значения функции. Так как целевая функция ЗЛП линейная, то линии уровня целевой функции - прямые и  , п- вектор нормали к этим прямым. : . Перемещаем линию уровня вдоль градиента функции. Если ЗЛП на минимум, то оптимальное решение находится в первой точке, принадлежащей ОДР; если ЗЛП на максимум, то оптимальное решения находится в последней точке, принадлежащей ОДР.Замечание. При построении ОДР возможны случаи: ОДР оказалась пустым множеством. В этом случае ЗЛП не имеет решения из-за несовместности системы ограничений. ОДР оказалась либо выпуклым многоугольником, либо не ограниченной выпуклой многоугольной областью. Тогда ЗЛП имеет оптимальное решение, которое совпадает по крайней мере с одной из вершин ОДР. Используя алгоритм решения и систему ограничений и условия неотрицательности, построим ОДР. Для этого во всех неравенствах системы ограничений и условия неотрицательности знак неравенства заменим на знак равенства. В результате будем иметь уравнения прямых: 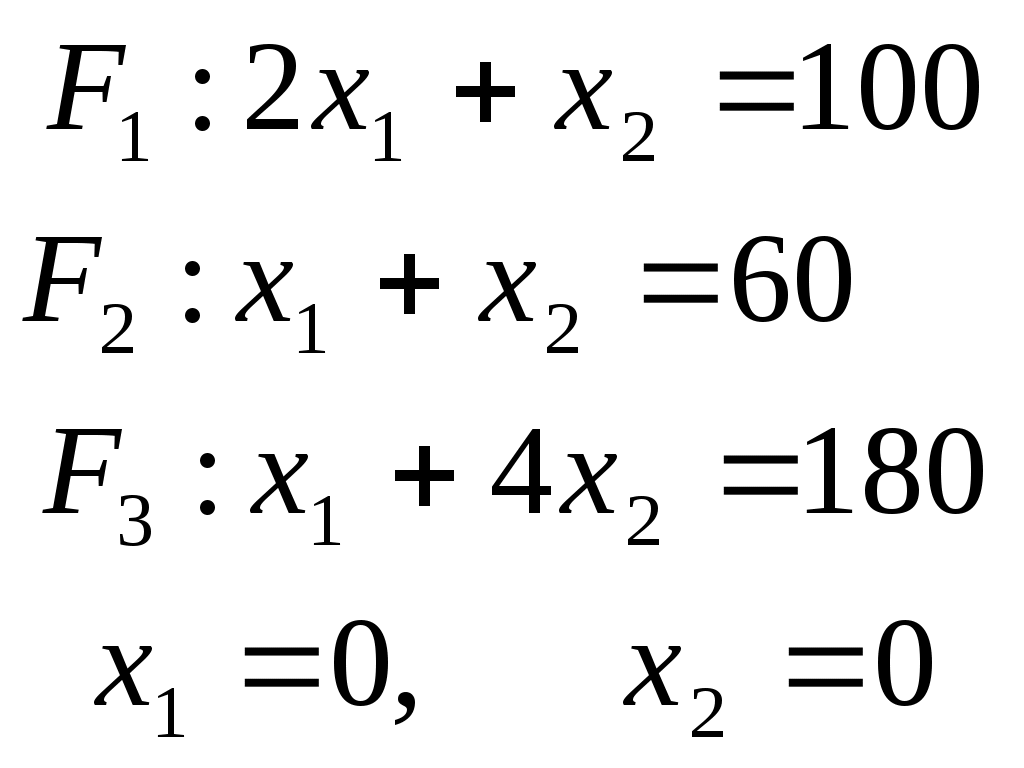 В системе координат 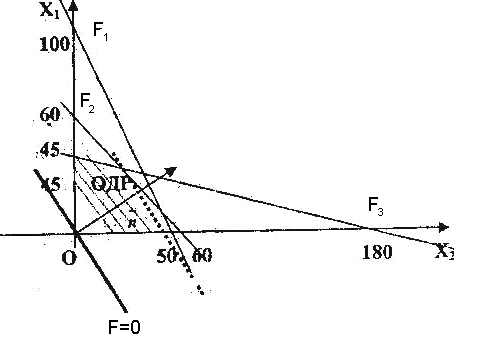 построим эти прямые. В результате будем иметь ОДР. В этой же системе координат строим линию уровня и вектор  Так как задача на максимум, будем перемещать линию уровня F=0 вдоль вектора n до тех пор, пока она не пересечет ОДР в самом крайнем своем положении, т.е. при дальнейшем перемещении она не будет с ОДР иметь общие точки. Такой точкой оказалась точка пересечения прямых  и  .Вычислим ее координаты. 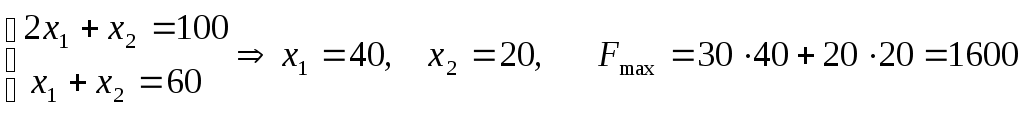 Таким образом, если предприятие будет выпускать продукцию вида  и  , в количестве 40 и 20 единиц соответственно, то получит максимальную прибыль в размере 1600 единиц. Задание 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки.   Задания для самостоятельной работы 1 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 19, а2= 16, а3= 19, b1= 26, b2= 17, b3= 8, c1= 868, c2= 638, c3= 853, α=5, β=4. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев  и  и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида  и  .Значения  и  заданы таблицей:
2 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 14, а2= 15, а3= 20, b1= 40, b2= 27, b3= 4, c1= 1200, c2= 993, c3= 1097, α=5, β=13. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев и и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида и .Значения и заданы таблицей:
3 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 9, а2= 15, а3= 15, b1= 27, b2= 15, b3= 3, c1= 606, c2= 802, c3= 840, α=11, β=6. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев и и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида и .Значения и заданы таблицей:
4 вариант. Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 13, а2= 13, а3= 11, b1= 23, b2= 11, b3= 1, c1= 608, c2= 614, c3= 575, α=5, β=7. Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки. А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев и и определить минимальное решение.Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида и .Значения и заданы таблицей:
|
