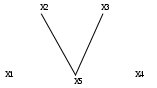ппп. Метод указ по мат методам. Методические указания по выполнению практических работ по дисциплине Математические методы
 Скачать 1.97 Mb. Скачать 1.97 Mb.
|
|
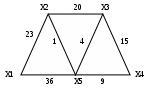
Решение. а) Найдем минимальный остов дерева представленного на рисунке. Составим таблицу значений расстояний между точками.
Для решения данной задачи достаточно рассмотреть или только левую или только правую часть от главной диагонали матрицы. Воспользуемся левой частью таблицы. А также изобразим исходный график без ребер, только с помощью одних вершин.
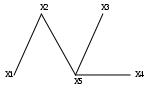
Из элементов матрицы выбираем минимальный - (Х2,Х5) = 1. Обводим выбранный элемент кружком и указываем на рисунке соответствующее ребро.
Из оставшихся элементов выбираем минимальный - (Х3,Х5) = 4. Элемент обводим кружком. Чтобы выполнялось условие 2 пункты Х2 и Х3 не должны соединяться, поэтому элемент (Х2,Х3) зачёркивается. И т.д.
В итоге получаем:
Длина минимального остова равна (Х1,Х2)+(Х2,Х5)+(Х3,Х5)+(Х4,Х5)=23+1+4+9=37 Б) Найдем кратчайший путь представленного графа от начальной точки Х1 до всех остальных точек.
Начальное расстояние I(X1)=0*, I(Xi)=∞, Xi≠X1, p=X1. Находим множество точек, соединяющиеся с точкой Х1: Г{X1}={X2,X5} Находим минимальное расстояние каждой из этих точек: I(X2)=min[∞,0*+23]=23, I(X5)=min[∞,0*+36]=36, min[I(X2), I(X3), I(X4), I(X5)]=min[23, 36, ∞, ∞]=23, X2: I(X2)=23*, p=23, рядом с точкой Х2 поставим расстояние 23. Находим множество точек, соединяющиеся с точкой Х2, точку Х1 не трогаем, так как мы ее уже рассмотрели. Г{X2}={X3,X5} Находим минимальное расстояние каждой из этих точек: I(X3)=min[∞,23*+20]=43, I(X5)=min[36,23*+1]=24, min[I(X3), I(X4), I(X5)]=min[43,∞, 24]=24, X5: I(X5)=24*, p=24, рядом с точкой Х5 поставим расстояние 24. Аналогично находим все остальные расстояния до остальных точек: Г{X5}={X3,X4} Находим минимальное расстояние каждой из этих точек: I(X3)=min[43,24*+4]=28, I(X4)=min[∞,24*+9]=33, min[I(X3), I(X4)]=min[28, 33]=28, X3: I(X3)=28*, p=28, рядом с точкой Х3 поставим расстояние 28. Г{X3}={X4} Находим минимальное расстояние до этой точки: I(X4)=min[33,28*+15]=33, X4: I(X4)=33*, p=33, рядом с точкой Х4 поставим расстояние 33. 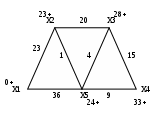 Запишем ответ в виде таблицы кратчайших расстояний от точки Х1 до всех остальных точек графа.
Задания для самостоятельной работы 1 вариант Задача 1. Составить матрицы инцидентности и смежности для графа: 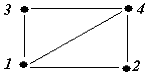 Задача 2. На представленном графе найдите: а) минимальный остов дерева, б) найдите кратчайший путь от начальной точки Х1 до всех остальных точек. 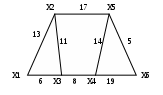 2 вариант Задача 1. Составить матрицы инцидентности и смежности для графа:  Задача 2. На представленном графе найдите: а) минимальный остов дерева, б) найдите кратчайший путь от начальной точки Х1 до всех остальных точек. 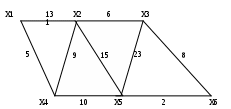 3 вариант Задача 1. Составить матрицы инцидентности и смежности для графа: 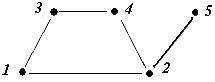 Задача 2. На представленном графе найдите: а) минимальный остов дерева, б) найдите кратчайший путь от начальной точки Х1 до всех остальных точек.  4 вариант Задача 1. Составить матрицы инцидентности и смежности для графа: 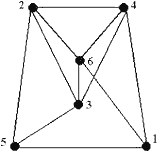 Задача 2. На представленном графе найдите: а) минимальный остов дерева, б) найдите кратчайший путь от начальной точки Х1 до всех остальных точек. 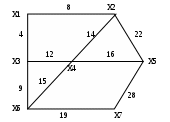 5 вариант Задача 1. Составить матрицы инцидентности и смежности для графа:  Задача 2. На представленном графе найдите: а) минимальный остов дерева, б) найдите кратчайший путь от начальной точки Х1 до всех остальных точек. 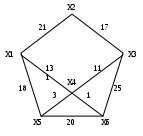 Контрольные вопросы Дайте определение граф. В чем состоит отличие ориентированного графа от неориентированного графа? В чем отличие пустого графа от простого графа? Как определить степень вершины? Чем отличается цепь в графе от цикла? Дайте понятие подграф графа. В чем суть связанного графа? Как находятся матрицы инцидентности и матрицы смежности? Как найти минимальный остов дерева? Как найти кратчайшее расстояние в графе? |




 0
0