определение среднего времени безотказной работы. Методические указания составлены на основе Требований к разработке методических указаний для студентов по проведению лабораторных работ и практических занятий

• Название: Методические указания составлены на основе Требований к разработке методических указаний для студентов по проведению лабораторных работ и практических занятий
• Анкор: определение среднего времени безотказной работы
• Дата: 15.12.2021
• Размер: 0.74 Mb.
• Имя файла: 00140318-120ab073.docx
• Тип: Методические указания; #305158
• страница: 4 из 9

Решение.

1. 
   Получение простого статистического ряда
   

Определяем наработку до отказа по всем объектам. Для этого из каждого последующего времени возникновения отказа вычитаем предыдущее. Для удобства расчетов данные представляем в виде таблицы.


Таблица 5.2. – Нахождение значений наработки на отказ

№ изделия	Т1	Т2	Т3	Т4	Т5	Т6	Т7	Т8
1	2	3	4	5	6	7	8	9
1	155	136	49	56	504	245
2	90	90	280	393	908	226
3	420	510	283	703	89	769	241
4	300	530	600	503	314	721	252	341
5	301	309	1090	200	200	150
6	68	347	473	343	486	200	173	877
7	87	124	504	885	303	212	229	554
1	2	3	4	5	6	7	8	9
8	60	220	115	75	380	200	950
9	50	108	326	461	175	180
10	81	159	553	352	636	192	32	495

Выстраиваем полученные данные в порядке возрастания. Находим максимальное и минимальное значение из полученного простого статистического ряда.

^Tmin ^Tmax

 32 ч

 1090 ч

Определяем диапазон значений или амплитуду статического ряда.

  T_max T_min 1090  32 1058ч

2. 
   Обработка статистического ряда
   

Количество данных равно 70. Определяем количество интервалов.

N  70

k N

70  8 _.

Определяем длину интервала

T  ^

k

 ¹⁰⁵⁸  132, 25  140 ч

8

Рассчитываем частость и накопленную частость по всем интервалам. Данные сводим в таблицу 5.3.

Таблица 5.3. – Расчет частости и накопленной частоты

No интервала	Начало интервала в час.	Конец интервала в час.	Кол-во изд. отказав. в интервале, Δni(Δti)	Частость, Δn(Δt)/N	Накопленная частость, Σ(Δn(Δt)/N)
1	30	170	19	0,27	0,27
2	170	310	21	0,30	0,57
3	310	450	9	0,13	0,70
4	450	590	11	0,16	0,86
5	590	730	4	0,06	0,91
6	730	870	1	0,01	0,93
7	870	1010	4	0,06	0,99
8	1010	1150	1	0,01	1,00

Σ=70

Σ=1,00

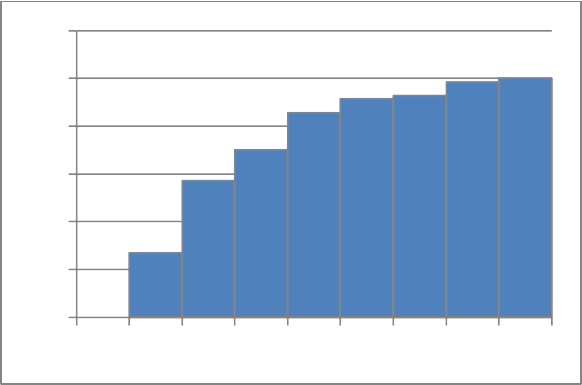
Строим гистограммы по полученным значениям частости и накопленной частости

0,35

0,3

0,25

0,2

0,15

0,1

0,05

0

30 170 310 450 590 730 870 1010

1,2




1

0,8

0,6

0,4

0,2

0

30 170 310 450 590 730 870 1010

Рисунок 5.1 – Гистограмма частости Рисунок 5.2 – Гистограмма накопленной частости

3. 
   Расчет показателей безотказности по статистическим данным
   

Определяем количество работоспособных изделий на середину каждого периода по формуле

N t   N  nt 

Определяем статистическую оценку вероятности безотказной работы на середину каждого периода по формуле


R
_{t  1} ^{nt }_ ^{N t }_.

N N

Определяем количество отказавших деталей нарастающим итогом на середину каждого периода по формуле

nt_i1   nt nt

Определяем статистическую оценку вероятности отказа на середину каждого периода по формуле


Q
_{t } nt _.

N

Определяем статистическую оценку плотности вероятности отказов по формуле


f
_t nt _.

Nt

Результаты расчета для удобства сводим в таблицу 5.4
Таблица 5.4. – Расчет показателей безотказности по экспериментальным данным

Начало интервал а	Конец интервал а	Середина интервала	Количество отказавших изделий в интервале	Количеств о отказавши х изделий на середину интервала	Количество работоспособ ных изделий на середину интервала	R(t)	Q(t)	f(t)
1	2	3	4	5	6	7	8	9
30	170	100	19	9,5	60,5	0,86	0,14	0,00097
170	310	240	21	29,5	40,5	0,58	0,42	0,00301
310	450	380	9	44,5	25,5	0,36	0,64	0,00454
1	2	3	4	5	6	7	8	9
450	590	520	11	54,5	15,5	0,22	0,78	0,00556
590	730	660	4	62	8	0,11	0,89	0,00633
730	870	800	1	64,5	5,5	0,08	0,92	0,00658
870	1010	940	4	67	3	0,04	0,96	0,00684
1010	1150	1080	1	69,5	0,5	0,01	0,99	0,00709

Строим график зависимости вероятности безотказной работы R(t) и вероятности отказа Q(t) по экспериментальным данным.

1,2

1

0,8


R(t), Q(t)
0,6

0,4

0,2

0

0 500 1000 1500