определение среднего времени безотказной работы. Методические указания составлены на основе Требований к разработке методических указаний для студентов по проведению лабораторных работ и практических занятий
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Время t, час Рисунок 5.3 – График зависимости вероятности безотказной работы и вероятности отказа от времени. Расчет числовых характеристик наработки до отказа. Средняя наработка до отказа определяется по формуле: t ni tiсер , N где ni– количество отказов изделий в рассматриваемом интервале; ti сер – середина рассматриваемого интервала. Таблица 5.5 – Промежуточные расчеты средней наработки до отказа
Дисперсия: n t2 12756800 Д i iсер t2 3482 61136 . N 70 t 247 0, 71. 348 Практическая работа №6 -7. Расчет количественных характеристик надежности при последовательном и параллельном, сложном соединении элементов Теоретические сведения Расчеты надежности - расчеты, предназначенные для определения количественных показателей надежности. Они проводятся на различных этапах разработки, создания и эксплуатации объектов. На этапе проектирования расчет надежности производится с целью прогнозирования (предсказания) ожидаемой надежности проектируемой системы. Такое прогнозирование необходимо для обоснования предполагаемого проекта, а также для решения организационно-технических вопросов: - выбора оптимального варианта структуры; - способа резервирования; - глубины и методов контроля; - количества запасных элементов; - периодичности профилактики. На этапе испытаний и эксплуатации расчеты надежности проводятся для оценки количественных показателей надежности. Такие расчеты носят, как правило, характер констатации. Результаты расчетов в этом случае показывают, какой надежностью обладали объекты, прошедшие испытания или используемые в некоторых условиях эксплуатации. На основании этих расчетов разрабатываются меры по повышению надежности, определяются слабые места объекта, даются оценки его надежности и влияния на нее отдельных факторов. Многочисленные цели расчетов привели к большому их разнообразию. На рис. 1 изображены основные виды расчетов. Элементный расчет - определение показателей надежности объекта, обусловленных надежностью его комплектующих частей (элементов). В результате такого расчета оценивается техническое состояние объекта (вероятность того, что объект будет находиться в работоспособном состоянии, средняя наработка на отказ и т.п.). 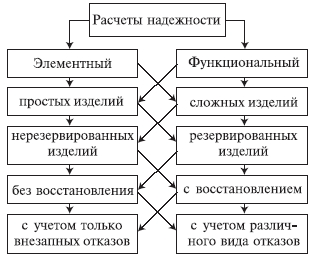 Рис.1. Классификация расчетов надежности Расчет функциональной надежности - определение показателей надежности выполнения заданных функций (например, вероятность того, что система очистки газа будет работать заданное время, в заданных режимах эксплуатации с сохранением всех необходимых параметров по показателям очистки). Поскольку такие показатели зависят от ряда действующих факторов, то, как правило, расчет функциональной надежности более сложен, чем элементный расчет. Выбирая на рис.1 варианты перемещений по пути, указанному стрелками, каждый раз получаем новый вид (случай) расчета. Самый простой расчет - расчет, характеристики которого представлены на рис. 4.5.1 слева: элементный расчет аппаратурной надежности простых изделий, нерезервированных, без учета восстановлений работоспособности при условии, что время работы до отказа подчинено экспоненциальному распределению. Самый сложный расчет - расчет, характеристики которого представлены на рис. 4.5.1 справа: функциональной надежности сложных резервированных систем с учетом восстановления их работоспособности и различных законов распределения времени работы и времени восстановления. Выбор того или иного вида расчета надежности определяется заданием на расчет надежности. На основании задания и последующего изучения работы устройства (по его техническому описанию) составляется алгоритм расчета надежности, т.е. последовательность этапов расчета и расчетные формулы. Последовательность расчета систем Последовательность расчета системы представлена на рис. 2. Рассмотрим основные ее этапы. 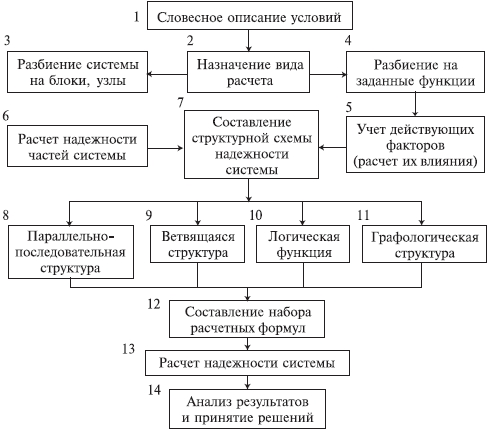 Рис. 2. Алгоритм расчета надежности Прежде всего четко следует сформулировать задание на расчет надежности. В нем должны быть указаны: 1) назначение системы ее состав и основные сведения о функционировании; 2) показатели надежности и признаки отказов, целевое назначение расчетов; 3) условия, в которых работает (или будет работать) система; 4) требования к точности и достоверности расчетов, к полноте учета действующих факторов. На основании изучения задания делается вывод о характере предстоящих расчетов. В случае расчета функциональной надежности осуществляется переход к этапам 4-5-7, в случае расчета элементов (аппаратурной надежности) - к этапам 3-6-7. Под структурной схемой надежности понимается наглядное представление (графическое или в виде логических выражений) условий, при которых работает или не работает исследуемый объект (система, устройство, технический комплекс и т.д.). Типовые структурные схемы представлены на рис. 3. 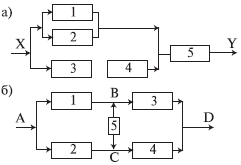 Рис. 3. Типовые структуры расчета надежности Простейшей формой структурной схемы надежности является параллельно-последовательная структура. На ней параллельно соединяются элементы, совместный отказ которых приводит к отказу В последовательную цепочку соединяются такие элементы, отказ любого из которых приводит к отказу объекта. На рис. 3,а представлен вариант параллельно-последовательной структуры. По этой структуре можно сделать следующее заключение. Объект состоит из пяти частей. Отказ объекта наступает тогда, когда откажет или элемент 5, или узел, состоящий из элементов 1-4. Узел может отказать тогда, когда одновременно откажет цепочка, состоящая из элементов 3,4 и узел, состоящий из элементов 1,2. Цепь 3-4 отказывает, если откажет хотя бы один из составляющих ее элементов, а узел 1,2 - если откажут оба элемента, т.е. элементы 1,2. Расчет надежности при наличии таких структур отличается наибольшей простотой и наглядностью. Однако не всегда удается условие работоспособности представить в виде простой параллельно-последовательной структуры. В таких случаях используют или логические функции, или графы и ветвящиеся структуры, по которым оставляются системы уравнений работоспособности. На основе структурной схемы надежности составляется набор расчетных формул. Для типовых случаев расчета используются формулы, приведенные в справочниках по расчетам надежности, стандартах и методических указаниях. Прежде чем применять эти формулы, необходимо предварительно внимательно изучить их существо и области использования. Расчет надежности, основанный на использовании параллельно-последовательных структур Пусть некоторая техническая система D составлена из n элементов (узлов). Допустим, надежности элементов нам известны. Возникает вопрос об определении надежности системы. Она зависит от того, каким образом элементы объединены в систему, какова функция каждого из них и в какой мере исправная работа каждого элемента необходима для работы системы в целом. Параллельно-последовательная структура надежности сложного изделия дает представление о связи между надежностью изделия и надежностью его элементов. Расчет надежности ведется последовательно - начиная от расчета элементарных узлов структуры к ее все более сложным узлам. Например, в структуре рис. 5.3,а узел, состоящий из элементов 1-2 - элементарный узел, состоящий из элементов 1-2-3-4, сложный. Эта структура может быть сведена к эквивалентной, состоящей из элементов 1-2-3-4 и элемента 5, соединенных последовательно. Расчет надежности в данном случае сводится к расчету отдельных участков схемы, состоящих из параллельно и последовательно соединенных элементов. Соединение элементов называется последовательным, если отказ хотя бы одного элемента приводит к отказу всей системы. Система последовательно соединенных элементов работоспособна тогда, когда работоспособны все ее элементы. Вероятность безотказной работы системы за время t определяется формулой где Рi(t) - вероятность безотказной работы i-го элемента за время t, n – количество элементов в системе. Если Рi (t) =Р(t), то Pc(t)=Pn(t). (2) Выразим Рс(t) через интенсивность отказов λi(t) элементов системы. Имеем: 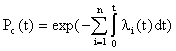 ( 3) ( 3)или  (4) (4)где Здесьλ i(t) - интенсивность отказов i-го элемента; λс(t) - интенсивность отказов системы. Вероятность отказа системы на интервале времени (0, t ) равна Частота отказов системы fc(t) определяется соотношением Интенсивность отказов системы Среднее время безотказной работы системы: 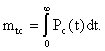 ( 9) ( 9)В случае экспоненциального закона надежности всех элементов системы имеем 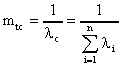 ; (16) ; (16)где mti - среднее время безотказной работы i - го элемента. Этот метод расчета надежности системы рекомендуется применять при окончательном расчете надежности, когда установлены экспериментально λ-характеристики для элементов системы. При ориентировочном расчете принимают следующие допущения: Известны интенсивности отказов λ элементов системы Известно число элементов в системе Однотипные элементы равнонадежны, т.е. имеют одинаковую интенсивность отказов, равную среднестатистическомй значению. Тогда показатели надежности рассчитываются по следующим формулам 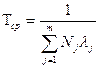 Решение типовых задач. Задача 3.1. Система состоит из трех блоков, среднее время безотказной работы которых равно : mt1=160 час; mt2 =320 час; mt3 = 600 час. Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднее время безотказной работы системы. Решение. Воспользовавшись формулой (17) получим Здесь λi - интенсивность отказов i -го блока. На основании формулы (11) имеем Здесь λc - интенсивность отказов системы. На основании формулы (17) получим: Задача 3.2. Система состоит из 12600 элементов, средняя интенсивность отказов которых λср=0,32*10-6 1/час. Справедлив экспоненциальный закон надежности. Требуется определить Pc(t), qc(t), fc(t), mtc, для t=50 час. Решение. Интенсивность отказов системы по формуле (11) будет λс = λср*n = 0,32*10-6*12600 = 4,032*10-3 1/час . Из (3.13) имеем Рс(t) = e-λct ; Рс(50) = e-4,032*0,001*50 0=0,82 . Из (3.15) получим qc(t)= 1- Pc(t) ; qc(50)=1-Pc(50)= 0,18 . Из (3.14) имеем fc(t) = λce-λct =λcPc(t); fc(50) = 4,032*10-3*0,82 = 3,28*10-3 1/час. Из (3.16) получим mtс=1/λc=1/4,032*10-3=250 час. Система с параллельным соединением элементов На рис. 4.5.6 представлено параллельное соединение элементов 1, 2, 3. Это означает, что устройство, состоящее из этих элементов, переходит в состояние отказа после отказа всех элементов при условии, что все элементы системы находятся под нагрузкой, а отказы элементов статистически независимы. 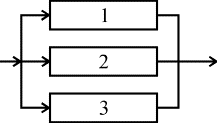 Рис.6. Блок-схема системы с параллельным соединением элементов Условие работоспособности устройства можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1 или элемент 2, или элемент 3, или элементы 1 и 2, 1; и 3, 2; и 3, 1; и 2; и 3. Вероятность безотказного состояния устройства, состоящего из n параллельно соединенных элементов определяется по теореме сложения вероятностей совместных случайных событий как Р=(р1+р2+...рn)-(р1р2+р1р3+...)-(р1р2р3+р1р2рn+...)-... ± (р1р2р3...рn). (7) Для приведенной блок-схемы (рис. 4.5.6), состоящей из трех элементов, выражение (7) можно записать: Р=р1+р2+р3-(р1р2+р1р3+р2р3)+р1р2р3. Применительно к проблемам надежности, по правилу умножения вероятностей независимых (в совокупности) событий, надежность устройства из n элементов вычисляется по формуле Р = 1- , (8) т.е. при параллельном соединении независимых (в смысле надежности) элементов их ненадежности (1-pi=qi) перемножаются. В частном случае, когда надежности всех элементов одинаковы, формула (4.5.8) принимает вид Р = 1 - (1-р)n. (9) Пример 4.5.5. Предохранительное устройство, обеспечивающее безопасность работы системы под давлением, состоит из трех дублирующих друг друга клапанов. Надежность каждого из них р=0,9. Клапаны независимы в смысле надежности. Найти надежность устройства. Решение. По формуле (9) Р=1-(1-0,9)3=0,999. Интенсивность отказов устройства состоящего из n параллельно соединенных элементов, обладающих постоянной интенсивностью отказов l0, определяется как  . (4.5.10) . (4.5.10)Из (4.5.10) видно, что интенсивность отказов устройства при n>1 зависит от t: при t=0 она равна нулю, при увеличении t, монотонно возрастает до l0. Если интенсивности отказов элементов постоянны и подчинены показательному закону распределения, то выражение (4.5.8) можно записать Р(t) = 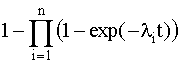 . (11) . (11)Среднее время безотказной работы системы Т0 находим, интегрируя уравнение (11) в интервале [0,¥]: Т0=  =(1/l1+1/l2+…+1/ln)-(1/(l1+l2)+ 1/(l1+l3)+…)+ (12) +(1/(l1+l2+l3)+1/(l1+l2+l4)+…)+(-1)n+1´ . В случае, когда интенсивности отказов всех элементов одинаковы, выражение (12) принимает вид Т0= . (13) Среднее время работы до отказа также можно получить, интегрируя уравнение (7) в интервале [0,¥] Пример 6. Предположим, что два одинаковых вентилятора в системе очистки отходящих газов работают параллельно, причем если один из них выходит из строя, то другой способен работать при полной системной нагрузке без изменения своих надежностных характеристик. Требуется найти безотказность системы в течение 400ч (продолжительность выполнения задания) при условии, что интенсивности отказов двигателей вентиляторов постоянны и равны l=0,0005ч-1, отказы двигателей статистически независимы и оба вентилятора начинают работать в момент времени t=0. Решение. В случае идентичных элементов формула (11) принимает вид Р(t) = 2еxp(-lt) - еxp(-2lt). Поскольку l = 0,0005 ч-1 и t = 400 ч, то Р(400) = 2еxp(-0,0005´400) - еxp(-2´0,0005´400)=0,9671. Среднюю наработку на отказ находим, используя (13): Т0= 1/l(1/1 + 1/2) = 1/l´3/2 = 1,5/0,0005 = 3000 ч. Способы преобразования сложных структур Относительная простота расчетов надежности, основанных на использовании параллельно-последовательных структур, делают их самыми распространенными в инженерной практике. Однако не всегда условие работоспособности можно непосредственно представить параллельно-последовательной структурой. В этом случае можно сложную структуру заменить ее эквивалентной параллельно-последовательной структурой. К таким преобразованиям относится: - преобразование с эквивалентной заменой треугольника на звезду и обратно; - разложение сложной структуры по базовому элементу. Существо способа преобразования с помощью эквивалентной замены треугольника на звезду и обратно заключается в том, что узел сложной конфигурации заменяется на узел другой, более простой конфигурации, но при этом подбираются такие характеристики нового узла, что надежности преобразуемой цепи сохранялись прежними. Пусть, например, требуется заменить треугольник (рис. 4.5.7,а) звездой (рис. 4.5.7,б) при условии, что вероятность отказа элемента a равна q13, элемента b равна q12, элемента c - q23. Переход к соединению звездой не должен изменить надежность цепей 1-2, 1-3, 2-3. Поэтому значение вероятностей отказов элементов звезды q1, q2, q3 должны удовлетворять следующим равенствам: 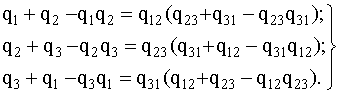 (14) (14)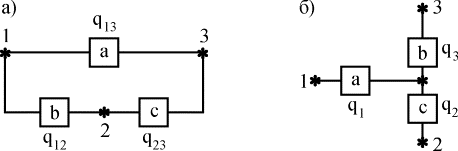 Рис.7. Преобразование "треугольник - звезда" Если пренебречь произведениями вида qiqj; qiqjqk, то в результате решения системы уравнения (4.5.14) можно записать: q1=q12q31; q2=q23q12; q3=q31q23. (15) Для обратного преобразования звезды в треугольник q12= ; q23= ; q31= . (16) Пример 7. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9, а вероятности отказов равны 0,1. Решение. 1. Преобразуем соединение элементов 1,2,5 в треугольник (рис.8,а), в звезду (рис. 8, б).  Рис. 8. К примеру преобразования структуры 2. Определим эквивалентные значения вероятности отказов для новых элементов a, b, c qa=q1q2=0,1´0,1 = 0,01; qb=q1q5=0,1´0,1 = 0,01; qс=q2q5=0,1´0,1 = 0,01. 3. Определим значения вероятности безотказного состояния элементов эквивалентной схемы (рис. 4.5.8,б) pa = pb = pc = 0,99. 4. Определим вероятность безотказной работы эквивалентного устройства (рис.9): Р = рa(рbр3 + рcр4 - рbр3рcр4) = = 0,99(0,99´0,9+0,99´0,9 - 0,99´0,9´0,99´0,9) = 0,978.  Рис. 9. Преобразованная структура Способ преобразования с помощью разложения сложной структуры по некоторому базовому элементу основан на использовании теоремы о сумме вероятностей несовместных событий. В сложной структуре выбирают базовый элемент (или группу базовых элементов) и делаются следующие допущения: - базовый элемент находится в работоспособном состоянии; - базовый элемент находится в отказавшем состоянии. Для этих случаев, представляющих собой два несовместных события, исходная структура преобразовывается в две новые схемы. В первой из них вместо базового элемента ставится "короткое замыкание" цепи, а во второй - разрыв. Вероятности безотказной работы каждой из полученных простых структур вычисляются и умножаются: первая - на вероятность безотказного состояния базового элемента, вторая - на вероятность отказа базового элемента. Полученные произведения складываются. Сумма равна искомой вероятности безотказной работы сложной структуры. Пример 8. Решить предыдущий пример методом разложения сложной структуры. Решение. 1. В качестве базового элемента примем элемент 5 (рис. 3,б). 2. Закоротим базовый элемент, т.е. сделаем допущение об абсолютной его проводимости. Присоединим к полученной структуре последовательно базовый элемент с характеристикой его надежности р5. В результате вместо исходной структуры получим новую структуру (рис. 10,а). 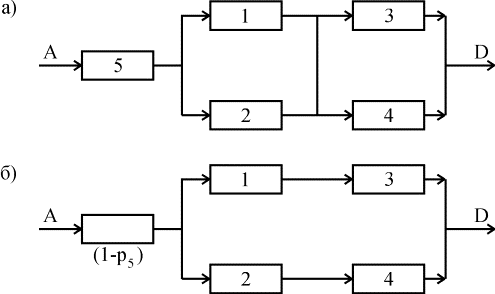 Рис. 10. Пример разложения мостиковой структуры по базовому элементу 3. Произведем обрыв базового элемента, т.е. сделаем предположение об его абсолютной ненадежности (непроводимости). К полученной структуре присоединим последовательно базовый элемент с характеристикой его ненадежности (1-р5). В результате получим структуру (рис. 10,б). 4. Искомая вероятность равна сумме вероятностей структур (рис. 10,а,б), каждая из которых параллельно-последовательная. Поэтому Р = р5[(р1+р2-р1р2)(р3+р4-р3р4)] + (1-р5)[р1р3+р2р4-р1р3р2р4]= = 0,9[(0,9+0,9 - 0,9´0,9) ´ (0,9+0,9 - 0,9´0,9)] + + (1-0,9) ´ [0,9´0,9 + 0,9´0,9 - 0,9´0,9´0,9´0,9]»0,978. Вероятность безотказной работы мостиковой схемы, состоящей из пяти неодинаковых и независимых элементов, можно определить по формуле: Р=2р1р2р3р4р5-р2р3р4р5-р1р3р4р5-р1р2р4р5-р1р2р3р5- -р1р2р3р4+р1р3р5+р2р3р4+р1р4+р2р5. (17) В случае идентичных элементов эта формула принимает вид Р = 2р5-5р4+2р3+2р2. (18) Подставляя соотношение (18) в формулу (4), получаем, что в случае использования элементов с постоянной интенсивностью отказов (экспоненциальном законе распределения отказов) Р(t) = 2ехр(-5lt)-5ехр(-4lt)+2ехр(-3lt)+2ехр(-2lt). (19) Среднее время безотказной работы системы Т0 находим, путем интегрирования уравнения (5.19) в интервале [0,¥]: Т0 = 2ехр(-5lt)-5ехр(-4lt)+2ехр(-3lt)+2ехр(-2lt)dt= = (49/60)´(1/l). (20) Пример 9. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 3,б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9. Решение. Так как все элементы идентичны, воспользуемся формулой (18); с ее помощью получаем: Р = 2´0,95 - 5´0,94+2´0,93 + 2´0,92»0,978. Пример 4.5.10. Требуется определить вероятность безотказной работы и среднюю наработку на отказ системы, состоящей из пяти независимых и одинаковых элементов, соединенных по мостиковой схеме (рис. 4.5.3,б); считается, что l=0,0005ч-1, t=100ч и все элементы начинают работать в момент времени t=0. Решение. 1. С помощью формулы (4.5.19) получаем Р(100) = 2е-0,25-5е-0,2+2е-0,15+2е-0,1 = 0,9999. 2. Подставляя полученное значение вероятности безотказной работы в формулу (20), находим среднюю наработку на отказ Т0 = 49/(60´0,0005) = 1633,4 ч. Надежность резервированной системы Одним из путей повышения надежности системы является введение в нее резервных (дублирующих) элементов. Резервные элементы включаются в систему как бы "параллельно" тем, надежность которых недостаточна. Параллельное соединение резервного оборудования системы Рассмотрим самый простой пример резервированной системы - параллельное соединение резервного оборудования системы. В этой схеме все n одинаковых образцов оборудования работают одновременно, и каждый образец оборудования имеет одинаковую интенсивность отказов. Такая картина наблюдается, например, если все образцы оборудования держатся под рабочим напряжением (так называемый "горячий резерв"), а для исправной работы системы должен быть исправен хотя бы один из n образцов оборудования. В этом варианте резервирования применимо правило определения надежности параллельно соединенных независимых элементов. В нашем случае, когда надежности всех элементов одинаковы, надежность блока определяется по формуле (9) Р = 1 - (1-р)n. Если система состоит из n образцов резервного оборудования с различными интенсивностями отказов, то P(t) = 1-(1-p1) (1-p2)... (1-pn). (21) Выражение (4.5.21) представляется как биноминальное распределение. Поэтому ясно, что когда для работы системы требуется по меньшей мере k исправных из n образцов оборудования, то P(t) = pi(1-p)n-i, где  . (22) . (22)При постоянной интенсивности отказов l элементов это выражение принимает вид P(t) =  , (22.1) , (22.1)где р = еxp(-lt). Варианты задач для самостоятельного решения 1. На фирме имеется 230 компьютеров. В течении года вышли из строя и были заменены 3 винчестера, 10 вентиляторов для охлаждения процессора, 1 материнская плата, 2 видеокарты, 4 сетевые карты, 2 блока питания и 1 монитор. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 2. На фирме имеется 180 компьютеров. В течении года вышли из строя и были заменены 4 винчестера, 3 вентилятора для охлаждения процессора, 2 материнские платы, 1 видеокарта, 7 сетевых карты, 1 блок питания и 2 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 3. На фирме имеется 340 компьютеров. В течении года вышли из строя и были заменены 10 винчестеров, 17 вентиляторов для охлаждения процессора, 3 материнских платы, 2 видеокарты, 3 сетевые карты, 5 блоков питания и 3 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 4. На фирме имеется 270 компьютеров. В течении года вышли из строя и были заменены 4 винчестера, 9 вентиляторов для охлаждения процессора, 2 материнских платы, 4 видеокарты, 30 сетевых карты, 4 блока питания и 2 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 5. На фирме имеется 470 компьютеров. В течении года вышли из строя и были заменены 2 винчестера, 78 вентиляторов для охлаждения процессора, 3 материнских платы, 14 видеокарт, 7 сетевых карты, 7 блоков питания и 23 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 6. На фирме имеется 160 компьютеров. В течении 2 лет вышли из строя и были заменены 4 винчестера, 9 вентиляторов для охлаждения процессора, 2 материнских платы, 4 видеокарты, 13 сетевых карты, 3 блока питания и 4 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциональный (нормальный участок эксплуатации). 7. На фирме имеется 920 компьютеров. В течении года вышли из строя и были заменены 12 винчестеров, 37 вентиляторов для охлаждения процессора, 7 материнских платы, 9 видеокарты, 20 сетевых карты, 8 блоков питания и 21 монитор. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 8. На фирме имеется 760 компьютеров. В течении года вышли из строя и были заменены 14 винчестеров, 19 вентиляторов для охлаждения процессора, 6 материнских платы, 3 видеокарты, 56 сетевых карты, 23 блока питания и 17 мониторов. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 9. На фирме имеется 260 компьютеров. В течении года вышли из строя и были заменены 2 винчестера, 7 вентиляторов для охлаждения процессора, 2 материнских платы, 4 видеокарты, 13 сетевых карты, 3 блока питания и 2 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 10. На фирме имеется 540 компьютеров. В течении года вышли из строя и были заменены 4 винчестера, 19 вентиляторов для охлаждения процессора, 5 материнских платы, 3 видеокарты, 24 сетевых карты, 6 блока питания и 7 мониторов. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 11. На фирме имеется 680 компьютеров. В течении года вышли из строя и были заменены 10 винчестеров, 32 вентилятора для охлаждения процессора, 5 материнских платы, 8 видеокарты, 43 сетевых карты, 15 блоков питания и 21 монитор. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 12. На фирме имеется 850 компьютеров. В течении 3 лет вышли из строя и были заменены 46 винчестеров, 94 вентилятора для охлаждения процессора, 23 материнских платы, 47 видеокарты, 78 сетевых карты, 27 блока питания и 36 мониторов. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 13. На фирме имеется 780 компьютеров. В течении года вышли из строя и были заменены 10 винчестеров, 21 вентилятор для охлаждения процессора, 6 материнских платы, 14 видеокарты, 36 сетевых карты, 36 блока питания и 43 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 14. На фирме имеется 230 компьютеров. В течении года вышли из строя и были заменены 3 винчестера, 10 вентиляторов для охлаждения процессора, 1 материнская плата, 2 видеокарты, 4 сетевые карты, 2 блока питания и 1 монитор. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (участок эксплуатации характеризуется коэффициентами Кэ=1.033). 15. На фирме имеется 180 компьютеров. В течении года вышли из строя и были заменены 4 винчестера, 3 вентилятора для охлаждения процессора, 2 материнские платы, 1 видеокарта, 7 сетевых карты, 1 блок питания и 2 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (учесть цикличность работы ПЭВМ). 16. На фирме имеется 340 компьютеров. В течении года вышли из строя и были заменены 10 винчестеров, 17 вентиляторов для охлаждения процессора, 3 материнских платы, 2 видеокарты, 3 сетевые карты, 5 блоков питания и 3 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (участок эксплуатации характеризуется коэффициентами Ксл=1.066). 17. На фирме имеется 270 компьютеров. В течении года вышли из строя и были заменены 4 винчестера, 9 вентиляторов для охлаждения процессора, 2 материнских платы, 4 видеокарты, 30 сетевых карты, 4 блока питания и 2 монитора. Определить вероятность безотказной работы компьютера в течении 3-х лет, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (учесть цикличность работы ПЭВМ). 18. На фирме имеется 470 компьютеров. В течении года вышли из строя и были заменены 2 винчестера, 78 вентиляторов для охлаждения процессора, 3 материнских платы, 14 видеокарт, 7 сетевых карты, 7 блоков питания и 23 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 19. На фирме имеется 160 компьютеров. В течении 2 лет вышли из строя и были заменены 4 винчестера, 9 вентиляторов для охлаждения процессора, 2 материнских платы, 4 видеокарты, 13 сетевых карты, 3 блока питания и 4 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (участок эксплуатации характеризуется коэффициентами Кэ=1,027). 20. На фирме имеется 920 компьютеров. В течении года вышли из строя и были заменены 12 винчестеров, 37 вентиляторов для охлаждения процессора, 7 материнских платы, 9 видеокарты, 20 сетевых карты, 8 блоков питания и 21 монитор. Определить вероятность безотказной работы компьютера в течении месяца, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (учесть цикличность работы ПЭВМ, принять интенсивность отказа на один цикл λц=10-5 1/ч). 21. На фирме имеется 760 компьютеров. В течении года вышли из строя и были заменены 14 винчестеров, 19 вентиляторов для охлаждения процессора, 6 материнских платы, 3 видеокарты, 56 сетевых карты, 23 блока питания и 17 мониторов. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (нормальный участок эксплуатации). 22. На фирме имеется 260 компьютеров. В течении года вышли из строя и были заменены 2 винчестера, 7 вентиляторов для охлаждения процессора, 2 материнских платы, 4 видеокарты, 13 сетевых карты, 3 блока питания и 2 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (участок эксплуатации характеризуется коэффициентами Ксл=1,057). 23. На фирме имеется 780 компьютеров (из них 10 серверов работают круглосуточно). В течении года вышли из строя и были заменены 10 винчестеров, 21 вентилятор для охлаждения процессора, 6 материнских платы, 14 видеокарты, 36 сетевых карты, 36 блока питания и 43 монитора. Определить вероятность безотказной работы компьютера в течении года, если принять, что закон распределения вероятностей отказа комплектующих – экспоненциальный (учесть цикличность работы ПЭВМ, принять интенсивность отказа на один цикл λц=10-5 1/ч). | ||||||||||||||||||||||||||||||||||||||||
