определение среднего времени безотказной работы. Методические указания составлены на основе Требований к разработке методических указаний для студентов по проведению лабораторных работ и практических занятий

• Название: Методические указания составлены на основе Требований к разработке методических указаний для студентов по проведению лабораторных работ и практических занятий
• Анкор: определение среднего времени безотказной работы
• Дата: 15.12.2021
• Размер: 0.74 Mb.
• Имя файла: 00140318-120ab073.docx
• Тип: Методические указания; #305158
• страница: 6 из 9

Практическая работа №8

«Расчет количественных характеристик надежности при постоянном резервировании.»

Цель: научить студентов определять показатели надежности объектов, представляющих сложные системы.

Задачи обучения:

• 
  ознакомить с методами резервирования;
  
• 
  привить навыки построения структуры сложной системы;
  
• 
  научить рассчитывать показатели надежности системы без резервирования;
  
• 
  научить рассчитывать показатели надежности системы с резервированием.
  

Методы и формы обучения и преподавания: индивидуальная работа, работа в парах; ситуационные задачи, выполнение домашних заданий.

Материально- техническое оснащение:

Калькулятор или компьютер с программами EXCEL или MathCAD.

Задания и методические указания к их выполнению (алгоритм, форма, сроки отчетности, критерии оценивания):

Пример 1. Определить вероятность безотказной работы и вероятность отказа основной системы, состоящей из пяти элементов, если вероятности безотказной работы элементов равны P₁(t)=0,98, P₂(t)=0,97, P₃(t)=0,99, P₄(t)=0,98, P₅(t)=0,96.

Решение: вероятность безотказной работы системы P_с(t) определяем по формуле (1):

P_ct  P₁ t P₂ t... P₅ t  0,980,970,990,980,96  0,885, вероятность отказа Q_c(t) системы определяется по формуле (5):

Q_c t  1 P_c t  1 0,885  0,115.

Ответ: P_c t  0,885 Q_c  0,115.

Пример 2. Определить среднее время безотказной работы системы, если система состоит из трех элементов, среднее время безотказной работы которых равны 400, 200 и 500 часов, закон распределения – экспоненциальный.

Решение: Определим интенсивности отказов элементов по формуле (11)

₁ 

₃ 

1 _ 1

T₁ 400

1 _ 1

T₃ 500

 0,0025 1/час;

 0,0021/час.

₂ 


1

T
2

_ 1

200

 0,0051/час;

Интенсивность отказа системы определяем по формуле (7)

_c  ₁  ₂  ₃  0,0025 0,005 0,002  0,0095 1/час.

Наработку до отказа системы рассчитаем по формуле (8)


T ¹ 



1

0,0095

 105,3 час.

Ответ: T  105,3 час.

Пример 3. Система состоит из трех элементов, вероятность безотказной работы которых в течении 100 часов равны Р₁(100) = 0,95; Р₁(100) = 0,99; Р₃(100) = 0,97. Найти среднее время безотказной работы системы, закон распределения – экспоненциальный.

Решение: Определим вероятность безотказной работы системы

P(100)  P₁ 100P₂ 100P₃ 100  0,95 0,99 0,97  0,912.

Выразим интенсивность отказа системы из формулы (6)

_{  } lnPt_{ } ln 0,912 _{ 0,0092.}

t 100

Среднее время безотказной работы системы определяем по формуле (8)


T ¹ 



1

0,0092

 1085,6

час.

Ответ: T  1085,6 час.

Пример 4. Система состоит из 6000 элементов, средняя интенсивность отказов которых

_ср=5,4*10^-7 1/час. Определить вероятность безотказной работы, вероятность отказа, плотность вероятности времени безотказной работы за время 100 часов, и среднее время безотказной работы.

Решение: Интенсивность отказов системы определяем по формуле (7)

n

  __i

i1

 n_cp

 6000 5,4 10^7  3,24 10^3 .

Вероятность безотказной работы рассчитаем по формуле (6)

_n

Pt  _e^it

i1

_{ e}t

_{ e}0,00324100 _{ 0,72,}

Вероятность отказа системы

Qt   1  Pt   1  0,72  0,28

Наработка до отказа системы


T ¹ 



1

3,24 10^3

 308,6 час.

3 _3
Плотность вероятности времени безотказной работы

ft    e^t

 3,24 10^3  e^{3,2410 100}  2,3 10 1/час.

Пример 6. Система состоит из трех элементов с равной вероятностью безотказной работы равной 0,9. Определить вероятности безотказной работы системы при различных вариантах резервирования.

Решение: а) расчет показателей надежности системы без резервирования:

Вероятность безотказной работы системы без резервирования определяется по формуле (2.1):

P t  P³ t  0,9³  0,729 ,

c i

Вероятность отказа системы без резервирования определяем по формуле (5)


n
Q t   1  _ P t   1  0,9³  1  0,729  0,271.

c i

i1

б) расчет показателей надежности системы при общем резервировании:

Структурная схема системы с общим резервированием показана на рисунке 3.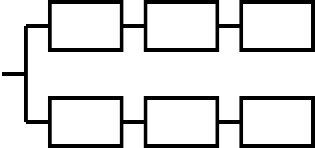




^P11 ^P12 ^P13

^P21 ^P22 ^P23

Рисунок 1 – Схема системы с общим резервирование:

Р₁₁, Р₁₂, Р₁₃ – вероятности безотказной работы элементов основной системы; Р₂₁, Р₂₂, Р₂₃ – вероятности безотказной работы элементов резервной системы

(6):

Вероятность отказа системы с общим резервированием определяется по формуле

Q_c t  Q_OC t Q_PC t,

где Q_OC(t) – вероятность отказа основной системы;

Q_PC(t) – вероятность отказа резервной системы.

Вероятность отказа основной системы определяем по формуле (5)

n

^QOC

t   1  _ P t   1  0,9³  1  0,729  0,271.


i
i1

Вероятность отказа резервной системы равна

n

^QPC

t   1  _ P t   1  0,9³  1  0,729  0,271.


i
i1

Вероятность отказа системы:

Q_c t  Q_OC t Q_PC t  0,271 0,271 0,073.

Вероятность безотказной системы с общим резервированием определяем по формуле (2.8)

P_c t  1 Q_c t  1 0,073  0,927.

в) расчет показателей надежности системы при поэлементном резервировании: Структурная схема системы с поэлементным резервированием показана на рисунке

2.

^P11 ^P12 ^P13

^P21 ^P22 ^P23

Рисунок 2 – Схема системы с поэлементным резервирование: Р₁₁, Р₁₂, Р₁₃ – вероятности безотказной работы основных элементов; Р₂₁, Р₂₂, Р₂₃ – вероятности безотказной работы резервных элементов

Вероятность безотказной работы системы с поэлементным резервированием определяем по формуле (2.6):

P_c t  P_1121 t P_1222 t P_1323 t,

где Р_11-21(t) – вероятность безотказной работы группы из первого основного и резервного элементов;

Р_12-22(t) – вероятность безотказной работы группы из второго основного и резервного элементов;

Р_13-23(t) – вероятность безотказной работы группы из третьего основного и резервного элементов.

P_1121 t  1  1  P₁₁ t 1  P₂₁ t  1  (1  0,9)  1  0,9  1  0,01  0,99 P_1222 t  1  1  P₁₂ t 1  P₂₂ t  1  (1  0,9)  1  0,9  1  0,01  0,99 P_1323 t  1 1 P₁₃ t 1 P₂₃ t  1 (1 0,9)  1 0,9  1 0,01  0,99

Вероятность безотказной работы системы с поэлементным резервированием:

P_c t  P_1121 t P_1222 t P_1323 t  0,99 0,99 0,99  0,97,

Так как вероятности безотказной работы групп элементов близки к единице, можно было воспользоваться формулой для приближенного расчета (3):

n 3

P_c t   1  _1  P_i t   1  _1  0,99  1  0,03  0,97 .

i1 i1

Вероятность отказа основной системы определяем по формуле (5)

Q_c t  1 P_c t  1 0,97  0,03.

Ответ: для системы без резервирования: P_c t  0,729, Q_c t  0,271; для системы с общим

резервированием P_ct  0,927, Q_ct  0,073; для системы с поэлементным

резервированием: P_ct  0,97, Q_ct  0,03. Таким образом, максимальная надежность

достигается при поэлементном резервировании.

Задания для самостоятельной работы студентов

Задача 8.1. Определить вероятность безотказной работы системы, состоящей из 500 элементов, если вероятность безотказной работы каждого элемента в течение времени tравна P(t) = 0,998.

Задача 8.2. Вероятность безотказной работы системы, состоящей из 150 равнонадежных элементов, в течение времени t равна Р_c(t)=0,95. Найти вероятность безотказной работы элемента.

Задача 8.3. Блок управления состоит из 5000 элементов, средняя интенсивность отказов которых равна 2,3·10^-6 1/час. Определить вероятность безотказной работы в течении t = 100 час и среднее время безотказной работы.

Задача 8.4. Система состоит из пяти элементов, среднее время безотказной работы которых равно: Т₁=104 час; Т₂=200 час; Т₃=185 час; Т₄=350 час; Т₅=620 час. Показатели распределены по экспоненциальному закону. Определить среднее время безотказной работы системы.

Задача 8.5. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени t = 50 час равна: P₁(50)=0,98; P₂(50)=0,99; P₃(50)=0,998; P₄(50)=0,975; P₅(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднее время безотказной работы прибора.

Задача 8.6. Установка состоит из 3000 элементов, средняя интенсивность отказов которых 3,8·10^-6 1/час. Определить вероятность отказа установки в течении t = 300 час и среднее время безотказной работы аппаратуры.

Задача 8.7. Объект состоит из 200000 элементов, средняя интенсивность отказов которых 0,2·10^-6 1/час. Определить вероятность безотказной работы системы в течение 240 часов и среднее время безотказной работы.

Задача 8.8. Прибор состоит из 5 узлов. Надежность узлов характеризуется вероятностью безотказной работы в течение времени t , которая равна: P₁(t)=0,98; P₂(t)=0,99; P₃(t)=0,998; P₄(t)=0,975; P₅(t)=0,985. Необходимо определить вероятность безотказной работы прибора.

Задача 8.9. Определить количество равнонадежных резервных элементов с вероятностью безотказной работы P_i(t)=0,9,необходимых для того, чтобы обеспечить вероятность безотказной работы системы равную P_с(t)=0,99.

Задача 8.10. Система состоит из четырех элементов, имеющих интенсивность отказов равную λ₁ = 2,7·10^-7 1/час, λ₂ = 3,2·10^-7 1/час, λ₃ = 2,1·10^-7 1/час, λ₄ = 4,3·10^-7 1/час. Изобразить структурную схему системы и определить вероятность безотказной работы и вероятность отказа в течение 60 часов при общем резервировании системы.

Задача 8.11. Система состоит из четырех элементов, имеющих интенсивность отказов равную λ₁ = 2,7·10^-7 1/час, λ₂ = 3,2·10^-7 1/час, λ₃ = 2,1·10^-7 1/час, λ₄ = 4,3·10^-7 1/час. Изобразить структурную схему системы и определить вероятность безотказной работы и вероятность отказа в течение 60 часов при поэлементном резервировании системы.

Задача 8.12. Система состоит из одного элемента с вероятностью безотказной работы равной 0,93, резервный элемент имеет вероятность безотказной работы 0,95. Определить вероятность безотказной работы системы после замещения основного элемента резервным, сделать вывод.

Задача 8.13. Система состоит из трех элементов с вероятностью безотказной работы равной P₁(t)=0,9, P₂(t)=0,92, P_i(t)=0,87. Определить вероятности безотказной работы системы при различных вариантах резервирования.

Задача 8.14. Определить количество резервных элементов с вероятностью отказа равной 0,05, для того, чтобы вероятность безотказной работы системы была равна P_с(t)=0,999.

Задача 8.15 Система состоит из трех элементов с вероятностью безотказной работы равной P₁(t)=0,9, P₂(t)=0,92, P₃(t)=0,87. Определить время безотказной работы системы при общем резервировании.

Задача 8.16 Система состоит из трех элементов с вероятностью безотказной работы равной P₁(t)=0,9, P₂(t)=0,92, P₃(t)=0,87. Определить время безотказной работы системы при поэлементном резервировании.