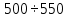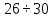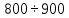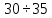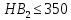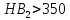практические. методичка по ТМ. Методическое пособие по выполнению практических заданий учебной дисциплины Техническая механика
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
|
ТЕМА: Зубчатые передачи. НАИМЕНОВАНИЕ РАБОТЫ: Расчет косозубой цилиндрической передачи. Цель работы: -Ознакомиться с назначением и видами редукторов. - Ознакомиться с конструкцией и назначением деталей передачи. -Рассчитать закрытую косозубую передачу одноступенчатого цилиндрического редуктора. - Углубить, систематизировать, обобщить теоретические знания по теме. Задание:Рассчитать закрытую косозубую передачу одноступенчатого цилиндрического редуктора привода винтового транспортера. Таблица№18
Таблица№19. Варианты заданий
ХОД РАБОТЫ Изучить назначение и виды редукторов (приложение № 1). Ознакомиться с чертежами редуктора и зубчатой передачи. Вычертить схему привода (приложение № 2). Произвести расчет закрытой косозубой передачи одноступенчатого цилиндрического редуктора. (согласно варианта). Оформить отчёт. НОРМА ВРЕМЕНИ: 4 часа МЕСТО ПРОВЕДЕНИЯ: учебный кабинет «Техническая механика». ОСНАЩЕНИЕ РАБОЧЕГО МЕСТА: • Инструкционная карта. • Калькулятор. • Чертежные принадлежности. ЛИТЕРАТУРА: 1. А.А. Эрдеди «Детали машин»- М.: Издательский центр «Академия», 2003.- стр.134-143. 2.В.П.Олофинская «Детали машин» краткий курс и тестовые задания- М: ФОРУМ,2010.- стр.27-32. ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА Общее передаточное отношение привода: iобщ= ωдв/ωт = угловая скорость колеса редуктора ω2 = ω1 / i = ωдв/iред= Вращающий момент на валу шестерни Т1= Ν1 / ω1 = Νдв/ωдв= Материал шестерни и колеса, размеры заготовок (приложение № 3) Рекомендуется твердость материала шестерни косозубой передачи выбирать возможно выше, для чего подвергать шестерню азотированию, цементации или поверхностной закалке. Применение высокотвердой шестерни повышает контактную прочность косозубой передачи. (Твердость зубьев вкосозубой шестерни должна быть выше, чем у колеса.) Выбор коэффициента долговечности. КНL= КFL = КНL — коэффициент долговечности, учитывающий влияние срока службы и режима нагрузки передачи КНLmax ≥ КНL ≥ 1. Для нормализованных или улучшенных колес КНLmax = 2,6; для колес с поверхностной закалкой, азотированием, цементацией КНLmax =1,8. КFL — коэффициент долговечности. При НВ ≤ 350 2 ≥ КFL ≥ 1. При НВ > 350 1,6 ≥ КFL ≥ 1. Рассчитываем пределы контактной выносливости (приложение 4) бно. Для материала шестерниб но1= Для материала колеса б но2= Рассчитываем пределы изгибной выносливости (приложение 5) бно. Для материала шестерниб Fо1 = Для материала колеса б Fо2 = а) Рассчитаем допустимые контактные напряжения Для материала шестерни[ б ] н2 = бно1 · КнL/Sн= Sн — требуемый коэффициент безопасности: Sн≈1,1÷1,2 (нижнее значение при нормализации, улучшении или объемной закалке). Для передач, выход из строя которых связан с тяжелыми последствиями, значения Sнувеличивают на ≈ 15%. Для материала колеса [ б ] н1 = бно2 · КнL/Sн= Для косозубной передачи условное допускаемое контактное напряжение [б]н= 0,45 ([б]н1 + [б]н2) = Должно соблюдаться условие [б]н ≤ 1,23 [б]н2 (сделать вывод на соблюдение данного условия). б) Рассчитаем допустимые напряжения изгиба Для материала шестерни [б]F1 = бF01 · КFL/SF = SF - требуемый коэффициент безопасности; SF ≈ 1,8 ÷ 2,3 (верхнее значение для литых колес) Для материала колес [б]F2 = бF02 · КFL/SF = Назначаем расчетные коэффициенты: Ψвd — коэффициент ширины венца колеса, зависящий от диаметра шестерни Ψвd= в2/d1 (приложение 6). Ψвd= Ψва - коэффициент ширины венца колеса, зависящий от межосевого расстояния передачи Ψва = в2/аw Ψва= 2 Ψвd/(i+1) = Значение Ψва корректируем по стандартному ряду: по ГОСТ 2185-66 Ψва = 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1; 1,25. Кнβ — коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по длине контактных линии (приложение 7).Кнβ = Рассчитываем межосевое расстояние передачи = Значение αw — корректируем по стандартному ряду: по ГОСТ СТСЭВ 229-75 αw = 40; 50; 63; 80; 100; 125; 160; 200; 250; 315; 400; 500; 630; 800; 1000; 1250; 1600; 2000 мм. Нормальный модуль зубьев. Задаются модулем зубьев m. Для передач общего назначения при улучшенных сталях рекомендуется m = (0,01-0,02) αw, а при закаленных — m = (0,016 -0,031) αw. Принимать m< 2 мм в силовых передачах не рекомендуется. Уменьшение модуля зацепления m и соответствующее увеличение числа зубьев Z способствует уменьшению удельного скольжения, что увеличивает надежность против заедания. mn= (0,01 — 0,02) αw = По ГОСТ 9563-60 (приложение 11) принимаем mn= а) Задаемся предварительно углом наклона зуба β = Осевая сила Fа дополнительно нагружает подшипники, возрастая с увеличением β. По этой причине для косозубых колес принимают β = 8-180. Наличие в зацеплении осевых сил является недостатком косозубой передачи. б) Суммарное число зубьев ZΣ = (2αω cosβ)/ mn= в) Числа зубьев: шестерни Z1 = ZΣ / (ί + 1) = принимаем Z1 = ; колеса Z2 = ZΣ - Z1 = г) Фактический угол наклона зубьев cosβ = mnZΣ / 2αω = β = Передаточное число u = Z2 / Z1 = Основные геометрические размеры шестерни и колеса: диаметры делительных окружностей: d1 = mnZ1 / cosβ = d2 = mnZ2 / cosβ = при этом соблюдается равенство άω= αw = dα1 = d2 // 2 = Диаметры окружностей вершин: dα1 = d1 +2 mn= dα2 = d2 +2 mn= что соответствует предварительно принятым диаметрам заготовок; ширина венца: колесаb2 = ψαάω= шестерни b1 = b2 + 5мм = Окружная скорость косозубых колес υ = ω1 d1 / 2 = По (приложение 8) для уменьшения динамической нагрузки принимаем 8-ю степень точности изготовления зубчатых колес. Окружная сила Ft= 2Т1 / d1 = Принимаем расчетные коэффициенты: Кнα = Кнυ= КFβ = КFυ= Кнα — коэффициент, учитывающий распределение нагрузки между зубьями. Для косозубых колес при υ ≤ 15 м/с для 6-8-й степеней точности Кнα = ;Кнβ — коэффициент неравномерности нагрузки по ширине венца (приложение 7); Кнυ— коэффициент динамической нагрузки. Для косозубых передач рекомендуется: Кнυ= 1 — при любой твердости зубьев и υ ≤ 10 с/м; Кнυ= 1,2 — при твердости зубьев ≤ НВ350 и υ = 10-20 м/с; Кнυ= 1,1 — при твердости зубьев > НВ350 и υ = 10-20 м/с. Расчетное контактное напряжение = Условие прочности бн< [ б ] ]н т. е. условие прочности. Эквивалентные числа зубьев шестерни и колеса Ζυ1 = Ζ1 /cos3 β = 26/cos3 90 04' = 27 Ζυ2 = Ζ2 /cos3 β = 132/cos3 90 04' = 137 Коэффициенты формы зубьев (приложение 10) шестерни YF1 = ; колеса YF2 = . Сравнительная характеристика прочности зубьев на изгиб; шестерни[ б ]F1 / YF1 = колеса[ б ]F2 / YF2 = Проверочный расчет передачи на прочность необходимо вести по колесу, зубья которого менее прочны на изгиб. Расчетные напряжения изгиба в зубьях колеса бF2 = 0,9YF2 КFβКFυ = Условие прочности б F2<[ б ]F2 Вывод: ПРИЛОЖЕНИЯ к практической работе №1 по дисциплине «Детали машин» ПРИЛОЖЕНИЕ №1. Редуктором называется – механизм, понижающий угловую скорость в приводах от двигателя к рабочей машине. Редукторы состоят из зубчатых или червячных передач, установленных в отдельном корпусе. Редукторы широко применяются в различных отраслях машиностроения и поэтому они весьма разнообразны по кинематике и конструктивному исполнению. Редукторы бывают с цилиндрическими и коническими зубчатыми колесами, а также червячными парами. Зубчатые колеса могут быть с прямыми, косыми, круговыми и шевронными зубьями. Различают следующие виды редукторов: по типу передачи – цилиндрические конические червячные конически-цилиндрические червячно-цилиндрические по числу ступеней – одно, - двух, - трехступенчатые по расположению валов и зубчатых колес – горизонтальные, вертикальные Цилиндрические зубчатые редукторы благодаря широкому диапазону передаваемых мощностей, долговечности, простоте изготовления и обслуживания имеют широкое распространение. Одноступенчатые редукторы имеют передаточное число U 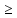 6,3 6,3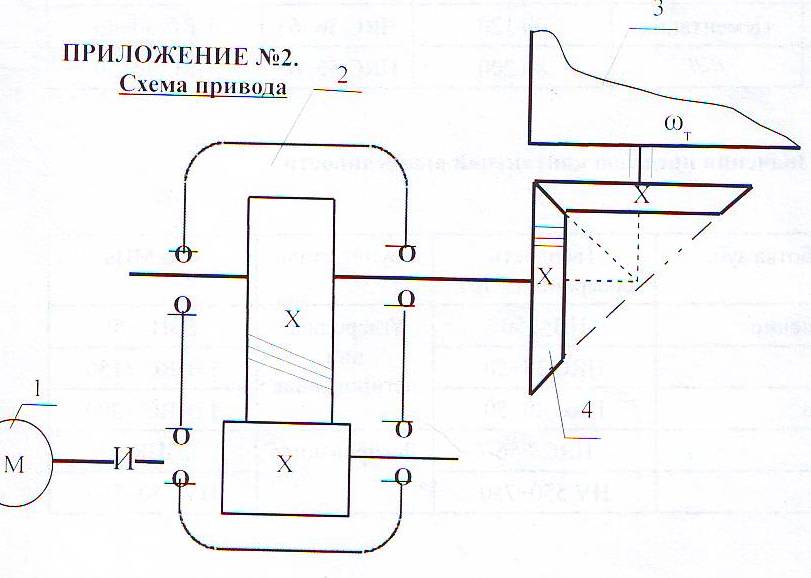 Электродвигатель Редуктор Винтовой транспортер Открытая коническая прямозубая передача ПРИЛОЖЕНИЕ №3. Механические характеристики сталей для зубчатых колес
ПРИЛОЖЕНИЕ №4. Значения пределов контактной выносливости
ПРИЛОЖЕНИЕ №5.Значения пределов изгибной выносливости
ПРИЛОЖЕНИЕ №6. Рекомендуемые значения Ψвd
*Большие значения при постоянной нагрузке ПРИЛОЖЕНИЕ №8. Степень точности передачи в зависимости от окружности скорости колес
ПРИЛОЖЕНИЕ №9. Ориентировочные значения коэффициента κFβ
ПРИЛОЖЕНИЕ№10. Значение коэффициента формы зуба YF для некоррегированного внешнего зацепления
ПРИЛОЖЕНИЕ №11. Модули зубьев m по ГОСТ 9563-60
ПРАКТИЧЕСКАЯ РАБОТА № 13 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 80 мм)
80 мм)