Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти

• Название: Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
• Дата: 10.06.2022
• Размер: 3.77 Mb.
• Имя файла: Mt_ЕММ_lab_MK.docx
• Тип: Методичні вказівки; #583697
• страница: 13 из 14

ТзОВ "Ролада" пропонує на ринок до 10 моделей одягу.

Згідно варіанту (табл. 11.2) необхідно:
Таблиця 11.2

Варіанти для виконання роботи

Варіант	Моделі одягу	Варіант	Моделі одягу
1	А-21, А-43, А-55, В-12, В-22, Д-25, Д-32, Д-37, Д-42, І-06	18	А-55, В-12, В-22, Д-25, Д-32, К-19, Л-23, Л-29, Л-30, Л-41
2	А-21, А-43, А-55, В-12, В-22, І-11, І-15, І-23, І-31, К-05	19	А-55, В-12, В-22, Д-25, Д-32, Н-24, Н-31, Н-39, Н-51, М-34
3	А-21, А-43, А-55, В-12, В-22, К-07, К-14, К-19, Л-23, Л-29	20	А-55, В-12, В-22, Д-25, Д-32, М-45, М-47, М-50, А-21, А-43
4	А-21, А-43, А-55, В-12, В-22, Л-30, Л-41, Н-24, Н-31, Н-39	21	Д-37, Д-42, І-06, І-11, І-15, І-23, І-31, К-05, К-07, К-14
5	А-21, А-43, А-55, В-12, В-22, Н-51, М-34, М-45, М-47, М-50	22	Д-37, Д-42, І-06, І-11, І-15, К-19, Л-23, Л-29, Л-30, Л-41
6	Д-25, Д-32, Д-37, Д-42, І-06, І-11, І-15, І-23, І-31, К-05	23	Д-37, Д-42, І-06, І-11, І-15, Н-24, Н-31, Н-39, Н-51, М-34
7	Д-25, Д-32, Д-37, Д-42, І-06, К-07, К-14, К-19, Л-23, Л-29	24	Д-37, Д-42, І-06, І-11, І-15, М-45, М-47, М-50, А-21, А-43
8	Д-25, Д-32, Д-37, Д-42, І-06, Л-30, Л-41, Н-24, Н-31, Н-39	25	І-23, І-31, К-05, К-07, К-14, К-19, Л-23, Л-29, Л-30, Л-41
9	Д-25, Д-32, Д-37, Д-42, І-06, Н-51, М-34, М-45, М-47, М-50	26	І-23, І-31, К-05, К-07, К-14, Н-24, Н-31, Н-39, Н-51, М-34
10	І-11, І-15, І-23, І-31, К-05, К-07, К-14, К-19, Л-23, Л-29	27	І-23, І-31, К-05, К-07, К-14, М-45, М-47, М-50, А-21, А-43
11	І-11, І-15, І-23, І-31, К-05, Л-30, Л-41, Н-24, Н-31, Н-39	28	К-19, Л-23, Л-29, Л-30, Л-41, Н-24, Н-31, Н-39, Н-51, М-34
12	І-11, І-15, І-23, І-31, К-05, Н-51, М-34, М-45, М-47, М-50	29	К-19, Л-23, Л-29, Л-30, Л-41, М-45, М-47, М-50, А-21, А-43
13	К-07, К-14, К-19, Л-23, Л-29, Л-30, Л-41, Н-24, Н-31, Н-39	30	Н-24, Н-31, Н-39, Н-51, М-34, М-45, М-47, М-50, А-21, А-43
14	К-07, К-14, К-19, Л-23, Л-29, Н-51, М-34, М-45, М-47, М-50	31	В-22, Д-25, Д-32, Д-37, Д-42, І-06, І-11, І-15, І-23, М-47
15	Л-30, Л-41, Н-24, Н-31, Н-39, Н-51, М-34, М-45, М-47, М-50	32	А-55, В-12, К-05, К-07, К-14, Н-24, Н-31, М-34, М-45, М-47
16	А-55, В-12, В-22, Д-25, Д-32, Д-37, Д-42, І-06, І-11, І-15	33	І-11, І-15, І-23, І-31, К-19, Л-23, Л-41, Н-24, Н-31, М-50, А-21
17	А-55, В-12, В-22, Д-25, Д-32, І-23, І-31, К-05, К-07, К-14	34	А-43, В-22, Д-32, І-11, К-14, Л-30, Н-31, М-34, М-45

1. 
   визначити рівняння регресії залежності обсягу збуту від ціни для кожної моделі одягу;
   
2. 
   побудувати модель задачі нелінійного програмування з метою максимізації прибутку та визначити оптимальні ціни для кожної моделі одягу.
   
3. 
   визначити оптимальні обсяги збуту та собівартість для кожної моделі одягу.
   

ЛАБОРАТОРНА РОБОТА №12

ФОРМУВАННЯ ОПТИМАЛЬНОЇ ІНВЕСТИЦІЙНОЇ ПРОГРАМИ З МЕТОЮ ЗМЕНШЕННЯ РИЗИКУ ТА ЗРОСТАННЯ ПРИБУТКІВ ПІДПРИЄМСТВА
I. Загальні положення

В умовах загострення конкуренції на сучасному ринку постає задача про доцільність узгодження асортименту продукції підприємства з метою забезпечення зростання прибутків та зменшення ризику на основі застосування методів оптимізації. В таких випадках доцільно застосовувати багатокритеріальну оптимізацію. Пошук найкращих рішень за декількома критеріями називають багатокритеріальною чи векторною оптимізацією.
II. Теоретичні відомості

Функціонування економічної системи оцінюється певними критеріями, які можна записати у вигляді локальних критеріїв . Множину критеріїв можна представити у вигляді векторної функції мети (глобального критерію)



; (12.1)

.

де - вектор змінних величин.

Вирішенням такої задачі може бути тільки компромісне рішення.

Для вирішення задач векторної оптимізації використовуються такі методи:

• 
  методи, що ґрунтуються на згортанні критеріїв в один;
  
• 
  методи, що використовують обмеження на критерії тощо.
  

У методах, що ґрунтуються на згортанні критеріїв, із локальних критеріїв формується один. Найбільш розповсюдженим із них є метод лінійної комбінації часткових критеріїв. Припустимо, що заданий вектор вагових коефіцієнтів критеріїв , які характеризують важливість відповідного критерію, причому

У такому випадку задача математичного програмування стає однокритеріальною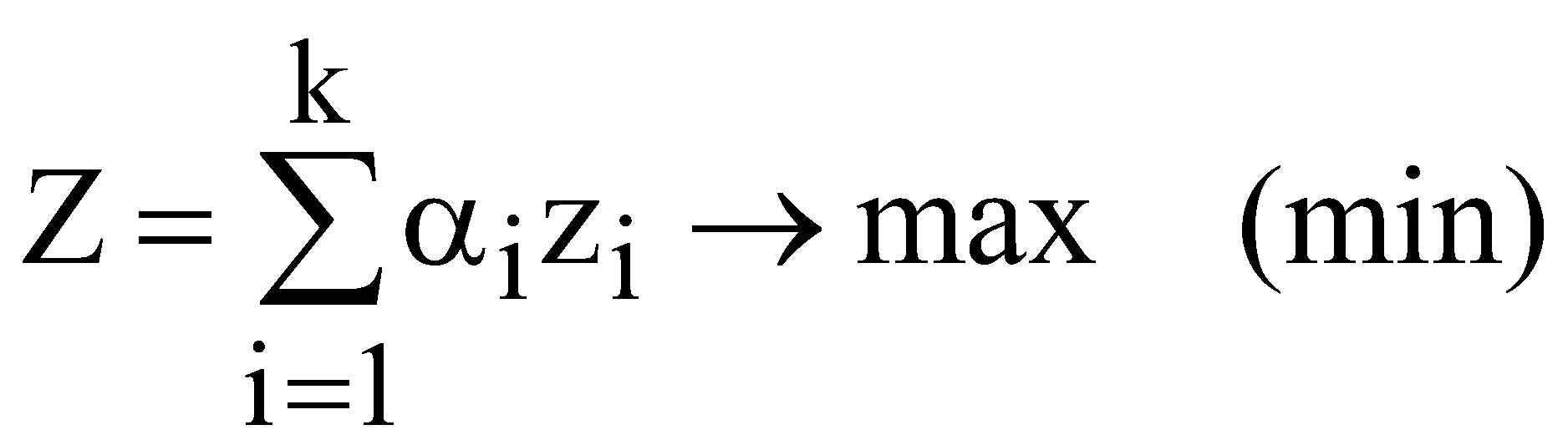



, (12.2)

.

В цьому випадку важливим є те, щоб локальні критерії були однонаправлені. Тому, щоб мінімізувати локальний критерій , достатньо максимізувати критерій (- ).

Для постановки задачі формування оптимальної інвестиційної програми введемо наступні позначення.

Позначимо – частки фінансових ресурсів від заданого бюджету, скерованих (інвестованих) у розвиток і-го виду діяльності підприємства.

Для моделі формування оптимальної інвестиційної програми можна застосувати дві цільові функції, перша з яких пов’язана з максимізацією очікуваних прибутків, а друга – з мінімізацією ризиків, викликаних взаємовпливами різних видів діяльності підприємства.

Модель матиме вигляд:

• 
  цільова функція – максимізація прибутку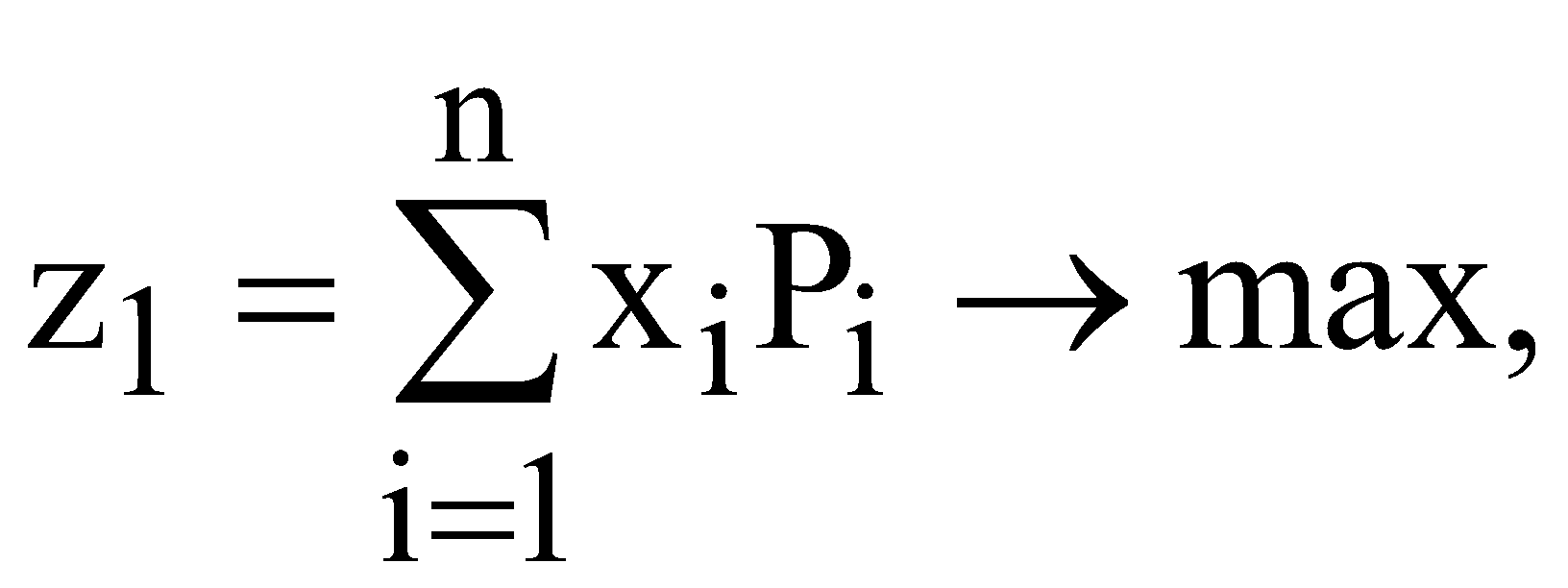
  

(12.3)

де - величина очікуваного прибутку підприємства за видами діяльності за рік;

• 
  цільова функція – мінімізація ризику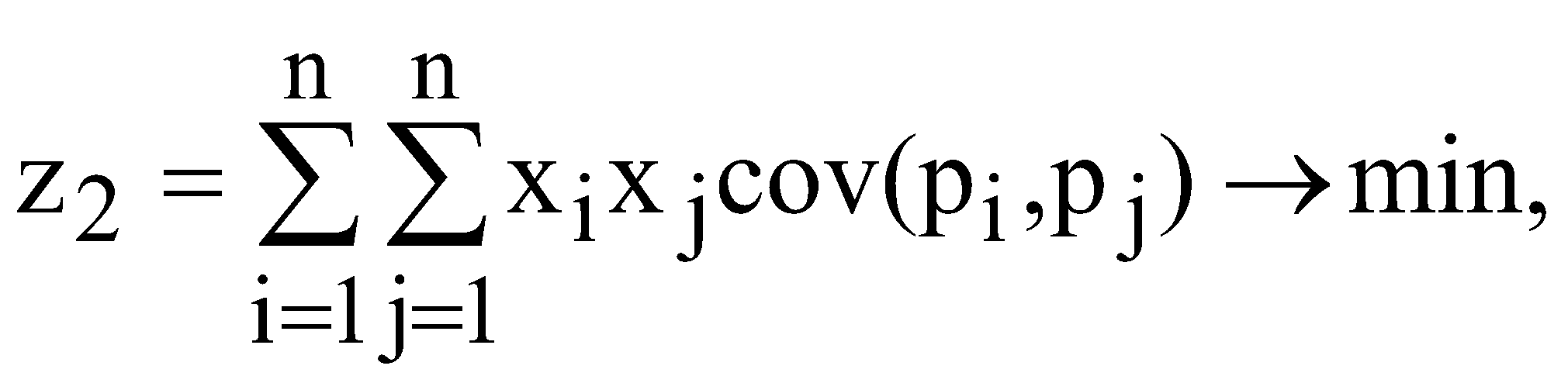
  

(12.4)

де - коваріація між величинами прибутків i-го та j-го виду діяльності підприємства.

Для аналізу прибутковості діяльності підприємства будується коваріаційна матриця, на головній діагоналі якої розташовані вибіркові дисперсії ознак, а інші елементи – вибіркові парні коефіцієнти коваріації (змішані дисперсії). Коваріаційна матриця є симетричною відносно головної діагоналі і кожен її елемент характеризує ступінь щільності ознак, тобто їх однорідність.

Модель формування оптимальної інвестиційної програми також містить систему обмежень:

1. Сума часток інвестицій у кожен з видів діяльності підприємства не може перевищувати 1. Тобто має виконуватись умова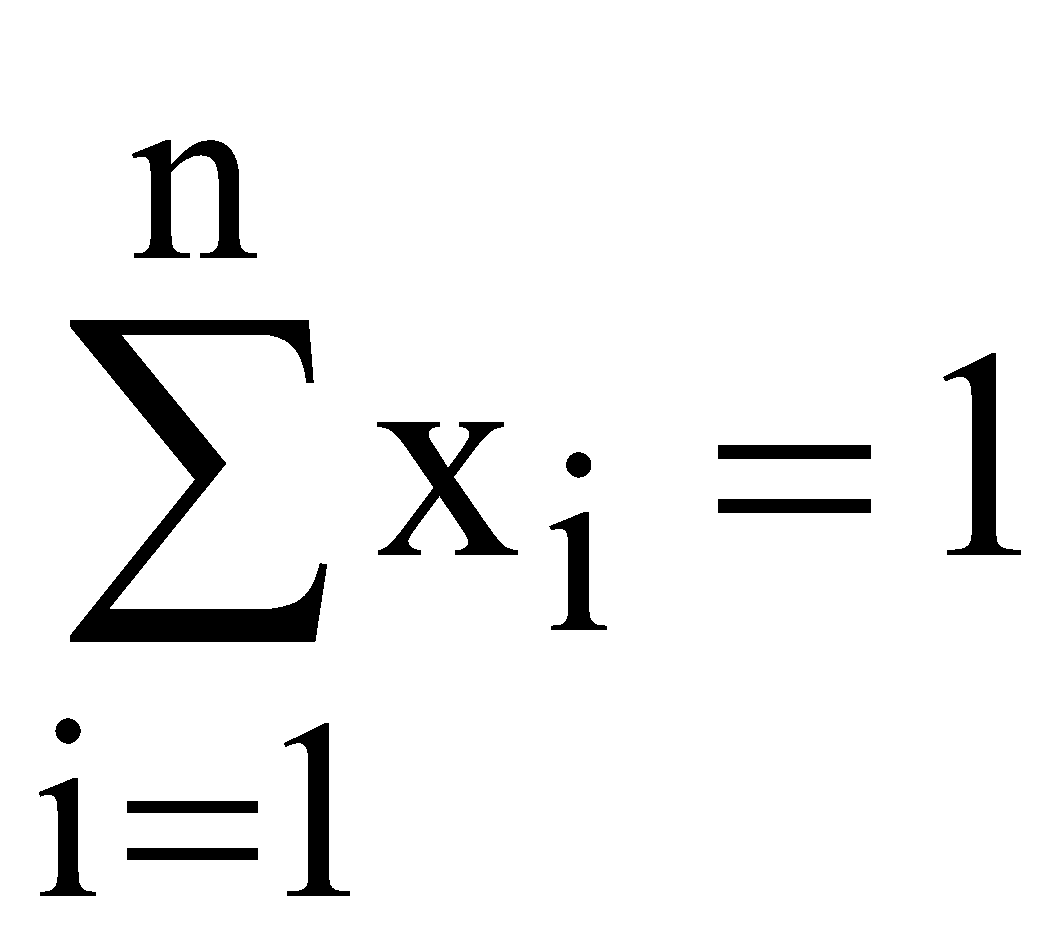

. (12.5)

2. Доцільно запровадити обмеження верхньої та нижньої межі інвестицій для кожного виду діяльності пропорційно до середньостатистичних даних минулих періодів

,

, (12.6)

…….

.

3. Доцільно ввести додаткові обмеження, пов’язані з взаємозалежністю різних видів діяльності, отримані з врахуванням оцінки чистих і змішаних дисперсій.