Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb. Скачать 3.77 Mb.
|
|
(5.9) де d – статистика може набувати будь-якого значення з інтервалу (0;4). При відсутності автокореляції d – статистика набуває значень близьких до 2. Для d – статистики визначені крайні межі (d1 – нижня, dn – верхня), які дозволяють із заданою надійністю дати відповідь, чи можна прийняти гіпотезу про відсутність автокореляції першого порядку чи ні. У залежності від значення d приймаємо, що: при при при при Якщо d – статистика набуває значення з п. 4, то для одержання відповіді про наявність автокореляції першого порядку необхідно збільшити кількість спостережень. Величина dn і dl для певних ймовірностей наводяться в статистичних таблицях. Якщо встановлено, що із заданою ймовірністю економетрична модель адекватна спостережувальним даним і соціально-економічні умови за період прогнозування змінюються за закономірностями, що мають місце і в базовому періоді, то точкова оцінка прогнозу знаходиться за формулою ІІІ. Завдання За певні періоди зібрані статистичні дані, які характеризують залежність між заощадженнями та доходом населення (табл. 5.1). Таблиця 5.1 Дані для визначення явищ гетероскедастичності та автокореляції
Для цих даних необхідно: перевірити наявність гетероскедастичності згідно з критерієм побудувати однофакторну модель; оцінити надійність моделі за допомогою критерію Фішера; перевірити наявність автокореляції за допомогою критерію Дарбіна-Уотсона; якщо модель адекватна згідно цих критеріїв, то визначити прогнозне значення заощаджень при величині доходів 28 млн. грн. ЛАБОРАТОРНА РОБОТА №6 МОДЕЛІ РОЗПОДІЛЕНОГО ЛАГУ. МЕТОД КОЙКА І. Загальні положення Для багатьох економічних процесів типовим є те, що ефект від впливу деякого фактора на показник, який характеризує процес, виявляється поступово, через деякий період. Причому вплив деяких факторів на показник може проявлятися не лише через певний період часу, а протягом певного часу. ІІ. Теоретичні відомості Економетрична модель розподіленого лагу має вигляд 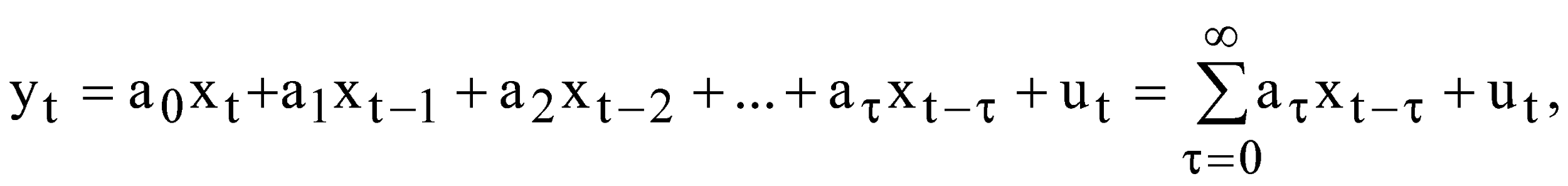 (6.1) (6.1)де Моделі розподілених лагів можуть задовільно описувати процеси лише в тому разі, коли забезпечена відносна стабільність умов, в яких ці процеси реалізуються. Така стабільність не завжди спостерігається для порівняно довгих проміжків часу, протягом яких формується сукупність спостережень. Це призводить до побудови узагальненої моделі розподіленого лагу 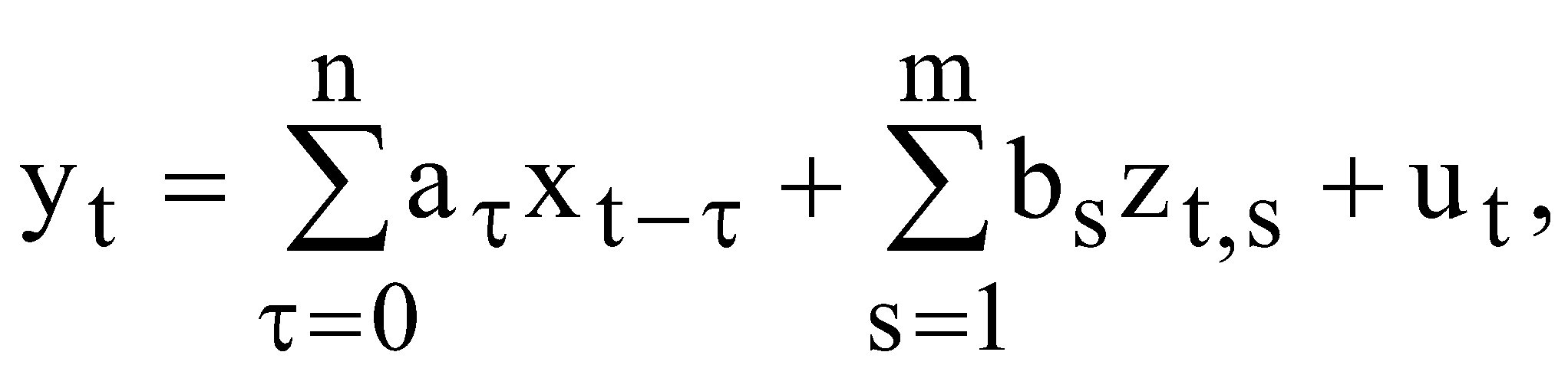 (6.2) (6.2)де Теоретично побудову моделі з розподіленими лагами можна узагальнити на будь-яку кількість незалежних змінних. Але практична реалізація такої моделі досить важка. Спостити розрахунки можна за допомогою методу Койка. Метод Койка використовується в тих випадках, коли з точки зору економіки факторна змінна має нескінченну лагову структуру і лагові параметри регресії володіють однаковим законом зміни. Запишемо регресію з лагами Припустимо, що 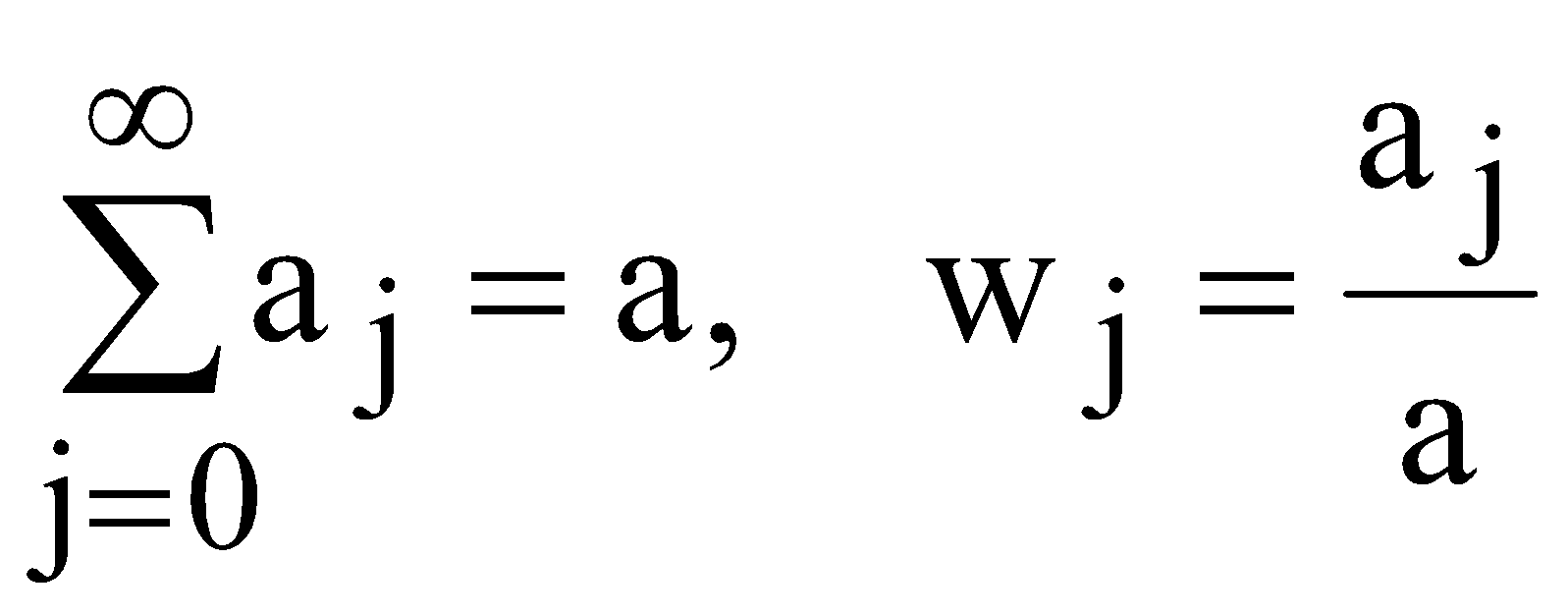 . (6.4) . (6.4)Тоді запишемо На всі ваги послідовність ваг утворюють геометричну прогресію. Оскільки послідовність ваг є геометричною прогресією, то Тоді запишемо Тепер можна записати регресію у вигляді Зробимо певні перетворення або Для оцінки значень Математично метод найменших квадратів подамо у вигляді 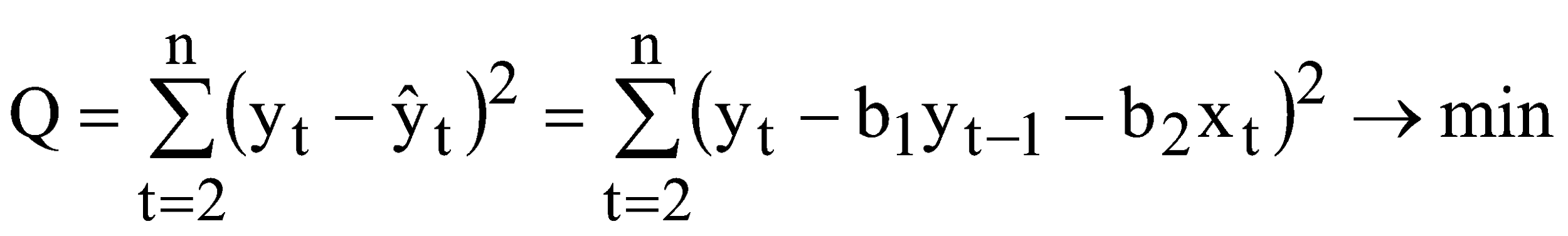 . (6.11) . (6.11)де Необхідною умовою існування мінімуму є рівність нулю часткових похідних по 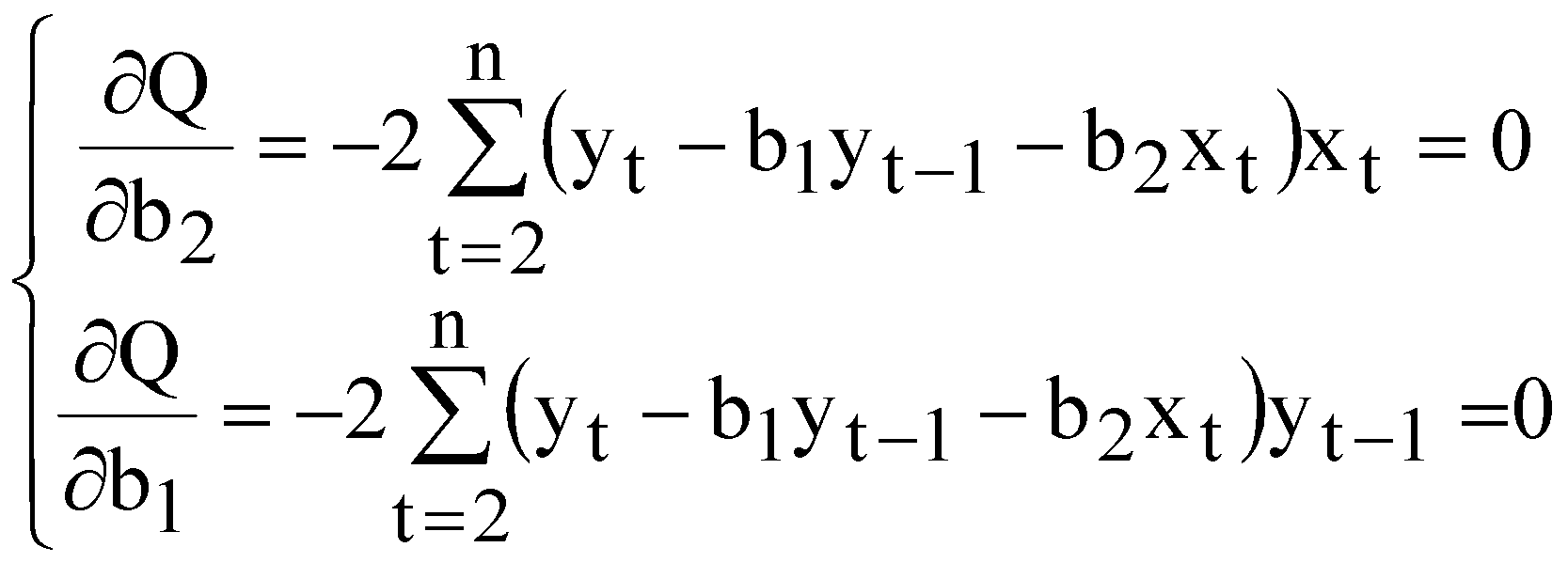 . (6.12) . (6.12)Розкриємо дужки і отримаємо систему нормальних рівнянь 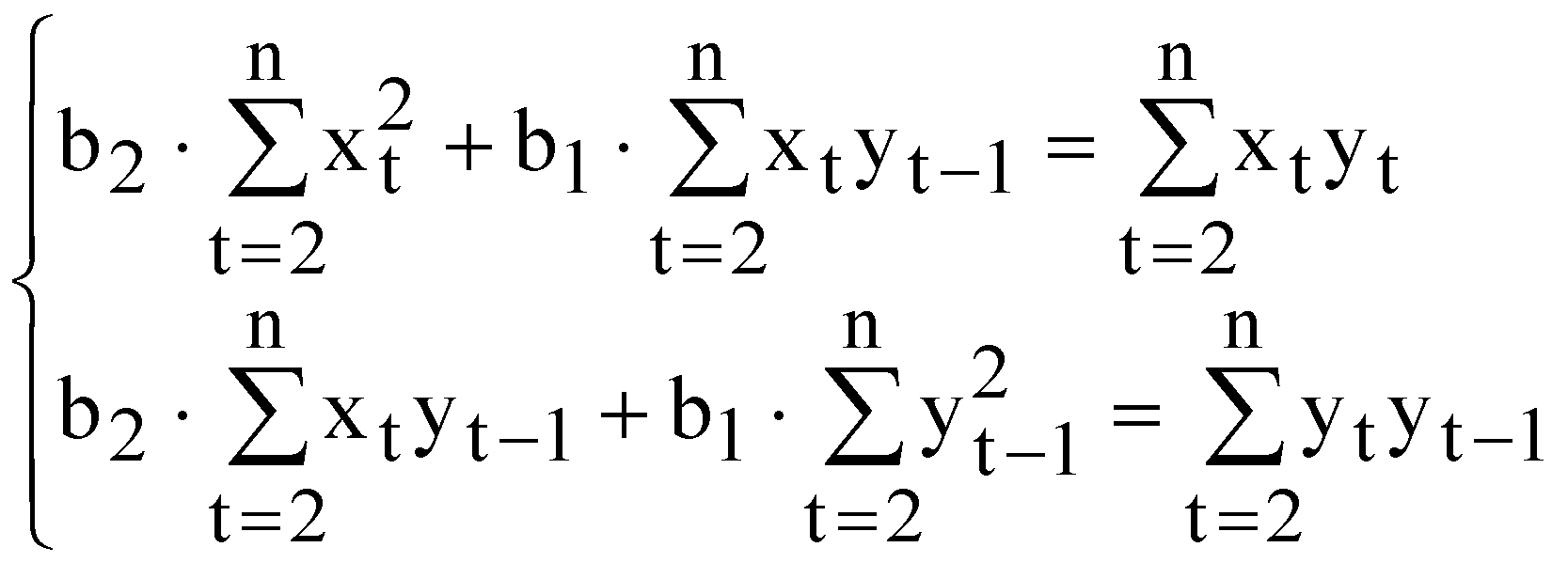 . (6.13) . (6.13)Невироджена система нормальних рівнянь має єдиний розв'язок. Щільність зв'язку між факторною і результативною ознаками можна знайти за допомогою коефіцієнта детермінації 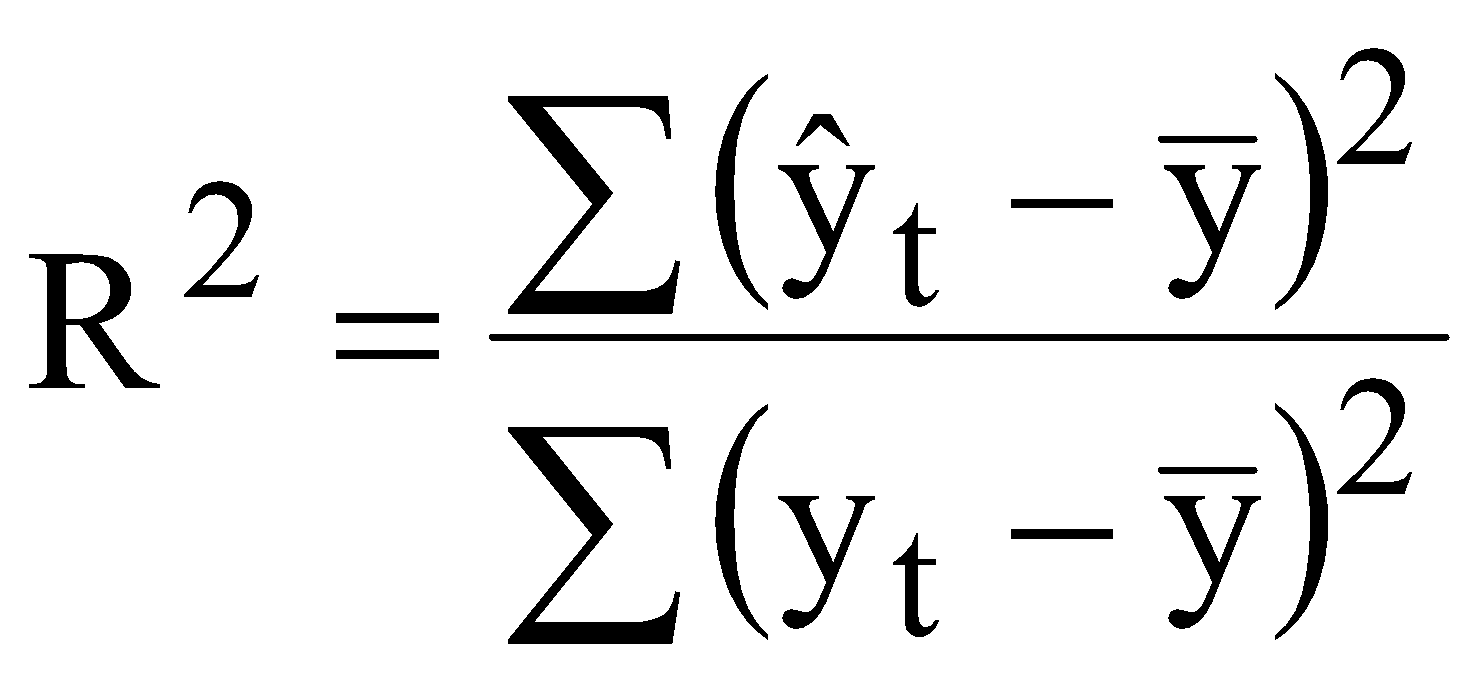 , (6.14) , (6.14)де Значення критерію Фішера і Дарбіна-Уотсона визначаються за формулами 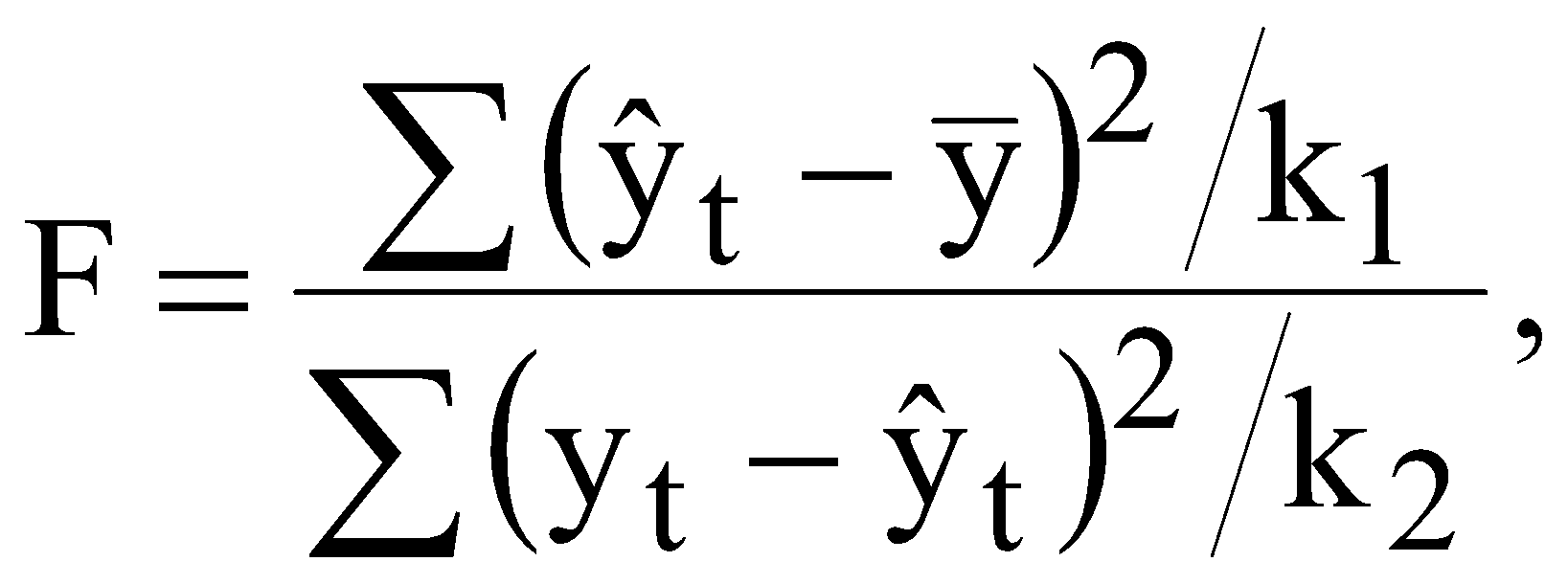 (6.15) (6.15)де 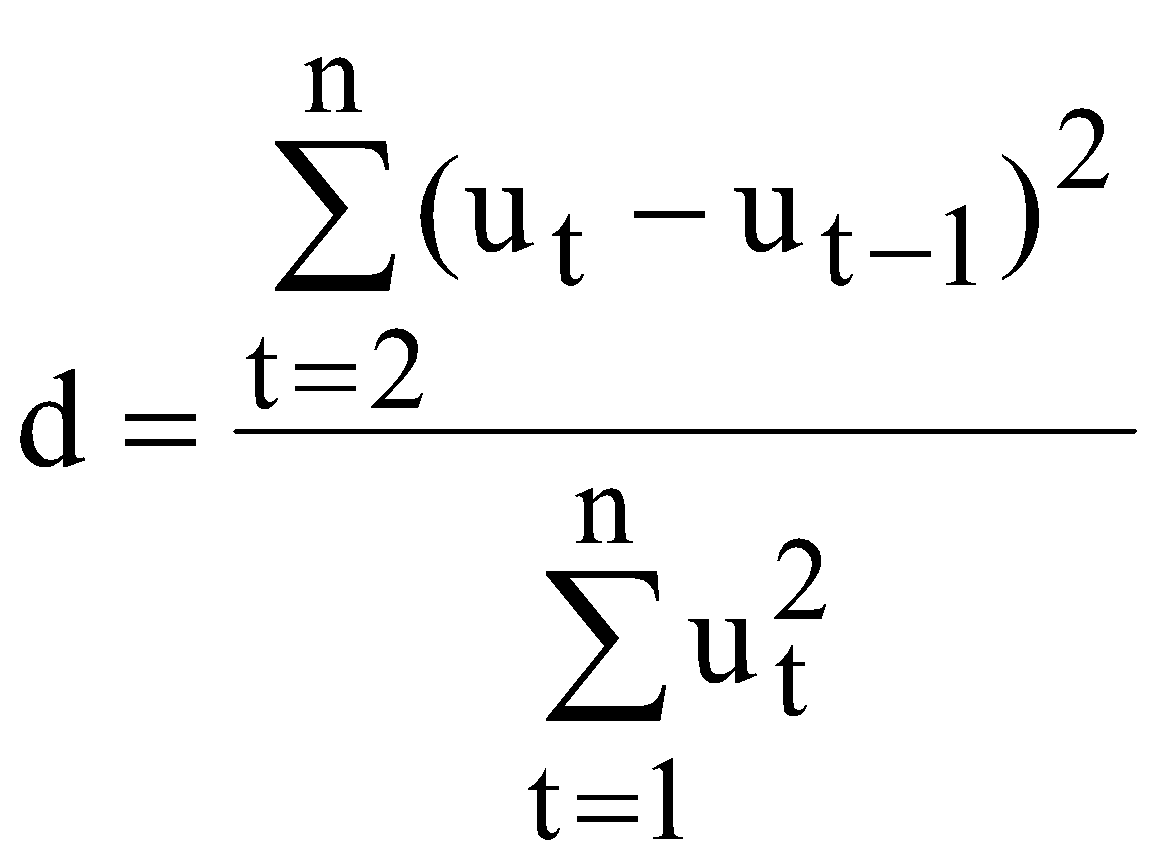 , , |
