Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb.
|
|
ЛАБОРАТОРНА РОБОТА №8 ВИЗНАЧЕННЯ ОПТИМАЛЬНОГО РІШЕННЯ ЗАДАЧІ ГРАФІЧНИМ МЕТОДОМ І. Загальні положення Для розв’язування двовимірних задач лінійного програмування, тобто задач із двома змінними, а також деяких тривимірних задач застосовують графічний метод, що ґрунтується на геометричній інтерпретації та аналітичних властивостях задач лінійного програмування. Обмежене використання графічного методу зумовлене складністю побудови багатогранника розв’язків у тривимірному просторі (для задач з трьома змінними), а графічне зображення задачі з кількістю змінних більше трьох взагалі неможливе. ІІ. Теоретичні відомості Розглянемо задачу. Визначити  (8.1)за ум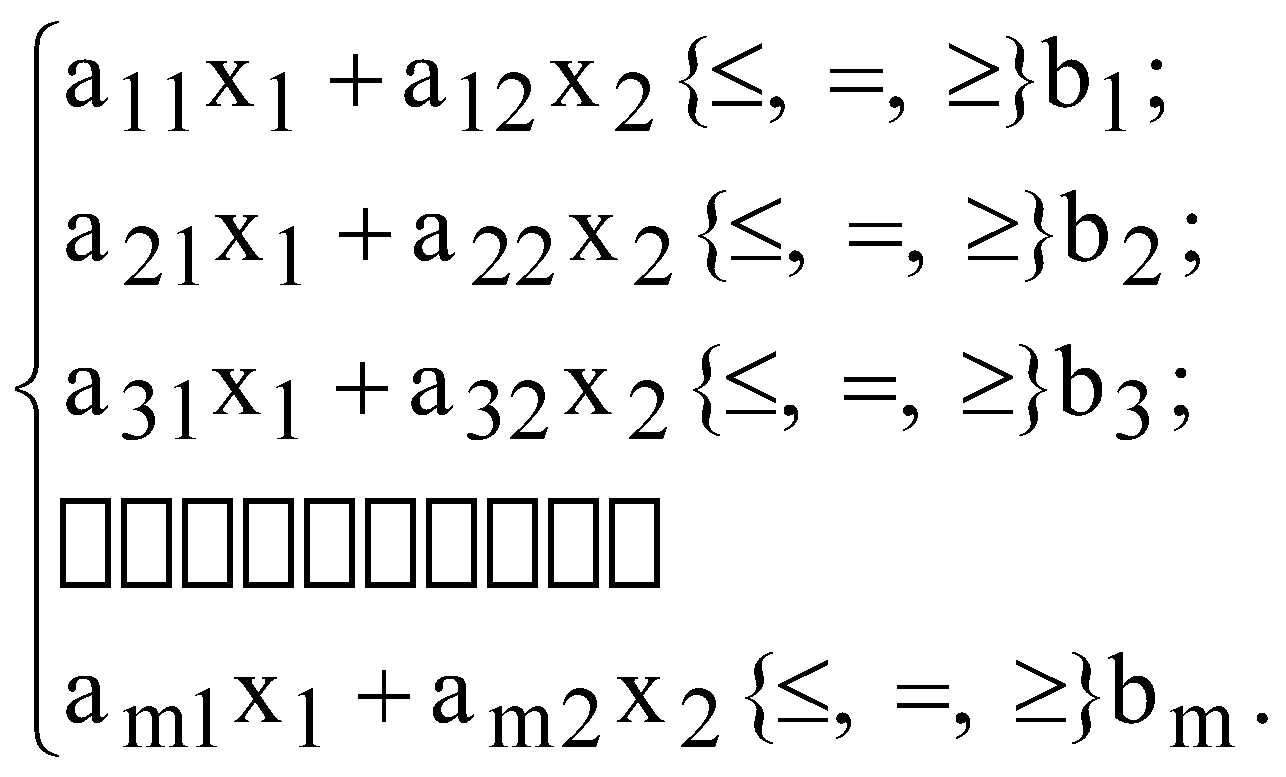ов  (8.2) . (8.3)Припустимо, що система (8.2) за умов (8.3) сумісна і багатокутник її розв’язків обмежений. Згідно з геометричною інтерпретацією задачі лінійного програмування кожне і-те обмеження-нерівність у (8.2) визначає півплощину з граничною прямою  (і = 1, 2, …, т). Системою обмежень (8.2) графічно можна зобразити спільну частину, або переріз усіх зазначених півплощин, тобто множину точок, координати яких задовольняють всі обмеження задачі — багатокутник розв’язків. Умова (8.3) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція задачі лінійного програмування геометрично інтерпретується як сукупність паралельних прямих с1х1 + с2х2 = const. Скористаємося для графічного розв’язання задачі лінійного програмування такими властивостями: якщо задача лінійного програмування має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатокутника розв’язків; якщо ж цільова функція досягає екстремального значення більш як в одній вершині багатокутника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією цих вершин. Отже, розв’язати задачу лінійного програмування графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (8.1) лінійна цільова функція набуває найбільшого (найменшого) значення. Алгоритм графічного методу розв’язування задачі лінійного програмування складається з таких кроків: 1. Будуємо прямі, рівняння яких отримуємо заміною в обмеженнях задачі (8.2) знаків нерівностей на знаки рівностей. 2. Визначаємо півплощини, що відповідають кожному обмеженню задачі. 3. Знаходимо багатокутник розв’язків задачі лінійного програмування. 4. Будуємо вектор  , що задає напрям зростання значення цільової функції задачі.5. Будуємо пряму с1х1 + с2х2 = 0, перпендикулярну до вектора  .6. Рухаючи пряму с1х1 + с2х2 = 0 в напрямку вектора  , знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального значення (перша вершина багатокутника – розв’язок задачі на мінімум, остання вершина - розв’язок задачі на максимум).7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці. ІІІ. Завдання Побудувати та розв’язати графічно задачу лінійного програмування згідно варіанту. Дати економічну інтерпретацію результатам розв’язку. Варіанти 1-5 На фермі кожна корова щоденно має отримувати не менше 9 частин зерна, не менше 8 частин сіна, не менше 12 частин висівок. Для годування тварин використовуються два види кормів. Кількість частин зерна, сіна та висівок у кожному виді кормів та вартість 1 кг кормів наведено у табл. 8.1. Складіть денний раціон необхідної поживності, мінімізуючи при цьому витрати на придбання кормів. Таблиця 8.1 Норми витрат ресурсів та вартість 1 кг кормів
Варіанти 6-10 Для виготовлення двох видів болтів А і Б завод використовує як сировину сталь і кольорові метали, запаси яких обмежені. На виготовлення вказаних двох виробів задіяні токарні і фрезерні верстати (табл. 8.2). Визначити план випуску продукції, при якому буде досягнутий максимальний прибуток. Таблиця 8.2 Норми витрат ресурсів та прибуток від реалізації готової продукції
Варіанти 11-15 У четвер їдальня готує два види страв – зрази та котлети. Для приготування використовується м’ясо, крупа, картопля. Норми витрат продуктів для приготування та прибуток від реалізації 100 г. страви наведено у табл. 8.3. Розрахувати максимальний прибуток їдальні у четвер. Таблиця 8.3 Норми витрат продуктів та прибуток від реалізації 100 г страви
Варіанти 16-20 Підприємство хімічної промисловості випускає сірчану і соляну кислоту. Випуск 1 т соляної кислоти приносить прибуток в розмірі 125 грн., а сірчаної – 235 грн. При виробництві 1 т сірчаної кислоти створюється 0,5+0,01·р т небезпечних відходів, а при виробництві 1 т соляної кислоти – 1,2 т. Держзамовлення на сірчану кислоту складає 100+р т, а на соляну – 200+р т. Сумарний обсяг небезпечних речовин не має перевищувати 600+р т, інакше на підприємство накладаються штрафні санкції. Скласти план виробництва кислот для отримання максимального прибутку. Ринкові дослідження показали, що попит кожен вид кислоти, сірчану та соляну, складав у попередньому періоді 400 т на рік. Варіанти 21-25 Підприємство виготовляє два види добрив "Флора" та "Паросток". Для виробництва добрив використовують азотну кислоту, аміак та калійну сіль. Норми витрат сировини, її запаси на підприємстві, а також прибуток від реалізації 100 кг добрива наведені в табл. 8.4. Визначити, скільки підприємство має виготовляти і реалізовувати добрив для отримання максимального прибутку. Таблиця 8.4 Норми витрат сировини і прибуток від реалізації 100 кг добрива
Варіанти 26-30 Для виготовлення двох видів пального П1 та П2 використовують три види сировини: бензин, керосин, дизельне пальне. Запаси ресурсів, норми витрат ресурсів, а також величина прибутку, що отримують від реалізації 1 кг пального наведено у табл. 8.5. Необхідно скласти план виробництва пального за умов реалізації якого підприємство отримує максимальний прибуток. Таблиця 8.5 Норми витрат ресурсів та величина прибутку від реалізації 1 кг пального
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||