Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb.
|
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ "ЛЬВІВСЬКА ПОЛІТЕХНІКА" ЕКОНОМІКО-МАТЕМАТИЧНІ МЕТОДИ І МОДЕЛІ МЕТОДИЧНІ ВКАЗІВКИ до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти галузі знань 07 "Управління та адміністрування" спеціальностей 056 "Міжнародні економічні відносини", 072 "Фінанси, банківська справа та страхування", 075 "Маркетинг" Затверджено на засіданні кафедри маркетингу і логістики Протокол № 7 від 15.01.2018 р. Львів – 2018 Економіко-математичні методи і моделі: Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти галузі знань 07 "Управління та адміністрування" спеціальностей 056 "Міжнародні економічні відносини", 072 "Фінанси, банківська справа та страхування", 075 "Маркетинг" / Укл.: О.Б. Мних, О.Б. Гірна, Н.Є. Кузьо, С.В. Леонова, І.С. Рикованова. – Львів: Видавництво Національного університету "Львівська політехніка", 2018. – 59 с. Укладачі: Мних О.Б., д-р екон. наук, проф., Гірна О.Б., канд. екон. наук, доц., Кузьо Н.Є., старший викладач, Леонова С.В., канд. екон. наук, старший викладач , Рикованова І.С., старший викладач Відповідальний за випуск: Костюк О.С., канд. екон. наук, доц. Рецензенти: Глинський Н.Ю., канд. екон. наук, доц., Косар Н.С., канд. екон. наук, доц. ЗМІСТ Вступ…………………………………………………………………………………4 Лабораторна робота №1. Побудова моделі міжгалузевого балансу…………..…5 Лабораторна робота №2. Побудова лінійної економетричної моделі та дослідження її адекватності…………………………………….…..9 Лабораторна робота №3. Виробнича регресія……………………………….…..13 Лабораторна робота №4. Побудова лінійної багатофакторної моделі та дослідження її адекватності…………………………………….....19 Лабораторна робота №5. Визначення гетероскедастичності та автокореляції залишків…………………………………………………………… 25 Лабораторна робота №6. Моделі розподіленого лагу. Метод Койка……….. 29 Лабораторна робота №7. Прийняття рішень в умовах повної невизначеності……………………………………………………. 33 Лабораторна робота №8. Визначення оптимального рішення задачі графічним методом…………………………………………………………….38 Лабораторна робота №9. Побудова лінійної моделі оптимізаційної задачі та її аналіз………………………………………………………………..42 Лабораторна робота №10. Побудова моделі транспортної задачі та її аналіз………………………………………………………………..47 Лабораторна робота №11. Визначення оптимальних цін для отримання максимального прибутку………………………………………….51 Лабораторна робота №12. Формування оптимальної інвестиційної програми з метою зменшення ризику та зростання прибутків підприємства………………………………………………….……55 Рекомендована література………………………………………………………..58 ВСТУП Економіка як наука про об’єктивні причини розвитку суспільства ще з ранніх часів у своїх діяльності користується різноманітними кількісними характеристиками, і тому вона акумулювала в собі велику кількість математичних методів. Сьогодні в економічній науці на перший план ставиться математична модель як дієвий інструмент дослідження та прогнозування розвитку економічних процесів і явищ. Математичну модель можна представити як систему математичних співвідношень без протиріч, яка служить дієвим інструментом відтворення певного класу якісних або кількісних функціональних характеристик, властивих економічному процесу чи явищу, що вивчається. Вона розвиває уявлення про закономірності та взаємозв’язки економічних процесів і допомагає формуванню наукового мислення та навичок порівняльного аналізу на новому, більш високому рівні. Тому для визначення характерних особливостей класу математичних моделей, які застосовуються в економіці, використовується термін "економіко-математичне моделювання". Економіко-математичне моделювання як навчальна дисципліна поєднує теорію трьох дисциплін – економіки, математики та інформатики. Дисципліна показує, як застосовувати набуті знання до вирішення конкретних виробничих або інших ситуацій, головною метою яких є безкризове, стабільне функціонування відповідних інституцій при будь-яких змінах навколишнього ринкового середовища. В іноземних журналах і монографіях оперування математичним апаратом стала необхідною умовою для вирішення завдань соціально-економічного розвитку. Міжнародна практика переконує у високій ефективності застосування математичних методів при розв’язанні задач різних рівнів і напрямків економічного розвитку, в тому числі при дослідженні механізмів функціонування економічних систем. Разом із тим інструментарій математичного моделювання не дає однозначних відповідей чи рекомендацій, проте сприяє проведенню імітаційних розрахунків із використанням моделей при виборі різноманітних співвідношень параметрів або сценаріїв дій. ЛАБОРАТОРНА РОБОТА №1 ПОБУДОВА МОДЕЛІ МІЖГАЛУЗЕВОГО БАЛАНСУ І. Загальні положення Кожна економіка розвивається в складній мережі міжгалузевих взаємозв’язків. Зрозуміти вплив однієї галузі на іншу шляхом простого сумування неможливо. Наприклад, попит на автомобілі впливає не тільки на автомобільну промисловість, але й здійснює непрямий вплив і на металургію - виробника сировини для виготовлення автомобілів, і на галузі, які пов’язані з виробництвом шин і інших комплектуючих, а також і на галузі, які виробляють радіоприймачі, кондиціонери тощо. Способи аналізу, які розроблені для вирішення проблем взаємних зв’язків, необхідні для формування економічних планів, які послідовно пов’язували б змінні макрорівня з змінними мікрорівня. Метод міжгалузевого аналізу, який ще називають аналізом витрати-випуск, що розробив економіст В.В. Леонтьєв, дозволяє дати послідовні і чисельно визначені відповіді на питання, пов’язані з міжгалузевими взаємодіями і їх впливом на основні макроекономічні показники. IІ. Теоретичні відомості В економіці зв’язок між цілями і засобами встановлено таким чином  ,де засіб (ціль нижчого рівня) є незалежною змінною, мета (ціль вищого рівня) - залежною. В міжгалузевому аналізі прийнято обернене відношення:  .З точки зору математики міжгалузевий аналіз базується на використанні статистичних таблиць, які називаються "міжгалузевими", що відтворюють динаміку економіки протягом року і свідчать про зв’язок між галузями. Припустимо, що весь суспільний продукт в певний період часу виробляється n галузями. Позначимо  - обсяг випуску продукції і-ої галузі;  - обсяг продукції і-ої галузі, що використовується в j-ій (міжгалузеві поставки);  - обсяг продукції і-тої галузі, що не йде у виробництво, а йде на споживання. Ця величина складає кінцевий продукт і-ої галузі. Таблиця міжгалузевого балансу матиме вигляд табл. 1.1.В табл. 1.1 в кожному рядку подано розподіл кожного виду продукції. Кожен рядок характеризується балансом виду Випуск даного виду продукції = Проміжний попит + Кінцевий попит Таблиця 1.1 Таблиця міжгалузевого балансу
Математично 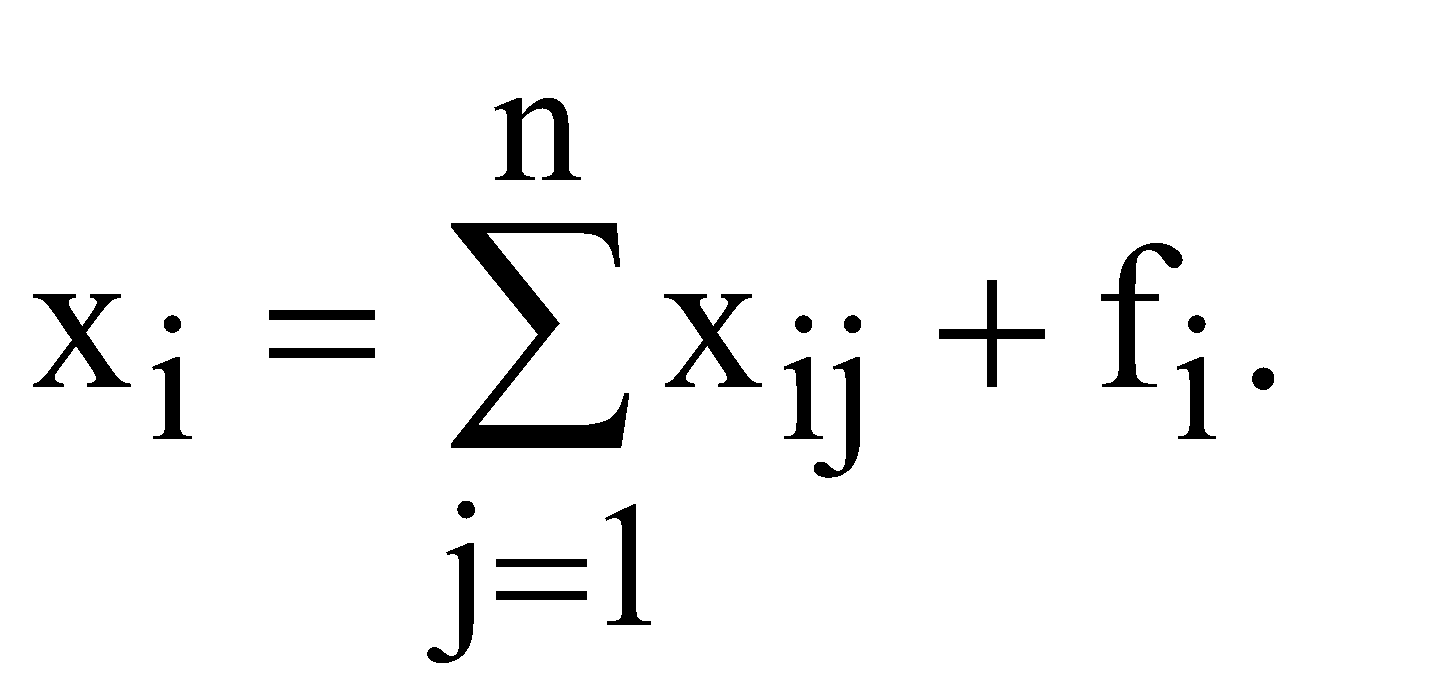  (1.1)Проміжний попит - це частина загального попиту, що використовується іншими галузями для своїх потреб. Кінцевий попит - частина попиту, який представляє собою закупки кінцевих продуктів - споживчих чи інвестиційних. Стовпці таблиці показують структуру витрат або структуру використовуваних ресурсів, які необхідні для кожної галузі. Для стовпців теж встановлюється баланс Випуск даного виду продукції = Проміжні витрати + Додана вартість Математично: 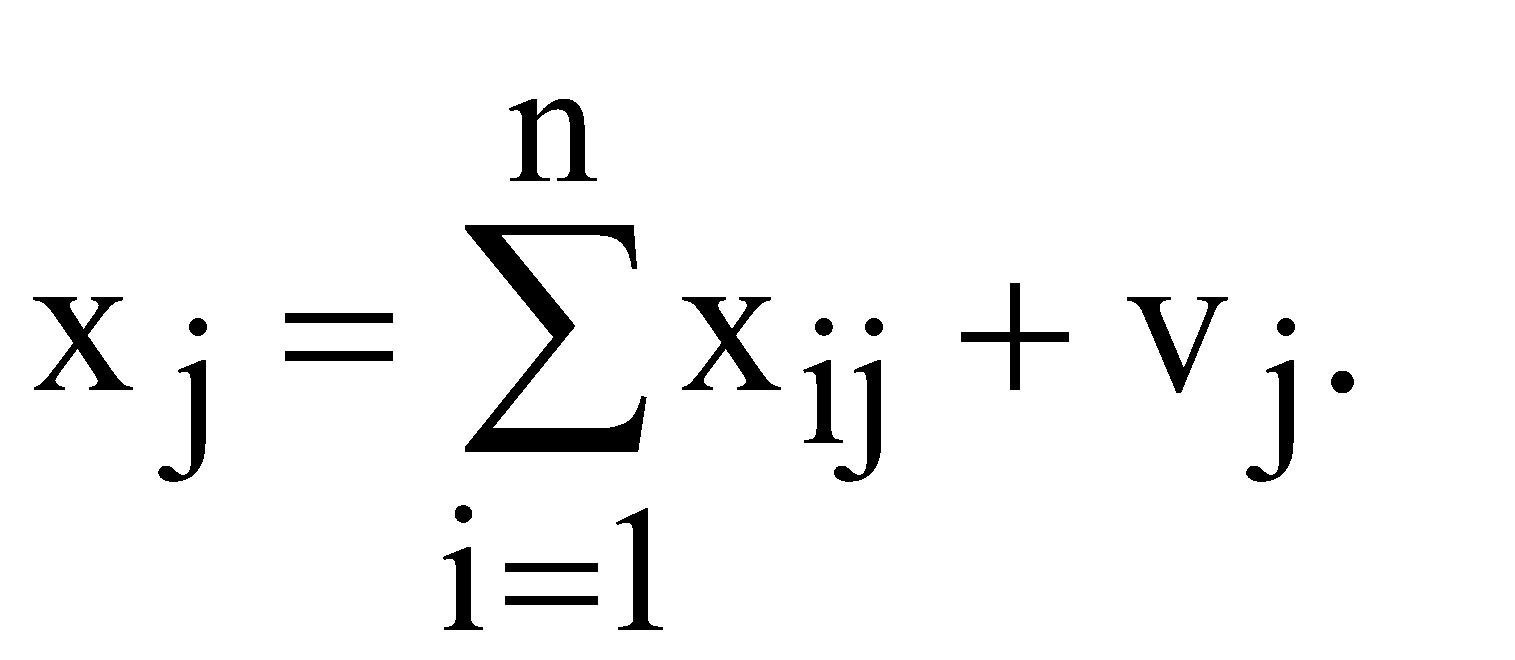  (1.2)Проміжні витрати представляють собою сировину, матеріали тощо, які закупила галузь j у інших галузей. Додана вартість - це новостворена вартість, яка поділяється на дохід тих, хто працює по найму (заробітну плату), амортизаційні відрахування, підприємницький дохід (прибуток) тощо. Для рядків і стовпців таблиці міжгалузевого балансу мають місце тотожності 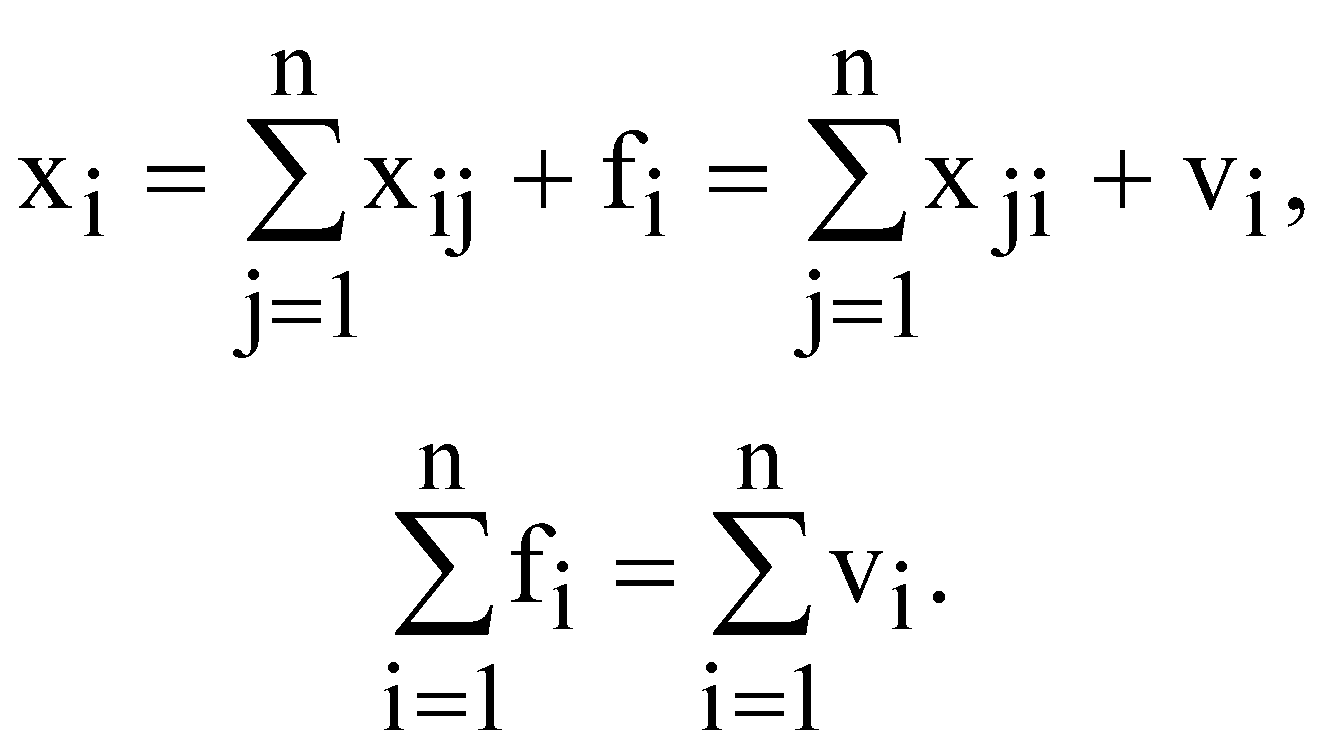 (1.3)Таблиця міжгалузевого балансу дозволяє вивчати структуру потоків ресурсів, однак для розуміння функціонування економіки необхідно побудувати матриці коефіцієнтів прямих витрат і коефіцієнтів повних витрат. Коефіцієнти прямих витрат (  ) - це кількість продукції і-ої галузі, яка необхідна для виготовлення одиниці продукції j-тої галузі. Очевидно, що  (1.4)Підставивши формулу (1.4) в (1.1) , отримаємо 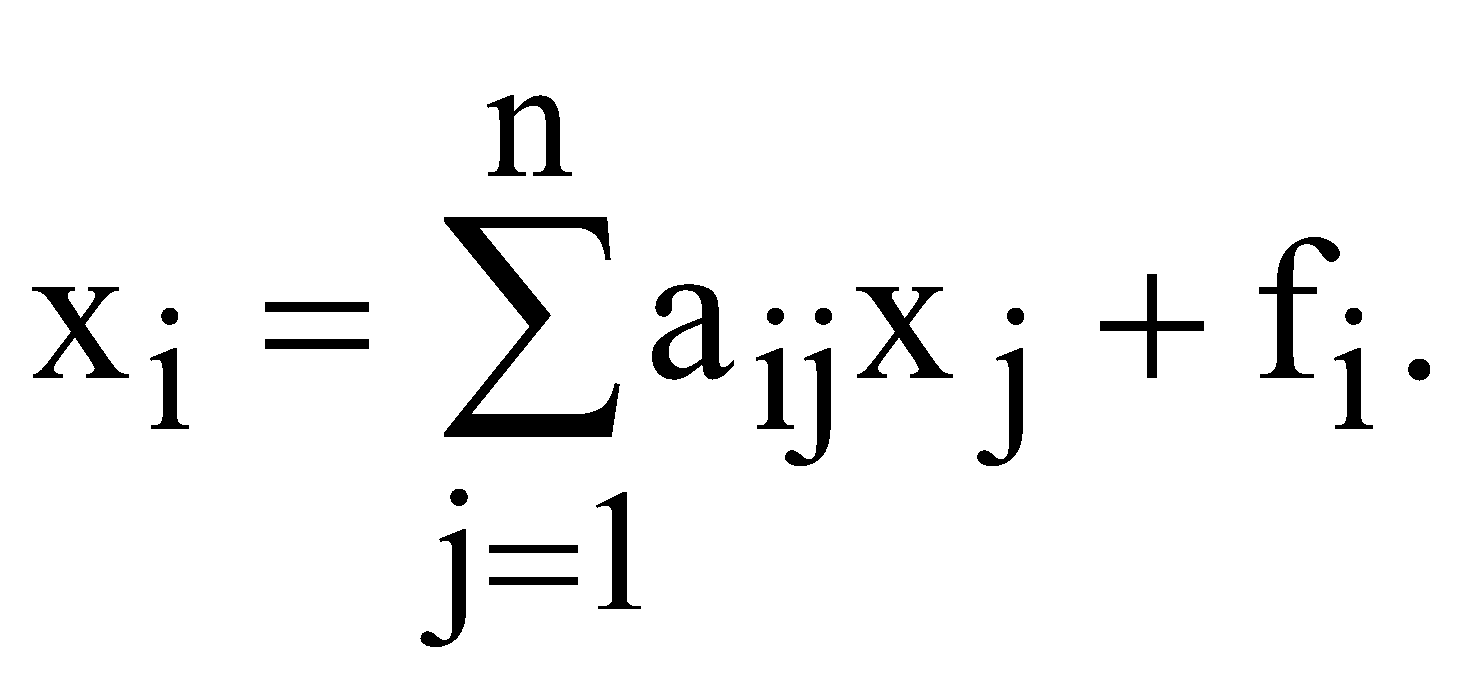 (1.5)Відношення (1.5) можна записати у вигляді системи рівнянь 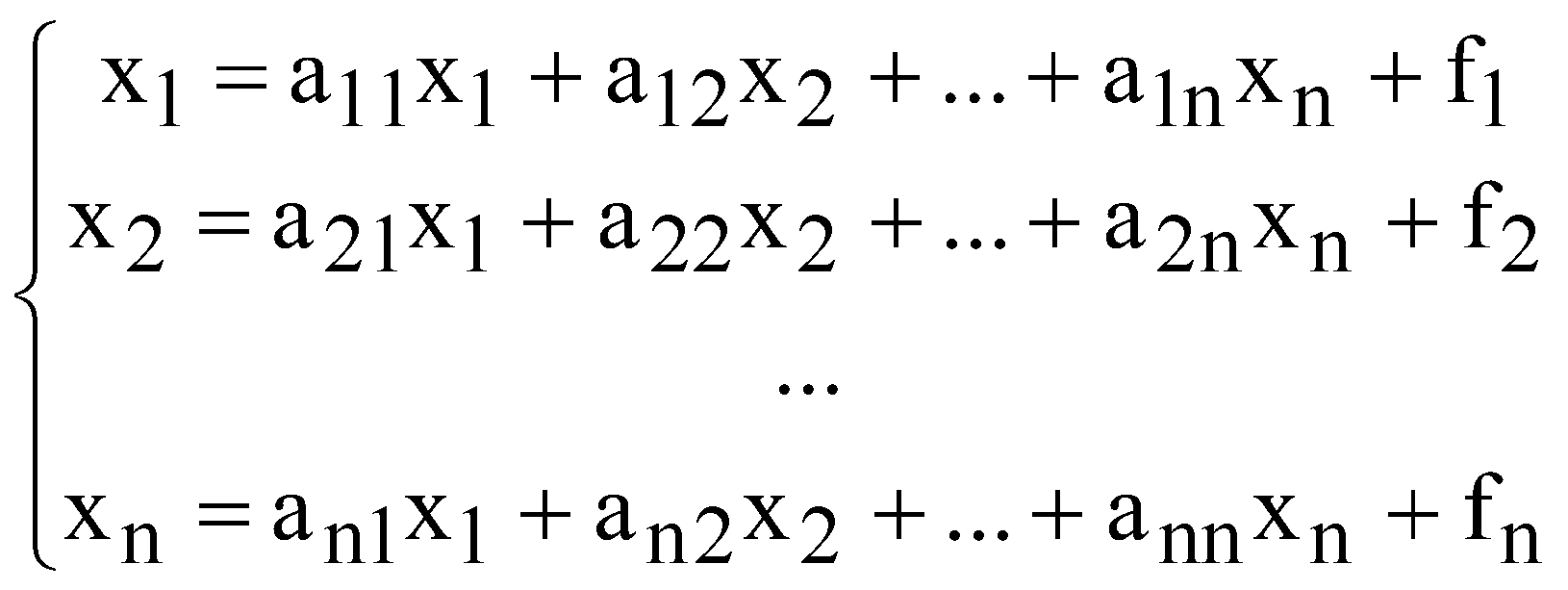 . (1.6)В векторному виді ця система набуде такого вигляду  . (1.7)Таким чином отримали модель міжгалузевого балансу Леонтьєва. Отже, можна поставити центральне питання міжгалузевого балансу - як зміниться обсяг випуску галузі 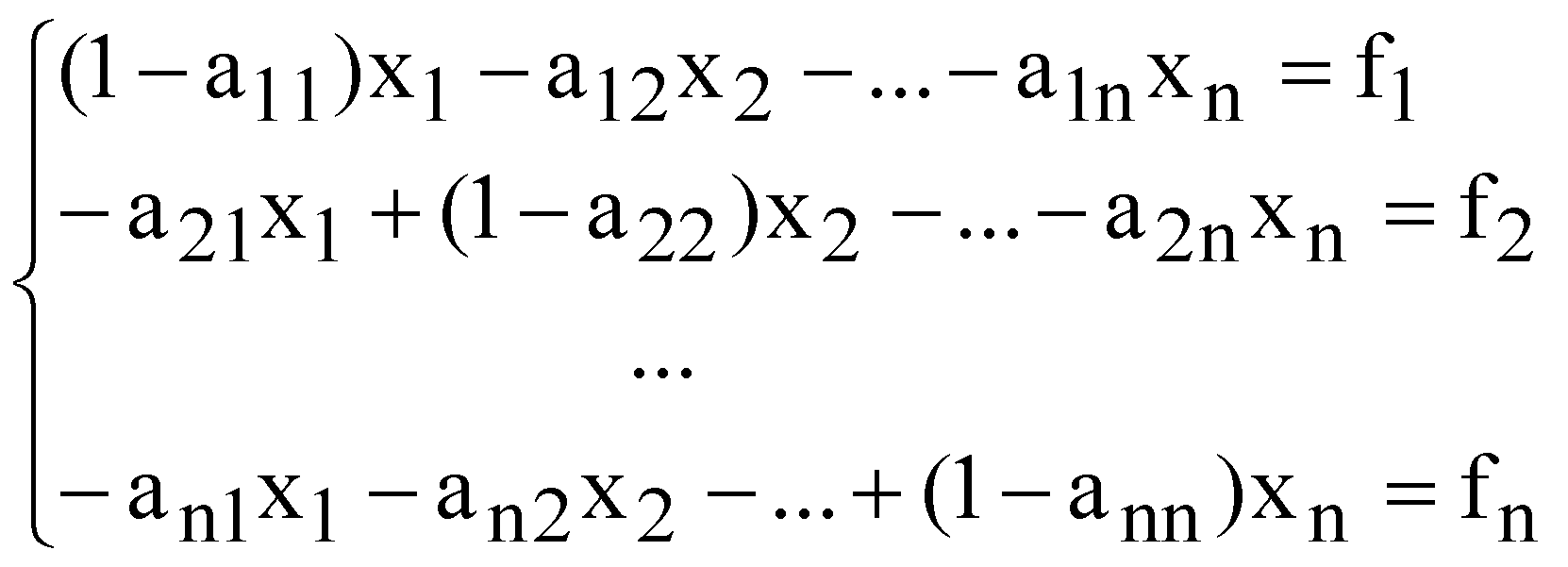, якщо при фіксованому значенні коефіцієнта прямих витрат аij значення зміниться на  , тобто для кожної галузі допускається існування виробничої функції з незмінним ефектом масштабу (витрати прямо пропорційні випуску) і з відсутністю взаємозаміни ресурсів (співвідношення затрат ресурсів фіксоване і не залежить від рівня випуску). Щоб відповісти на поставлене питання, необхідно знайти значення х1, х2, …….хn із системи лінійних рівнянь . (1.8)В векторному виді ця система набуде такого вигляду  . (1.9)Матриця коефіцієнтів прямих витрат А - невід’ємна квадратична матриця. Можна стверджувати, що для довільного додатного вектора кінцевого попиту F дане векторне рівняння має додатній розв’язок, який визначається так  , (1.10)де Е - одинична матриця розмірності n. Матриця В = (Е - А)-1 називається оберненою матрицею Леонтьєва або мультиплікатором Леонтьєва. Обернена матриця Леонтьєва В - це матриця коефіцієнтів повних витрат. Економічний зміст коефіцієнтів повних витрат полягає в наступному - елементи матриці В bij показують потребу в валовому випуску продукції галузі і для виробництва одиниці кінцевої продукції галузі j. Значення bij складаються із коефіцієнтів прямих і непрямих витрат та їх можна визначити за формулою  . (1.11)Непрямі витрати – це витрати продукції і-ої галузі в усіх галузях, що поставляють свою продукцію в j-ту галузь. Таким чином, В - це мультиплікатор, який показує ефект розповсюдження попиту, початковим джерелом якого є попит на кінцеву продукцію. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
