Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb. Скачать 3.77 Mb.
|
|
ІІІ. Завдання За даними табл. 1.2 необхідно визначити: Таблиця 1.2 Дані для побудови моделі міжгалузевого балансу
р – номер варіанту, який відповідає порядковому номеру в академічній групі. валовий обсяг випуску кожної галузі; міжгалузеві поставки; обсяг чистого продукту кожної галузі; коефіцієнти повних витрат. Як зміниться обсяг випуску продукції галузей ЛАБОРАТОРНА РОБОТА №2 ПОБУДОВА ЛІНІЙНОЇ ЕКОНОМЕТРИЧНОЇ МОДЕЛІ ТА ДОСЛІДЖЕННЯ ЇЇ АДЕКВАТНОСТІ І. Загальні положення Розвиток та широке застосування обчислювальної техніки сприяє виявленню закономірностей, зв'язку та динаміки реальних соціально-економічних явищ в економічному просторі. Економіко-математичні моделі, побудовані на основі статистичних рядів, мають не тільки пізнавальну, а й практичну цінність у прогнозуванні, плануванні, управлінні тощо. ІІ. Теоретичні відомості Зв'язок між різними явищами в економіці складний і різноманітний. На показник можуть впливати багато факторів, рівень впливу яких різний. Ці закономірності необхідно враховувати під час планування, прогнозування і проведення економічного аналізу. Серед парних регресій найбільш поширеною і простою в практиці моделювання є парна лінійна регресія. Парні лінійні регресійні моделі встановлюють лінійну залежність між двома змінними. При цьому одна із змінних вважається залежною змінною (у) та розглядається як функція від незалежної змінної (х). У загальному вигляді проста лінійна регресійна модель записується наступним чином де u – випадкові відхилення (залишки). Для того, щоб мати явний вигляд залежності (2.1), необхідно знайти (оцінити) невідомі параметри Для побудови економетричної моделі використаємо метод найменших квадратів (МНК). МНК полягає у наступному: теоретична лінія повинна перебувати на оптимальній віддалі від фактичних значень. Математично 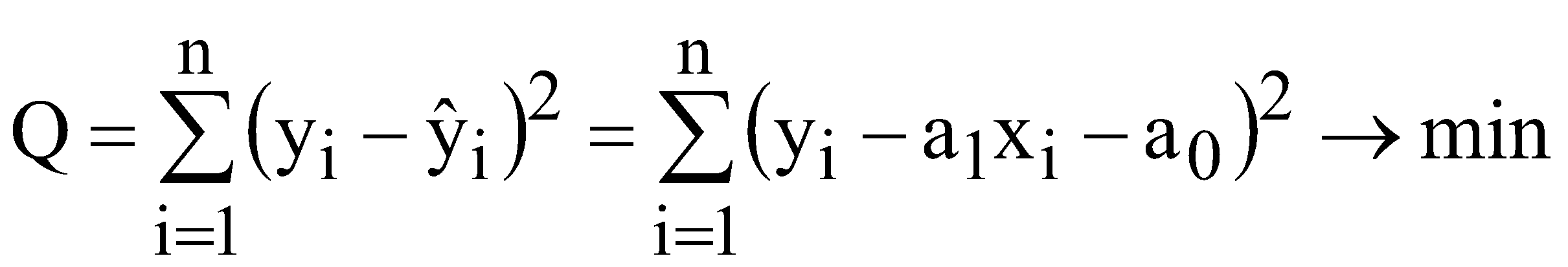 . (2.3) . (2.3)де Необхідною умовою існування мінімуму є рівність нулю часткових похідних функціоналу Q по 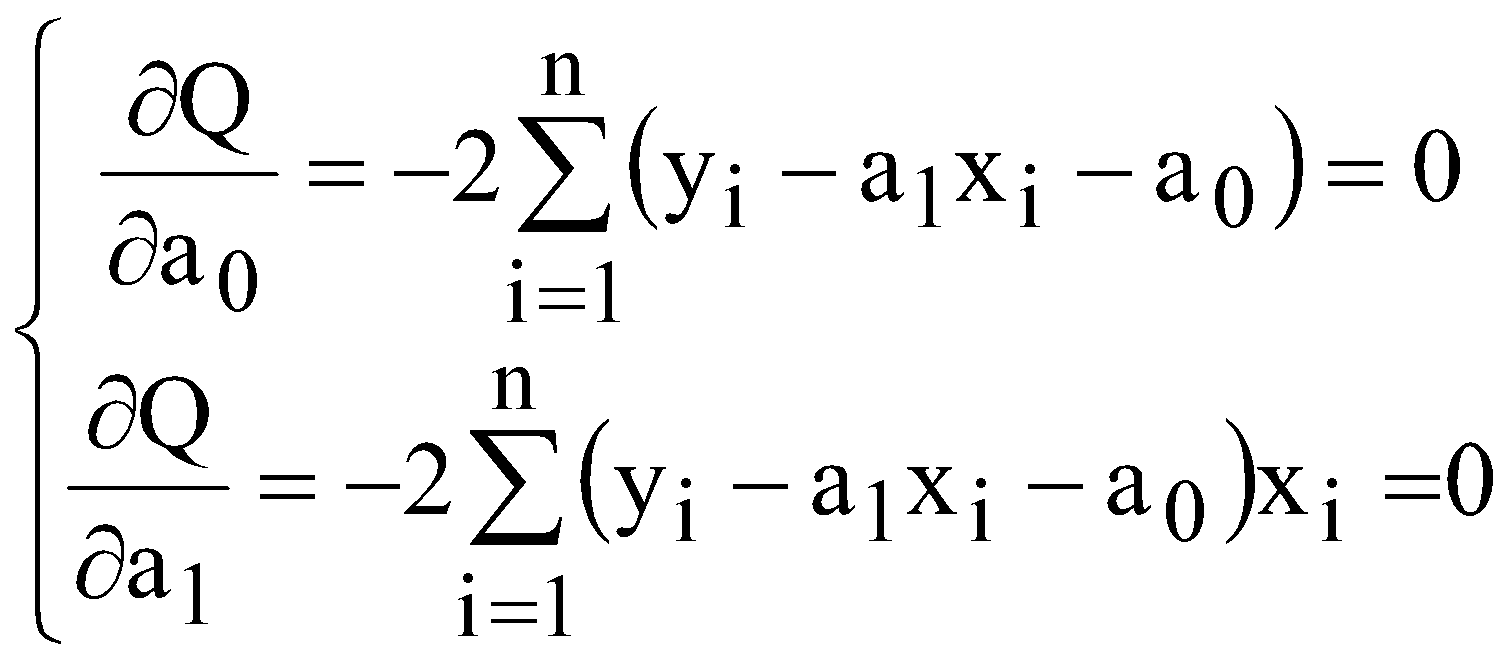 . (2.4) . (2.4)Розкриємо дужки і отримаємо систему нормальних рівнянь 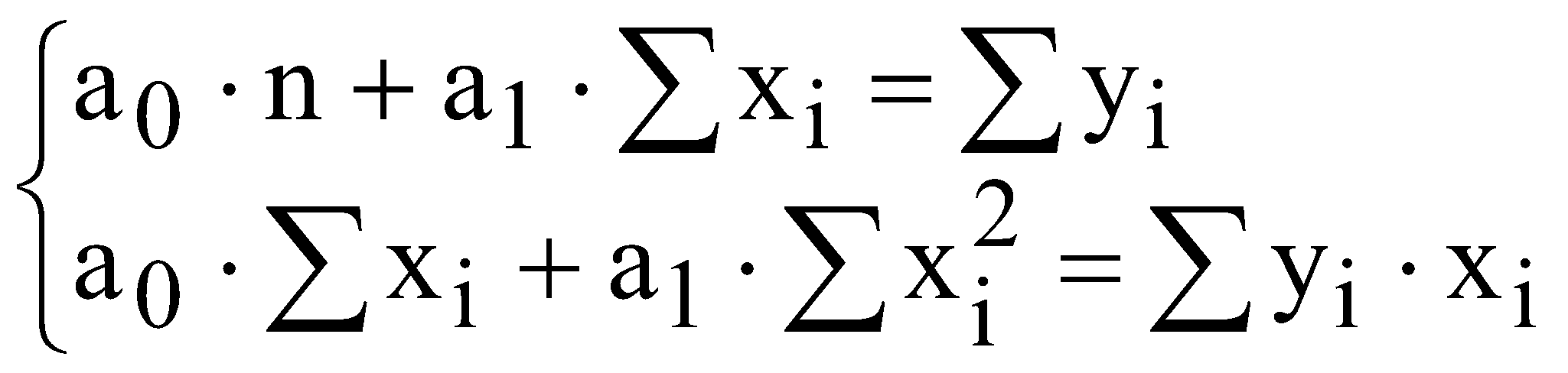 . (2.5) . (2.5)Невироджена система нормальних рівнянь має єдиний розв'язок, який можна знайти також за формулою де 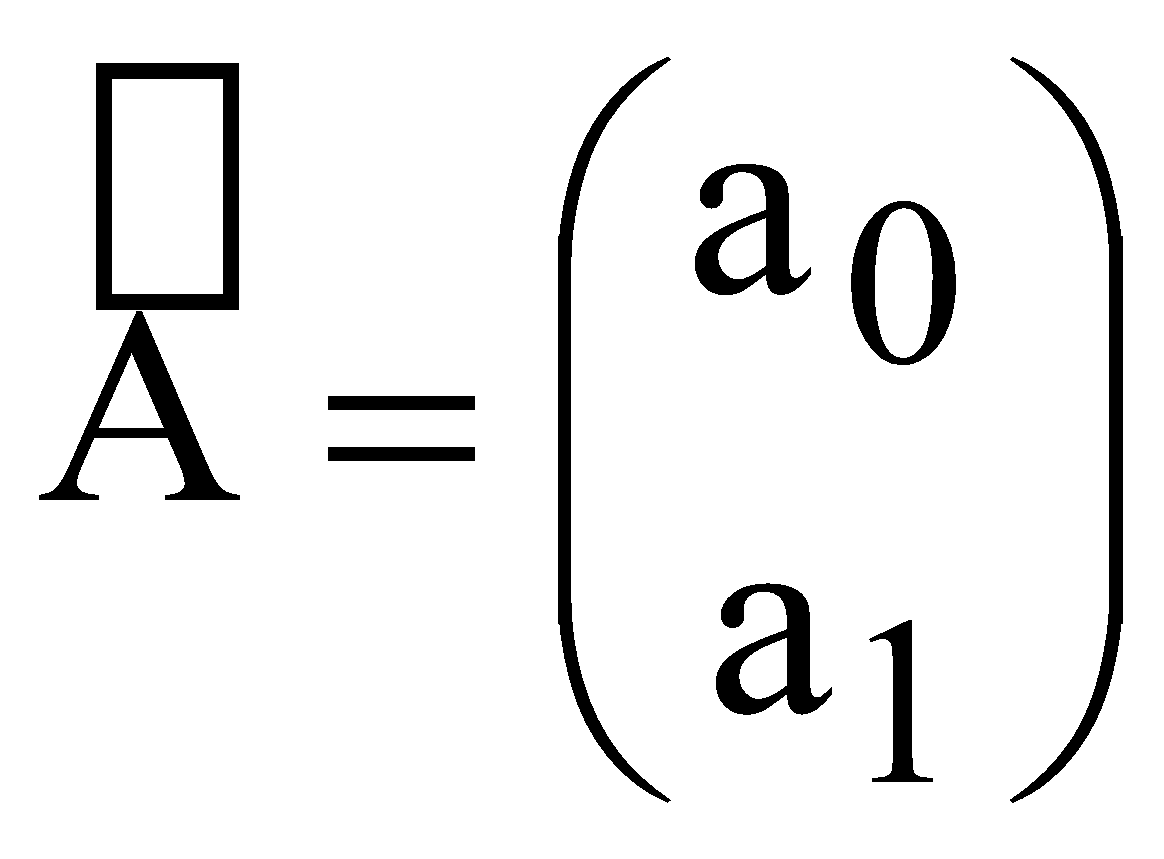 - вектор параметрів моделі; - вектор параметрів моделі;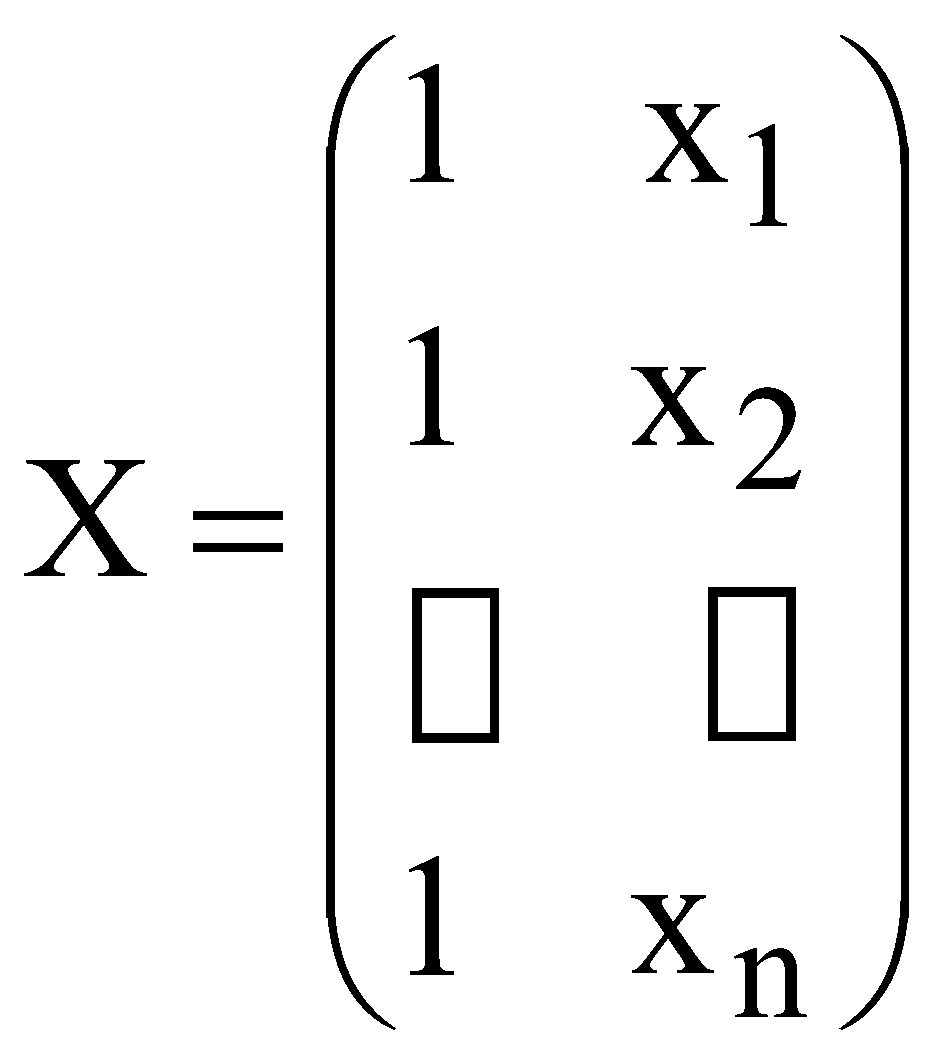 - матриця статистичних даних факторної ознаки; - матриця статистичних даних факторної ознаки;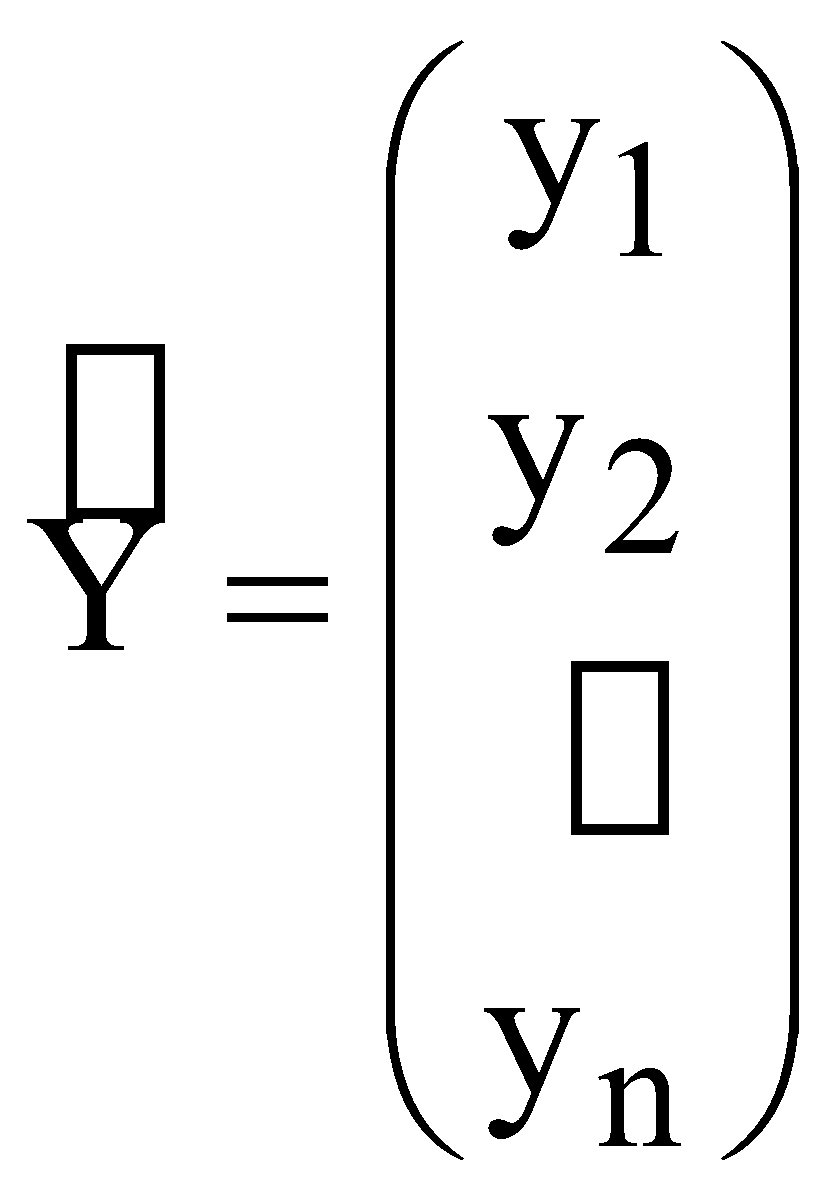 - вектор статистичних даних результуючої ознаки. - вектор статистичних даних результуючої ознаки.Щільність зв'язку між факторною і результативною ознаками можна знайти за допомогою коефіцієнта кореляції 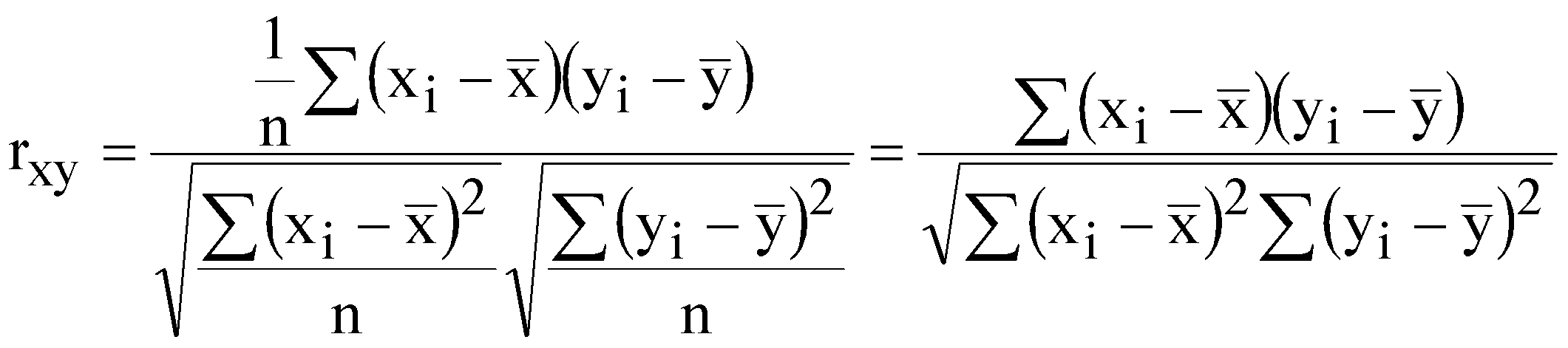 (2.7) (2.7)та коефіцієнта детермінації 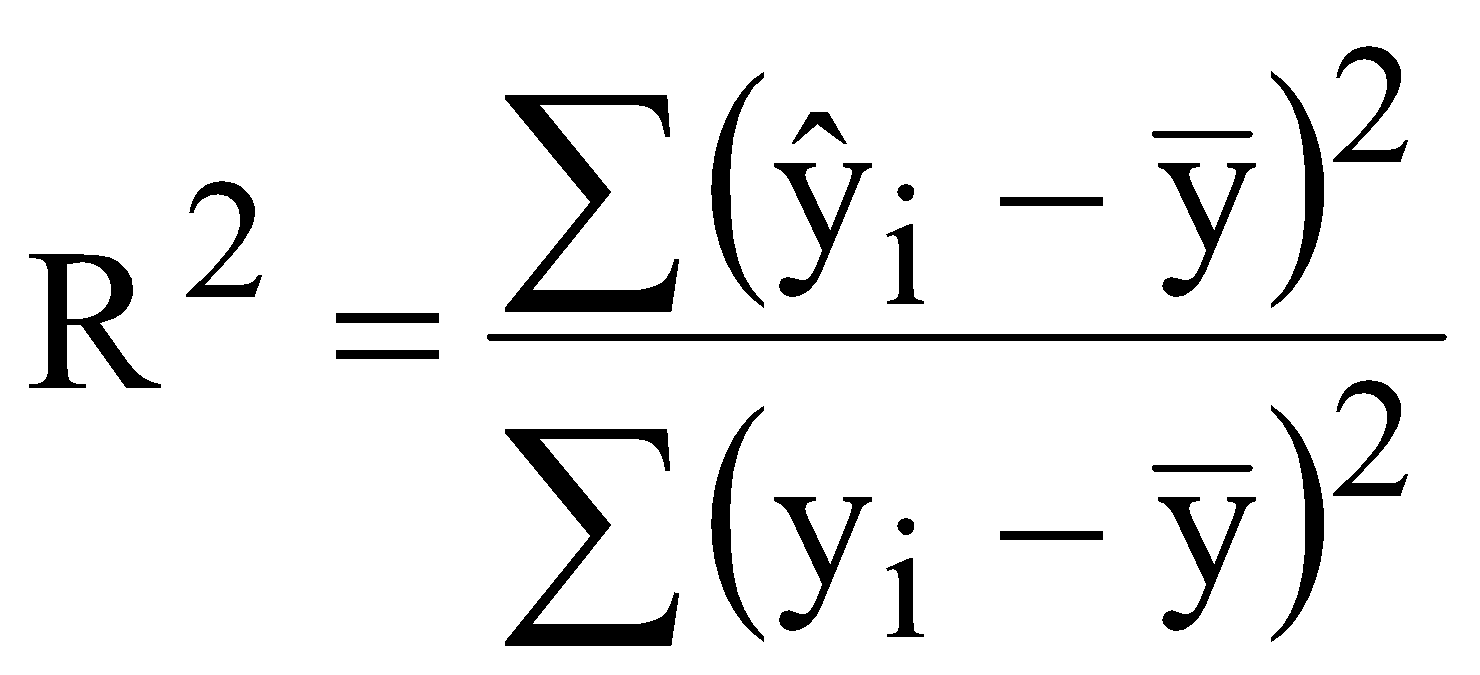 , (2.8) , (2.8)де Якщо Відповідь на питання про адекватність побудованої моделі може дати критерій Фішера (F-критерій). Для цього розраховується величина F 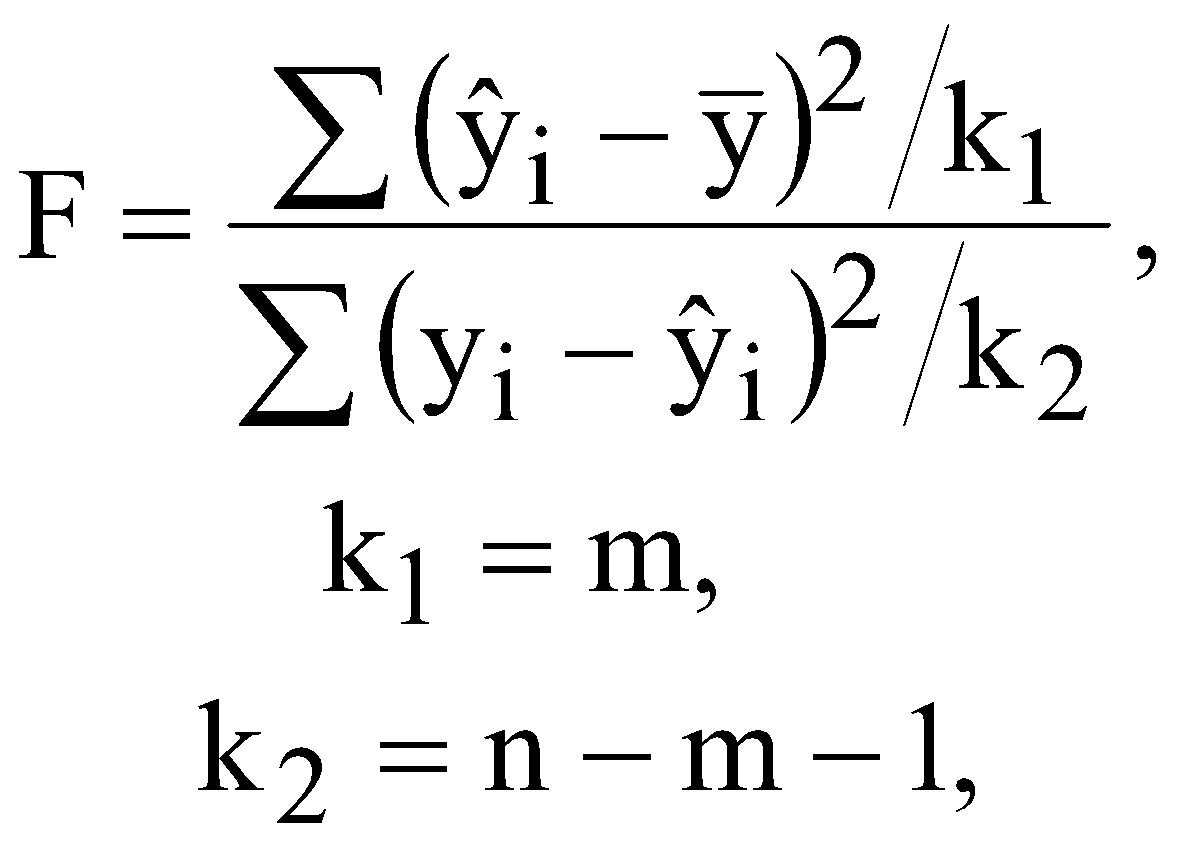 (2.9) (2.9)де m – кількість незалежних змінних; n - кількість спостережень. За статистичними таблицями F-розподілу з ступенями вільності k1 та k2 при заданому рівні ймовірності знаходимо значення Якщо встановлено, що із заданою ймовірністю економетрична модель адекватна спостережувальним даним і соціально-економічні умови за період прогнозування змінюються за закономірностями, що мають місце і в базовому періоді, то точкова оцінка прогнозу знаходиться за формулою Важливо також знайти інтервали довіри для прогнозу. Інтервали довіри – це інтервали, у які з певною заданою ймовірністю потрапляє дійсне значення залежної змінної. Такий інтервал довіри для прогнозного значення знаходимо за формулою де 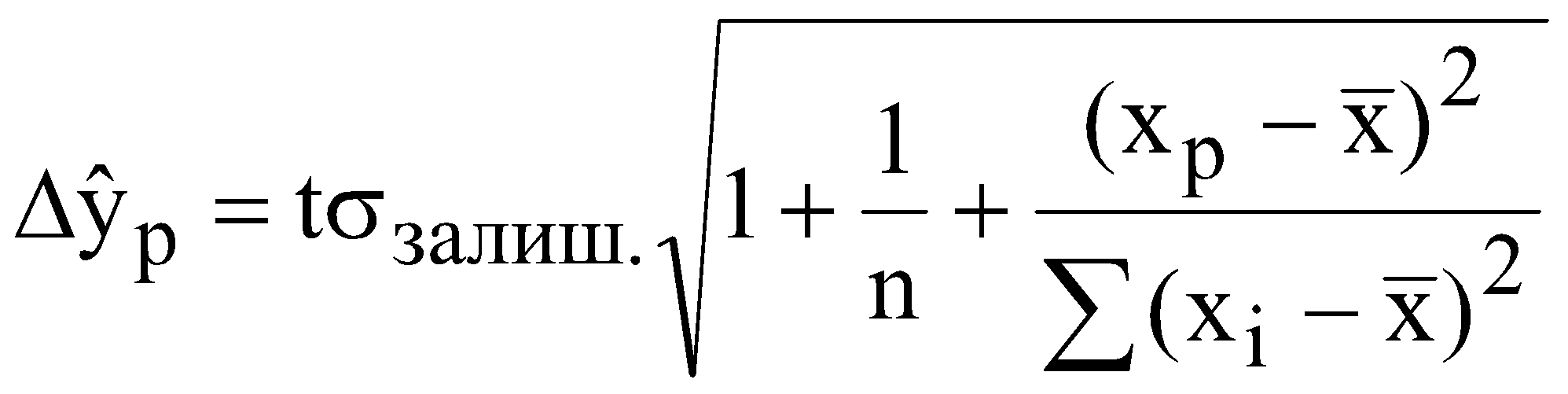 , (2.12) , (2.12)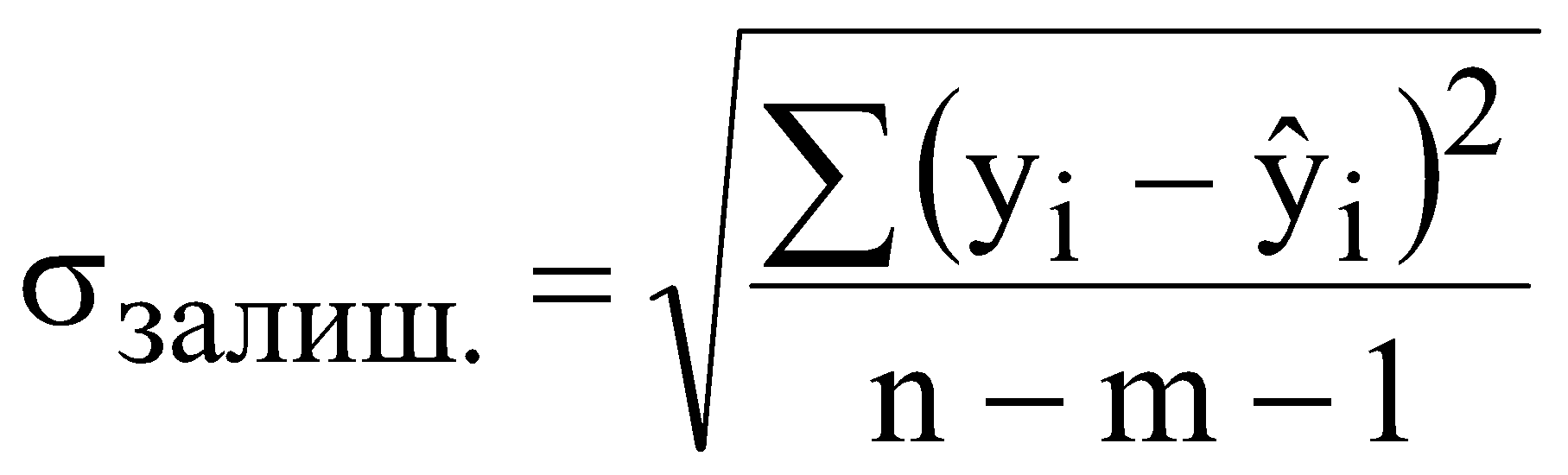 . (2.13) . (2.13)Для оцінки еластичності результуючої ознаки при будь-якому значенні факторної ознаки використовується коефіцієнт еластичності 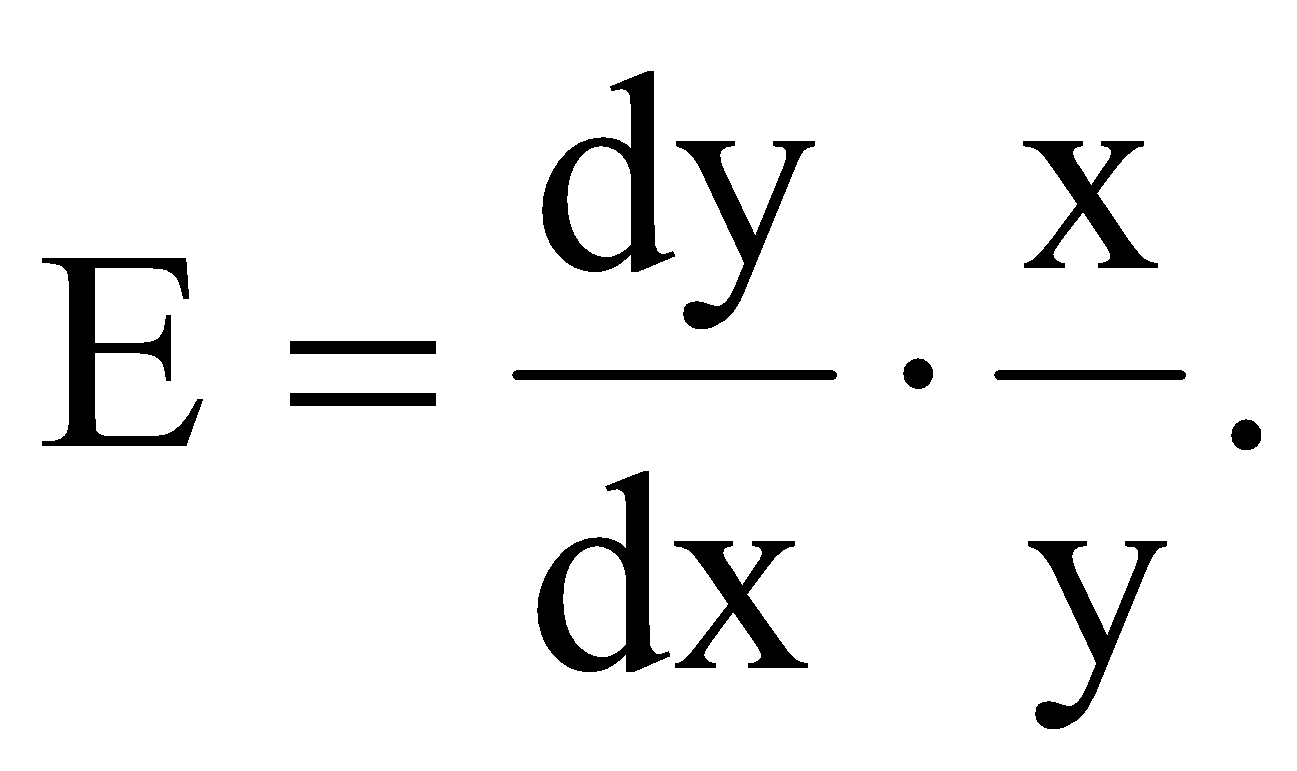 (2.14) (2.14)Коефіцієнт еластичності показує, на скільки відсотків зміниться показник, якщо фактор зміниться на 1%. ІІІ. Завдання За даними табл. 2.1 з ймовірністю 0,95 необхідно: Таблиця 2.1 Дані для побудови лінійної однофакторної моделі
побудувати однофакторну модель виду перевірити істотність зв'язку між факторами за допомогою коефіцієнта кореляції і коефіцієнта детермінації; оцінити надійність моделі за допомогою критерію Фішера; знайти прогнозне значення та інтервал довіри для прогнозу; визначити коефіцієнт еластичності в точці прогнозу; навести графічну інтерпретацію моделі. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
