Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb.
|
|
ЛАБОРАТОРНА РОБОТА №4 ПОБУДОВА ЛІНІЙНОЇ БАГАТОФАКТОРНОЇ МОДЕЛІ ТА ДОСЛІДЖЕННЯ ЇЇ АДЕКВАТНОСТІ І. Загальні положення Економічні явища змінюються під впливом багатьох факторів, які треба вміти виявити та оцінити. Наприклад, на обсяги збуту впливає якість продукції, ціна, імідж торгової марки, витрати на рекламу, доходи населення тощо. Багатофакторний регресійний аналіз допомагає знайти явний вигляд такої залежності та кількісно оцінити вплив різних факторів на досліджуваний процес. ІІ. Теоретичні відомості При побудові регресійного рівняння, де результуючий показник залежить від багатьох факторних ознак, слід включати в регресію всі фактори, які мають суттєвий вплив на показник y, а з другого боку необхідно визначати, чи виконується умова лінійної незалежності між факторами x1, x2,......,xn. Якщо між факторними ознаками існує лінійна залежність Хі=aХj, то говорять про те, що між цими факторами існує мультиколінеарність. Мультиколінеарність означає існування тісної лінійної залежності або сильної кореляції між двома або більше факторами. Вона негативно впливає на кількісні характеристики економетричної моделі або робить її побудову взагалі неможливою. Так як застосування методу найменших квадратів для оцінки параметрів регресійної залежності можливе лише при відсутності лінійної залежності між факторними величинами, то необхідно позбавитись цього явища. Це пов'язано з тим, що якщо має місце явище мультиколінеарності, неможливо отримати надійні оцінки параметрів МНК, тобто незначні зміни вибіркових даних приводять до значних змін оцінки параметрів. В економетричних задачах для дослідження наявності мультиколінеарності використовується метод Фаррара-Глобера. Цей алгоритм має три види статистичних критеріїв, згідно з якими перевіряється: мультиколінеарність усього масиву факторів (  -критерій); кожного фактора з іншими (F-критерій); кожної пари факторів (t-критерій).Для дослідження загальної мультиколінеарності і мультиколінеарності між окремими факторами використовується кореляційна матриця R і обернена до неї матриця Z 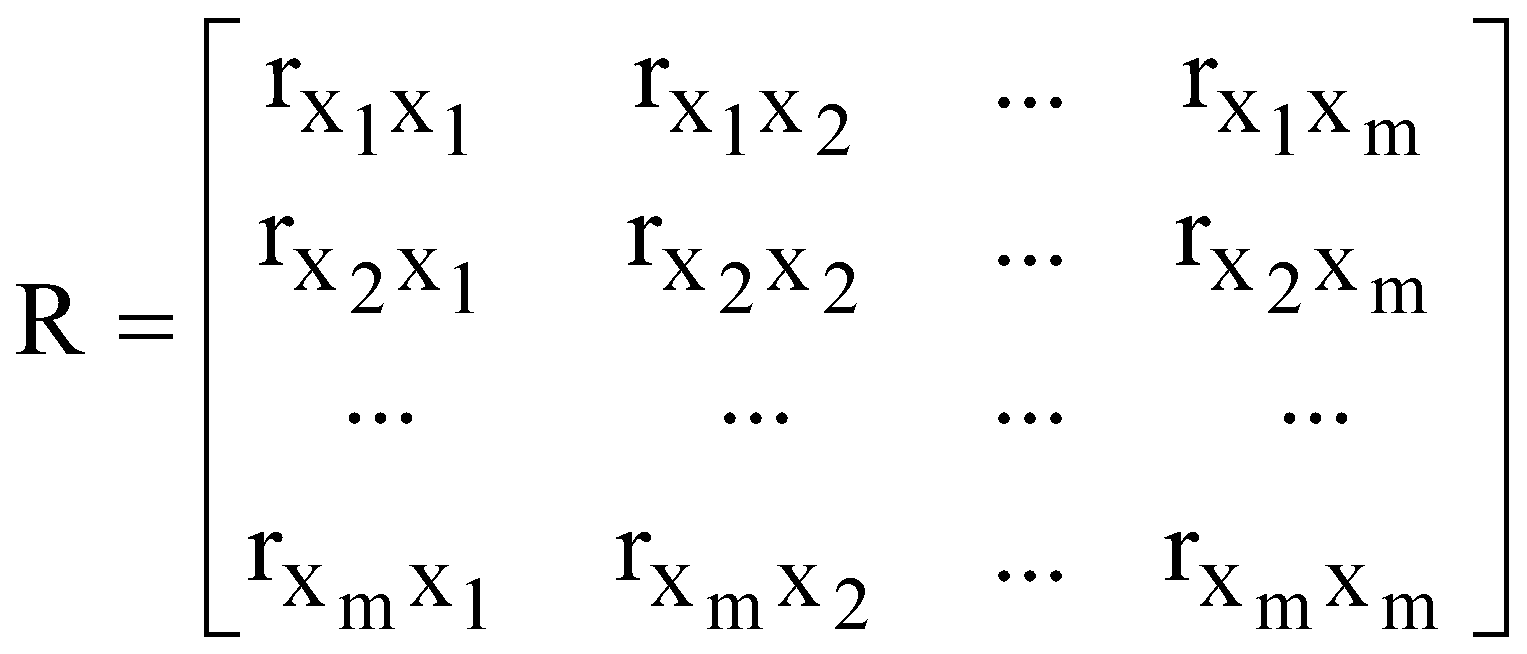 ,  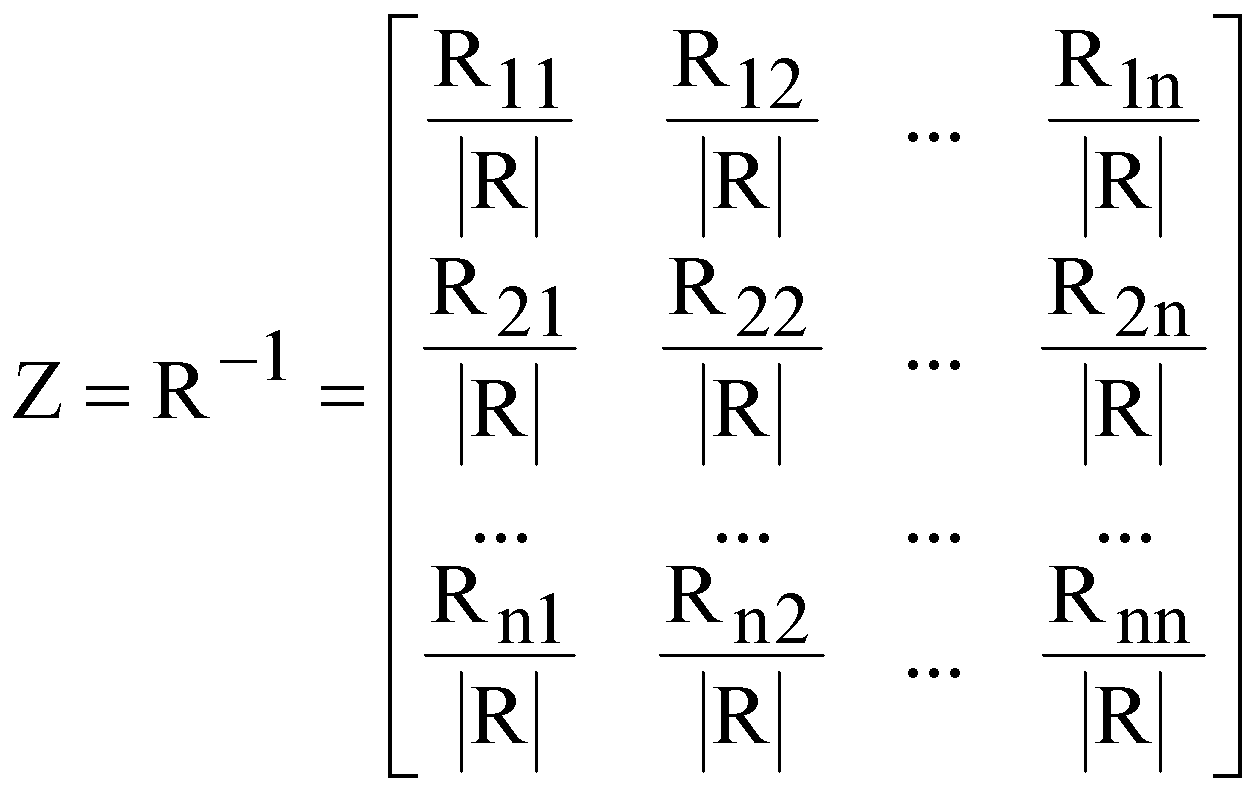, (4.1)де  - коефіцієнт кореляції, Rij – алгебраїчні доповнення до відповідних елементів матриці R.Для дослідження загальної мультиколінеарності використовується χ2-критерій. Для цього знаходимо визначник кореляційної матриці R і розраховуємо значення 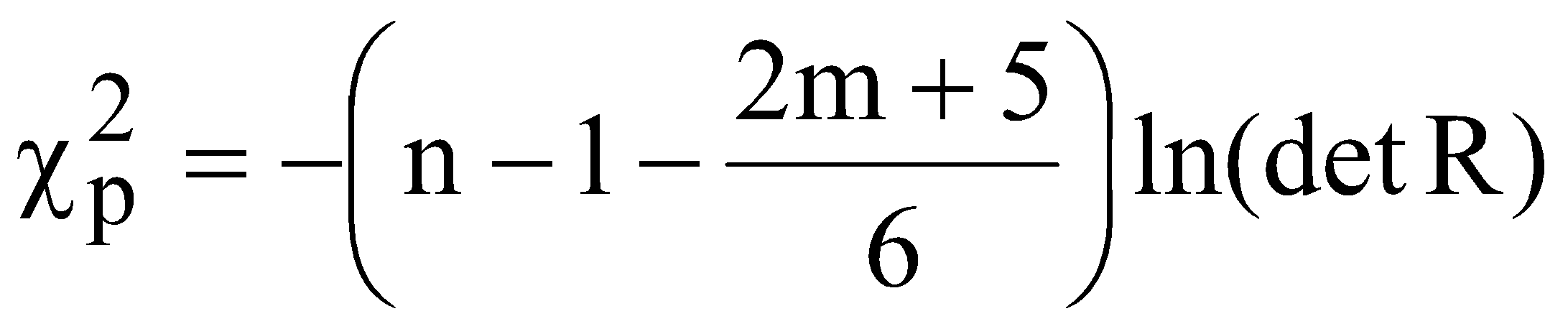 , (4.2)де n – кількість вибіркових значень, m – порядок кореляційної матриці, що розглядається (кількість факторів), det R – визначник матриці R. За заданою ймовірністю р і числом ступенів вільності  знаходимо табличне значення  . Якщо  , то із прийнятою надійністю можна вважати, що загальна мультиколінеарність відсутня. Якщо  , то із прийнятою ймовірністю можна вважати, що між факторами існує мультиколінеарність. Для з’ясування питання, між якими факторами існує мультиколінеарність, використовується F– або t–статистика. Обчислення F-критеріїв проводимо за формулою  , (4.3)де  - діагональні елементи Z.Фактичні значення критеріїв порівнюють з табличними при n-m-1 і m ступенях вільності і заданому рівні значущості  ( =1-р). Якщо  , то відповідний j-тий фактор мультиколінеарний з іншими.Для знаходження t–статистики між двома факторами спочатку знаходимо матрицю обернену до кореляційної, потім частинні коефіцієнти кореляції 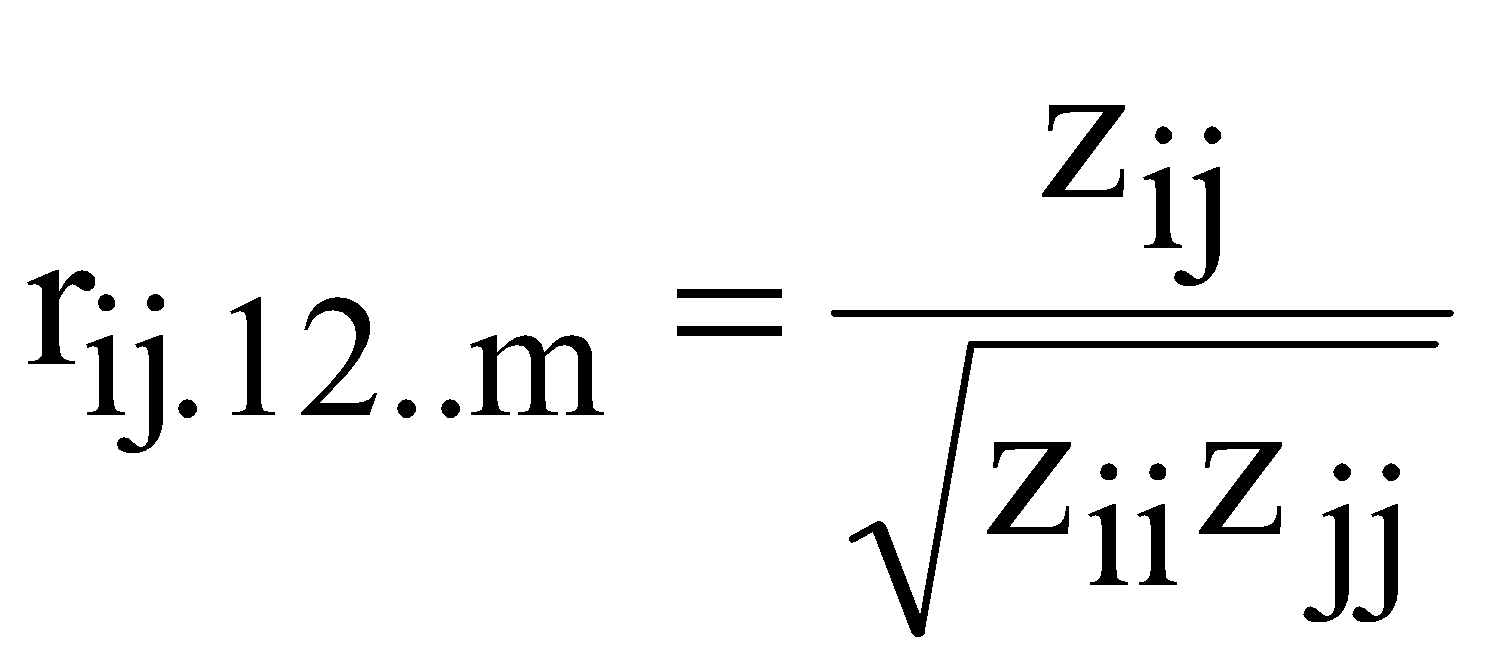 , (4.4)де  - елементи матриці Z. Частинні коефіцієнти кореляції характеризують тісноту зв'язку між двома факторами за умови, що інші фактори не впливають на цей зв'язок. Для цих частинних коефіцієнтів знаходиться t – статистика 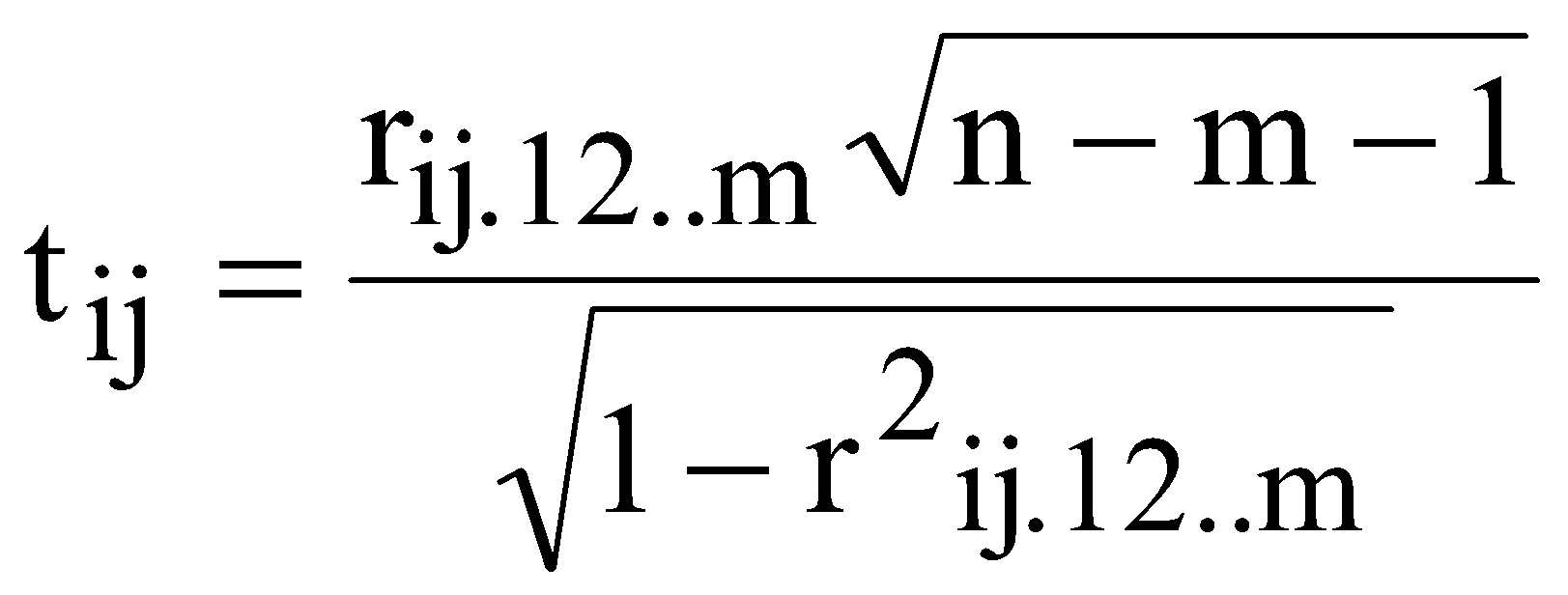 . (4.5)Для заданої ймовірності р і ступенів вільності k=n-m-1 знаходиться критичне значення критерію Стьюдента  . Якщо  , то з ймовірністю р можна стверджувати, що між факторами хі і xj існує мультиколінеарність.Для усунення мультиколінеарності потрібно замінити фактор xj на фактор  Якщо після заміни фактора має місце мультиколінеарність, то один із факторів виключають з розгляду. Заміна чи вилучення незалежних змінних завжди має узгоджуватись з економічною доцільністю, що випливає з мети дослідження. В загальному випадку багатофакторна лінійна регресія має вид  (4.6)де  - параметри моделі; - незалежні змінні;u – випадкові величини (відхилення). Оцінку параметрів 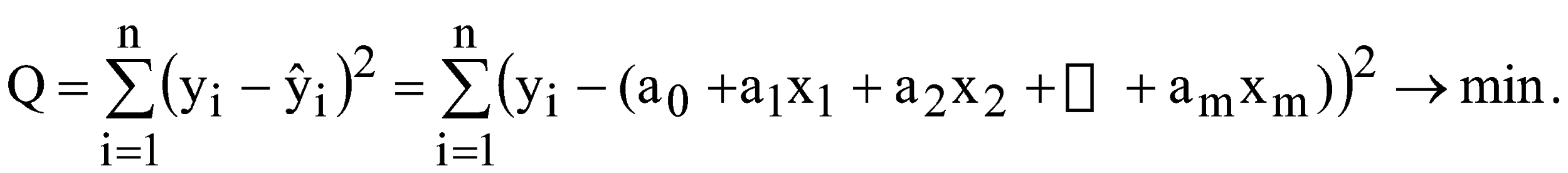знайдемо за допомогою МНК (4.7)Згідно з необхідною умовою екстремуму функції багатьох змінних у точках екстремуму 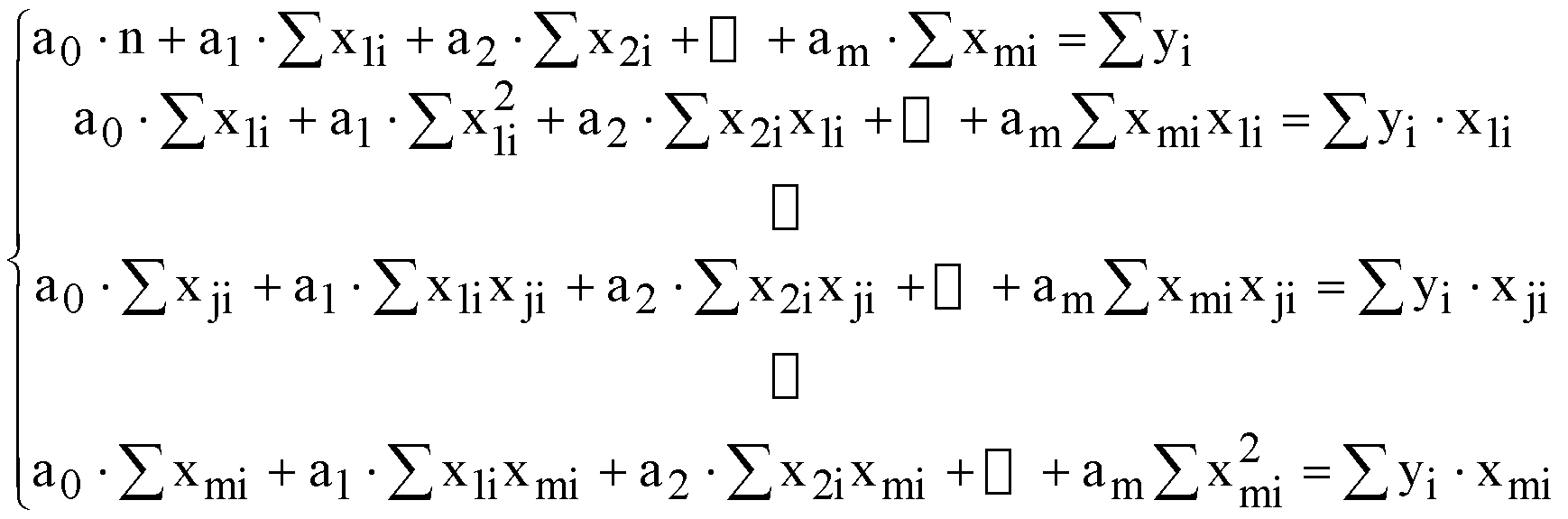частинні похідні дорівнюють нулю. Знаходячи частинні похідні та прирівнюючи їх до нуля, отримаємо . (4.8)Розв'язавши таку систему, отримаємо оцінки параметрів .Оцінки параметрів мо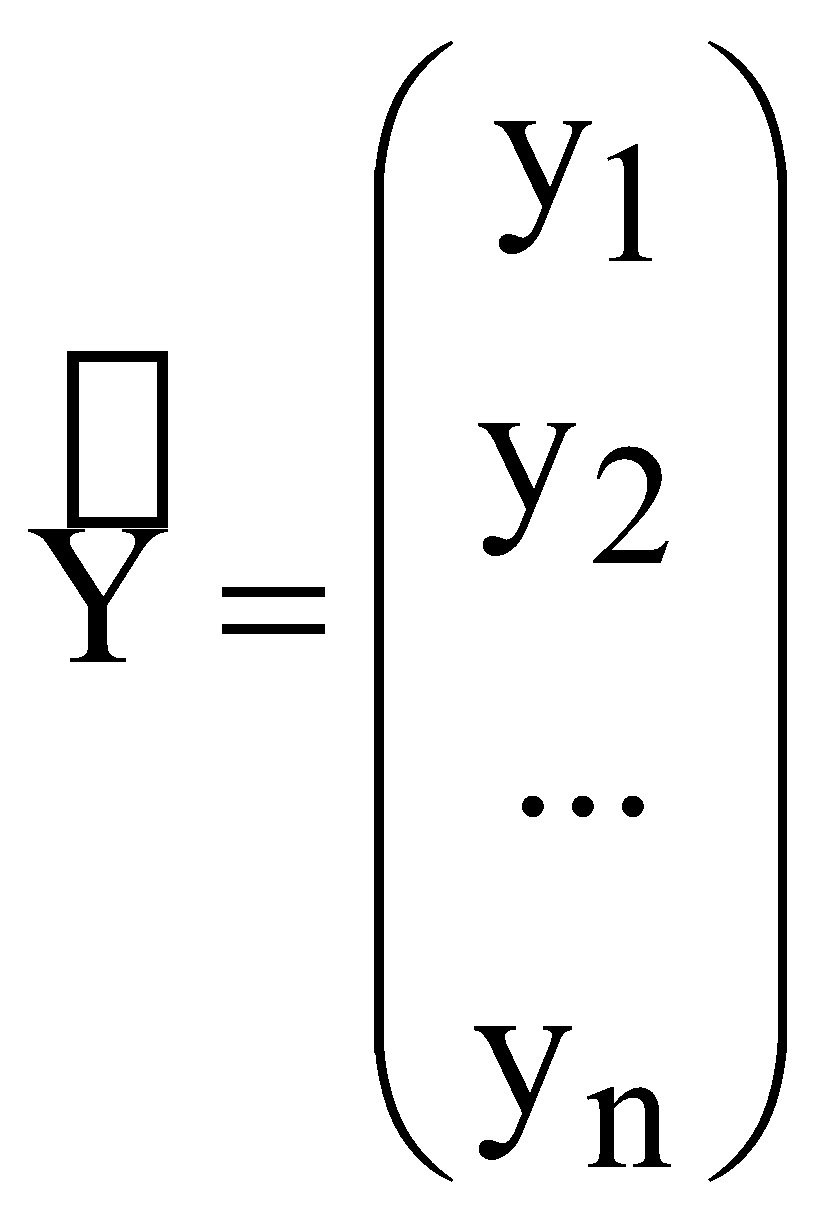жна знайти також за формулою , (4.9)де  - вектор спостережуваних даних показника; - матриця спостережуваних значень факторів хі,;х0 – фіктивний фактор, всі значення якого дорівнюють 1; 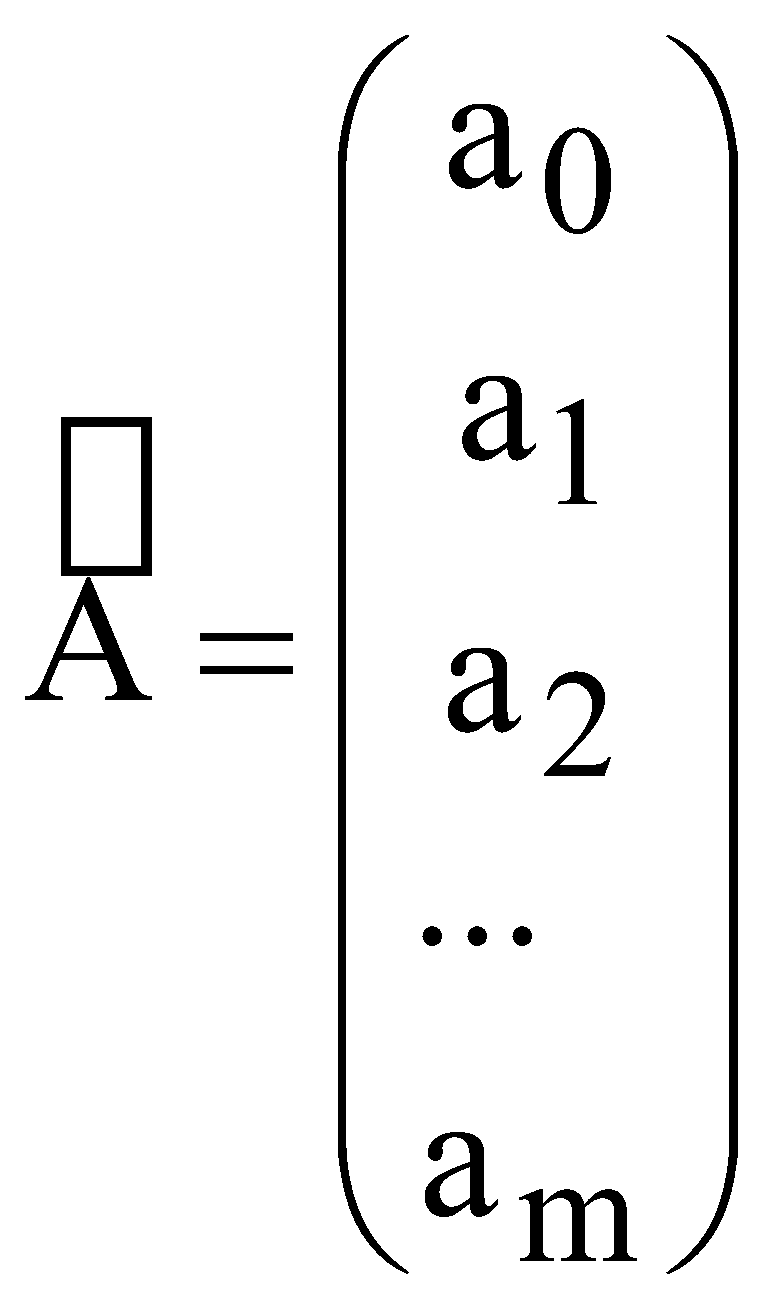 - вектор оцінюваних параметрів.Адекватність побудованої моделі статистичним даним генеральної сукупності можна перевірити за допомогою F-критерію (критерію Фішера) 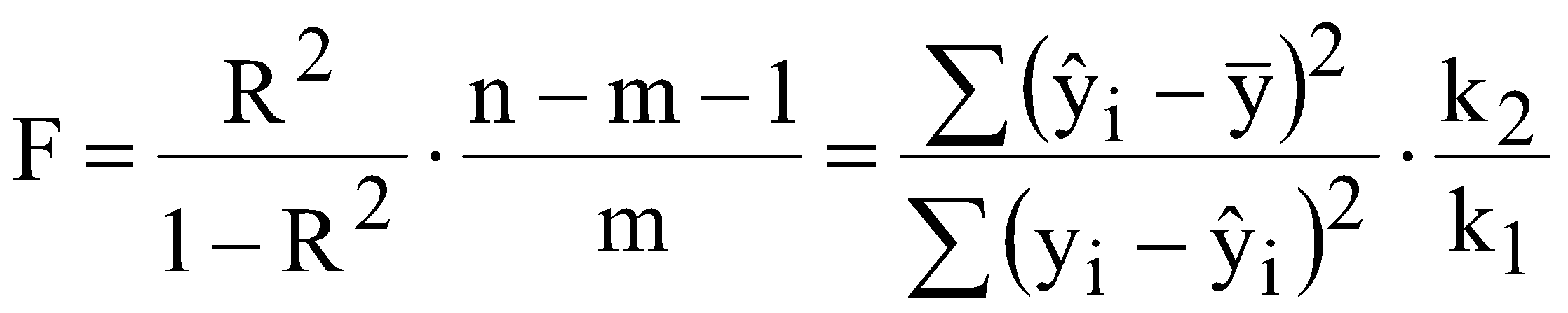 , (4.10)де  - коефіцієнт детермінації;n – кількість спостережень; m – незалежних змінних у рівнянні регресії;  - ступені вільності.Коефіцієнт множинної детермінації визначають за формулою 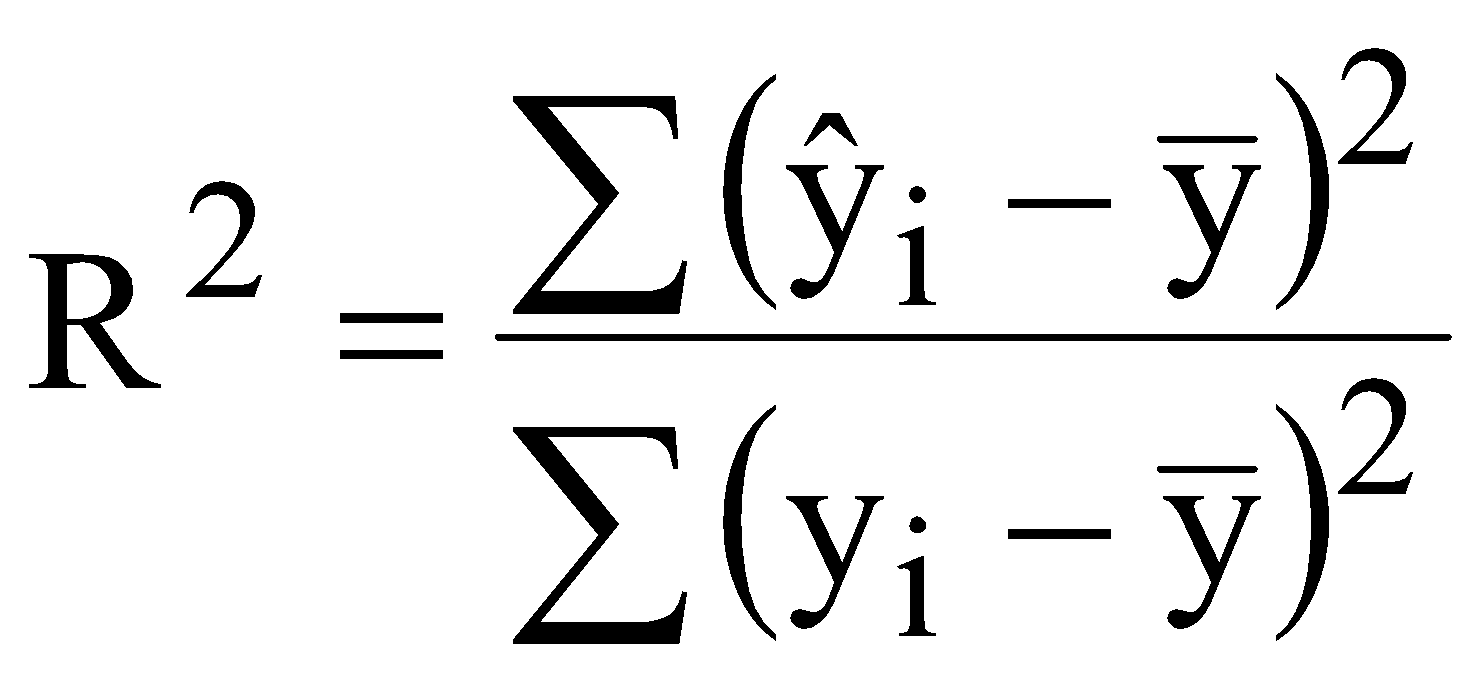 , (4.11)де  - фактичні значення показника; – теоретичні значення показника; – середнє значення.За статистичними таблицями з ступенями вільності  та рівнем ймовірності р знаходимо критичне значення Fкр. 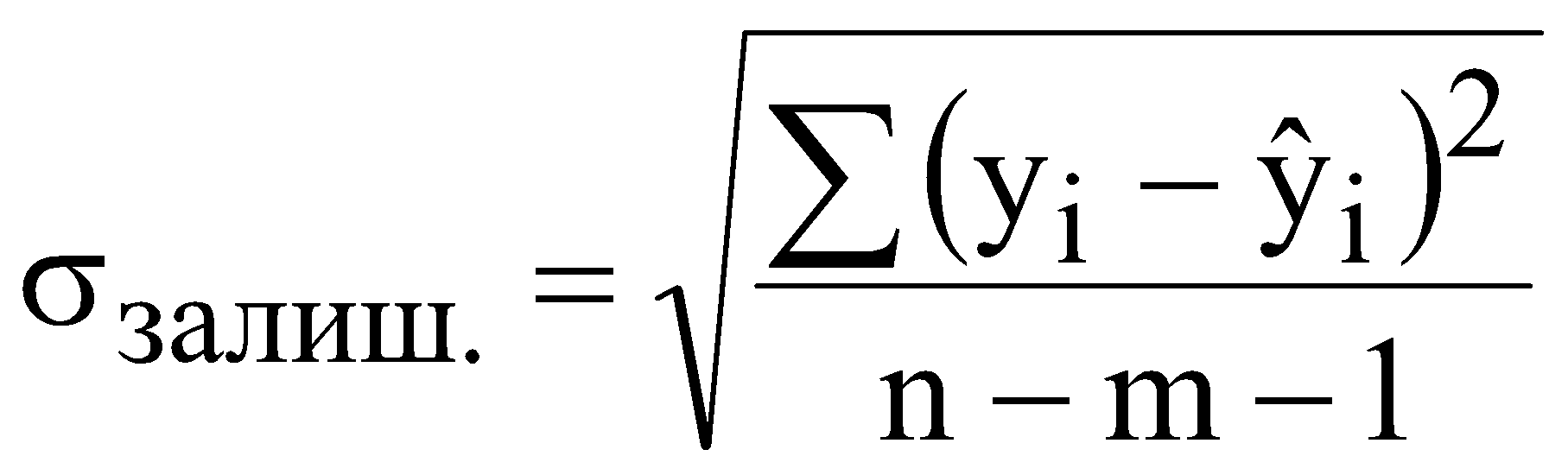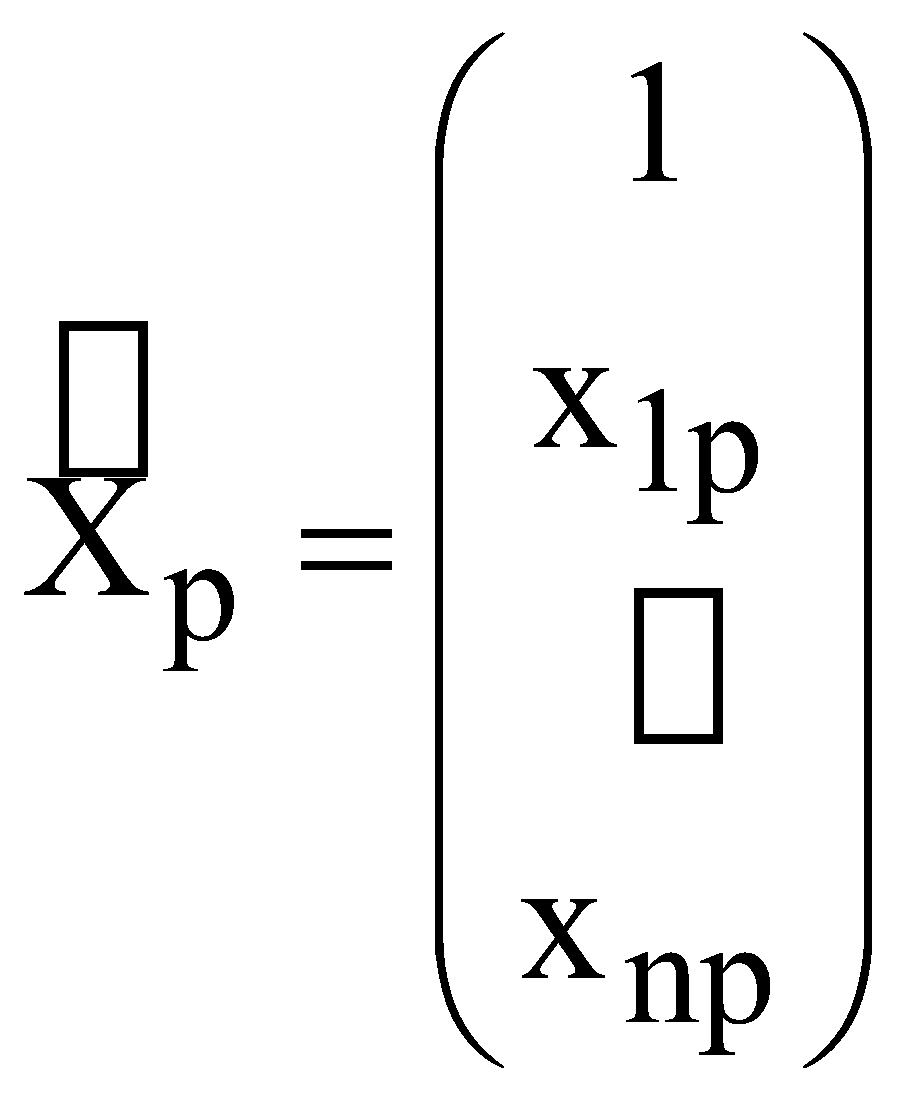Якщо F>Fкр, то побудована модель адекватна статистичним даним генеральної сукупності.Інтервал довіри для прогнозного значення знаходять за формулою  , (4.12) , (4.13)  , (4.14)де t – значення t-критерію при ймовірності р і n-m-1 ступенях вільності;  - середньоквадратичне відхилення залишків; - матриця спостережуваних значень факторів; - вектор прогнозних значень.Важливе значення для аналізу мають частинні коефіцієнти еластичності. Для багатофакторної регресії частинний коефіцієнт еластичності показує, на скільки відсотків зміниться показник, якщо один із факторів зміниться на один відсоток при незмінних значеннях інших факторів. Частинний коефіцієнт еластичності для фактора 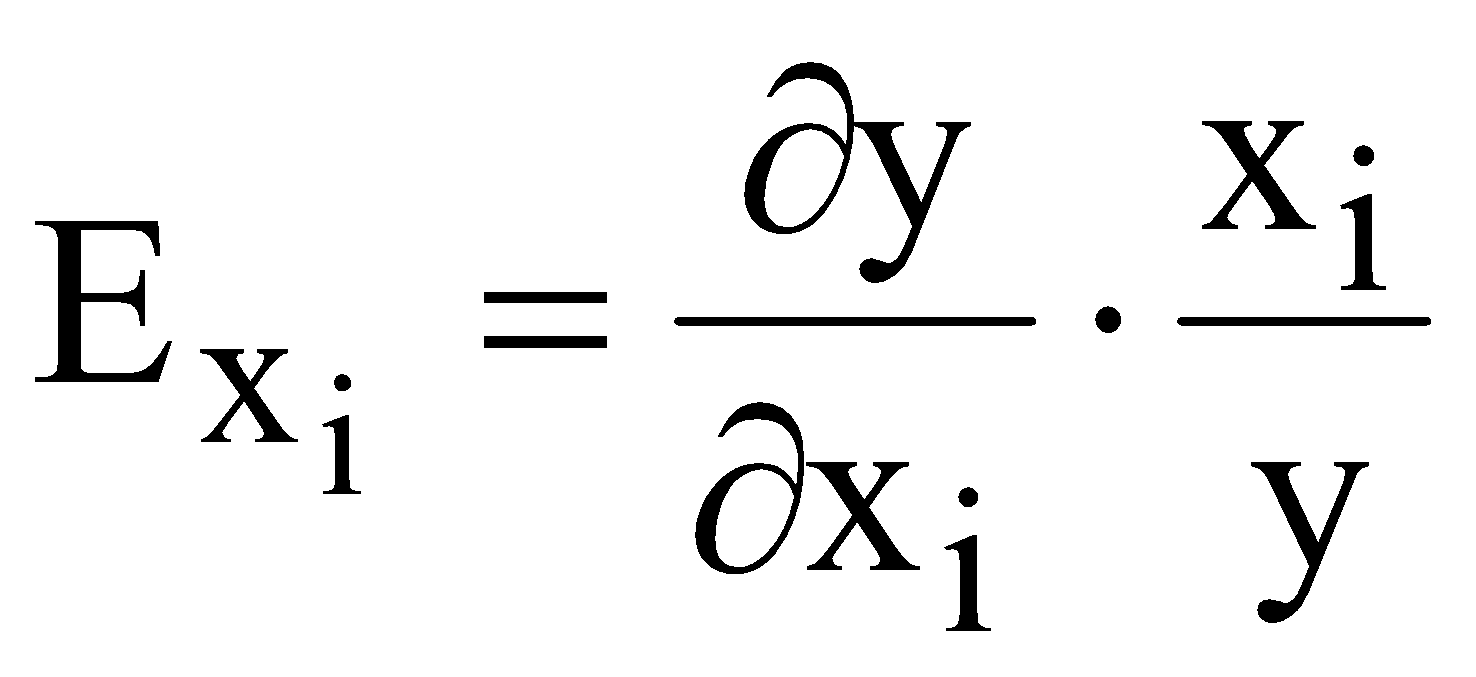 обчислюється за формулою (4.15)Частинний коефіцієнт еластичності показує, як змінюється показник у, якщо фактор  змінюється на 1 % при незмінних значеннях інших факторів. Аналогічно отримаємо для коефіцієнт еластичності інших факторів. |