Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb. Скачать 3.77 Mb.
|
|
(6.16) де Якщо встановлено, що із заданою ймовірністю економетрична модель адекватна статистичним даним генеральної сукупності та при умові, що тенденції розвитку економічного процесу не змінилися, то точкова оцінка прогнозу знаходиться за формулою Важливо також знайти інтервали довіри. Інтервали довіри – це інтервали, у які з певною заданою ймовірністю потрапляє дійсне значення залежної змінної. Такий інтервал довіри для прогнозного значення знаходимо за формулою де 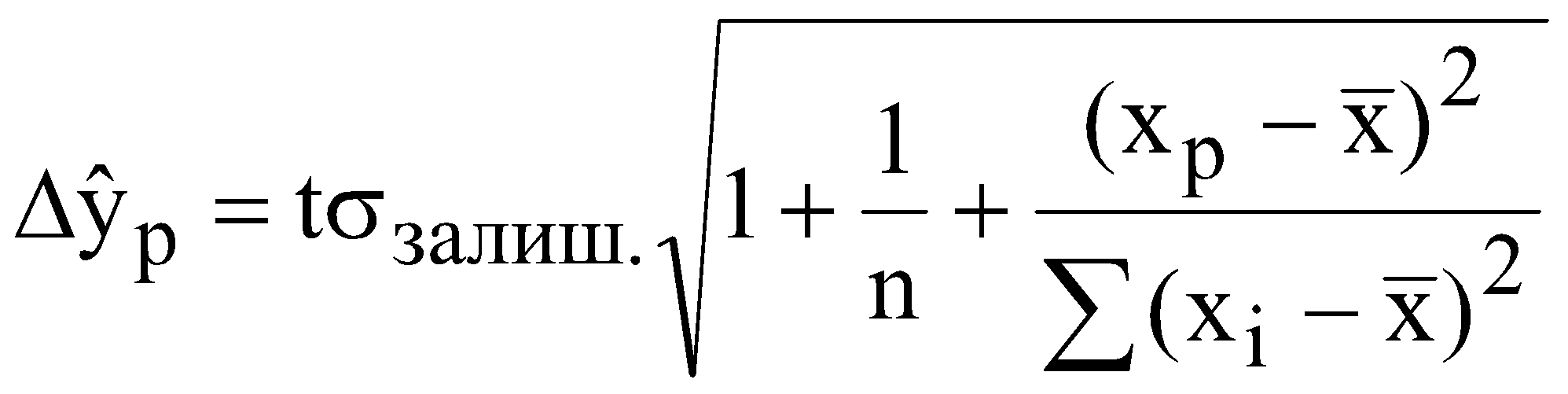 , (6.19) , (6.19)Для оцінки еластичності результуючої ознаки при будь-якому значенні факторної ознаки використовується коефіцієнт еластичності: 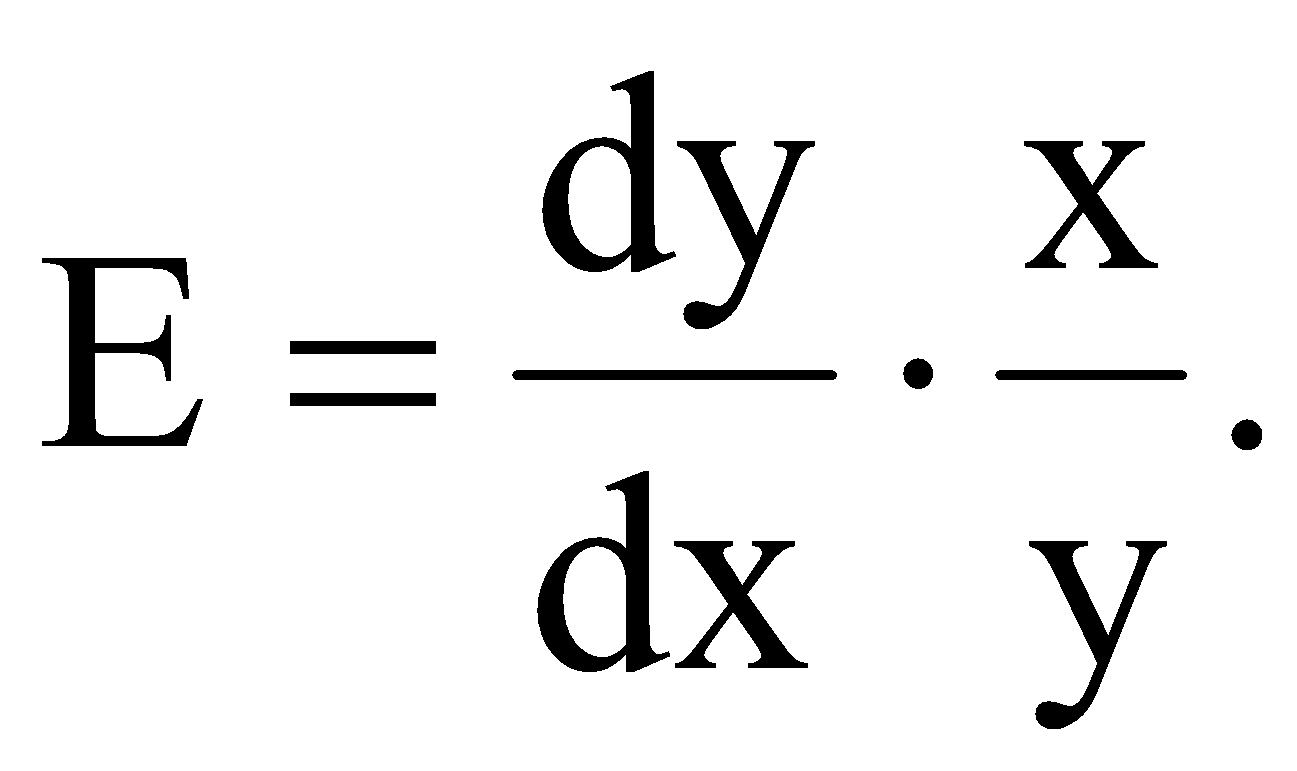 (6.20) (6.20)ІІІ. Завдання За даними табл. 6.1 з ймовірністю 0,95, використовуючи метод Койка, необхідно: Таблиця 6.1 Дані для побудови лагової моделі
оцінити параметри лагової моделі; оцінити адекватність побудованої моделі статистичним даним генеральної сукупності за допомогою критерію Фішера і Дарбіна-Уотсона; визначити прогнозне значення та інтервал довіри для прогнозу; визначити коефіцієнт еластичності для прогнозу. ЛАБОРАТОРНА РОБОТА №7 ПРИЙНЯТТЯ РІШЕНЬ В УМОВАХ ПОВНОЇ НЕВИЗНАЧЕНОСТІ І. Загальні положення Прийняття рішення (стратегії) серед кількох варіантів в умовах визначеності характеризується однозначною, детермінованою залежністю прийнятого рішення від ряду властивостей стратегії (від вектора властивостей, ознак або якостей), які враховуються для кожного варіанту можливого рішення. Складнішим є формування критеріїв в умовах невизначеності. Одним із визначальних факторів у таких задачах є зовнішнє середовище, або природа. ІІ. Теоретичні відомості У загальному випадку природа (зовнішнє середовище) може знаходитися в одному зі станів П1, П2, ...., Пn. Ймовірність знаходження у цих станах є невідомою для особи, що приймає рішення. В іграх з природою, як і в стратегічних іграх, створення моделі повинно починатися з побудови платіжної матриці. Припустимо, що гравець А має m можливих стратегій (А1, А2, …, Аm), а природа П може знаходитися в одному з станів n (П1, П2, ..., Пn), які можна розглядати як її "стратегії". Сукупність (П1, П2, ..., Пn) формується або на основі досвіду аналізу станів природи, або в результаті передбачень та інтуїції експертів, тобто використання експертних оцінок. Виграш гравця А за умов вибраної ним стратегії Aі (і = 1, …, m) та станів Пj (j = 1 ,..., n) природи П позначимо аij (і = 1, …, m; j = 1 ,..., n). З виграшів гравця А формують платіжну матрицю А (табл. 7.1). Таблиця 7.1 Платіжна матриця А
Методи прийняття рішень в іграх з природою залежать від того, відомі чи ні ймовірності станів природи, тобто має місце ситуація повної невизначеності. Для прийняття рішень в умовах повної невизначеності використовуються наступні критерії: критерій Лапласа; критерій Вальда; критерій Севіджа; критерій Гурвіца. 1. Критерій Лапласа. Критерій Лапласа спирається на принцип недостатнього підґрунтя, виходячи з якого, всі стани природи Пj є рівноймовірними. Відповідно до цього принципу кожному стану Пj відповідає ймовірність рj, яка визначається за формулою Для прийняття рішень для кожної стратегії Aі розраховується середнє арифметичне значення виграшу 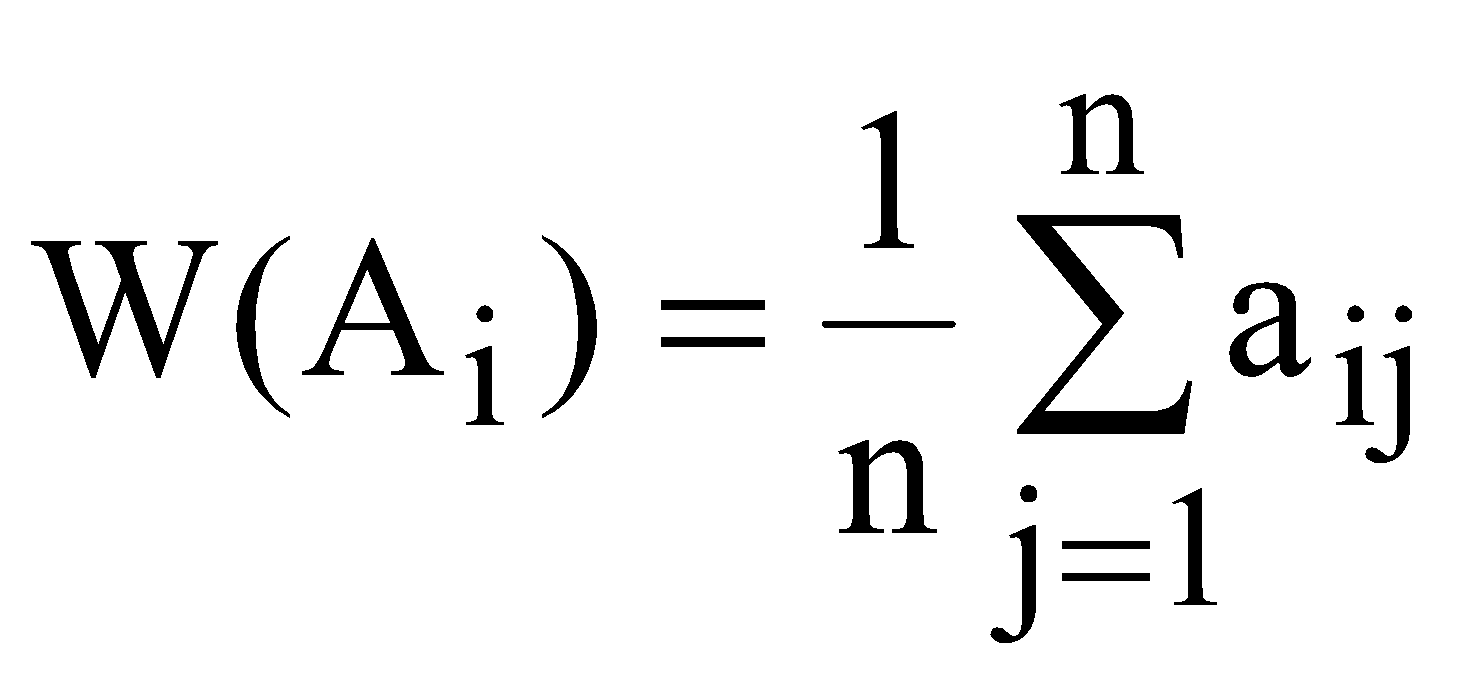 . (7.2) . (7.2)Серед 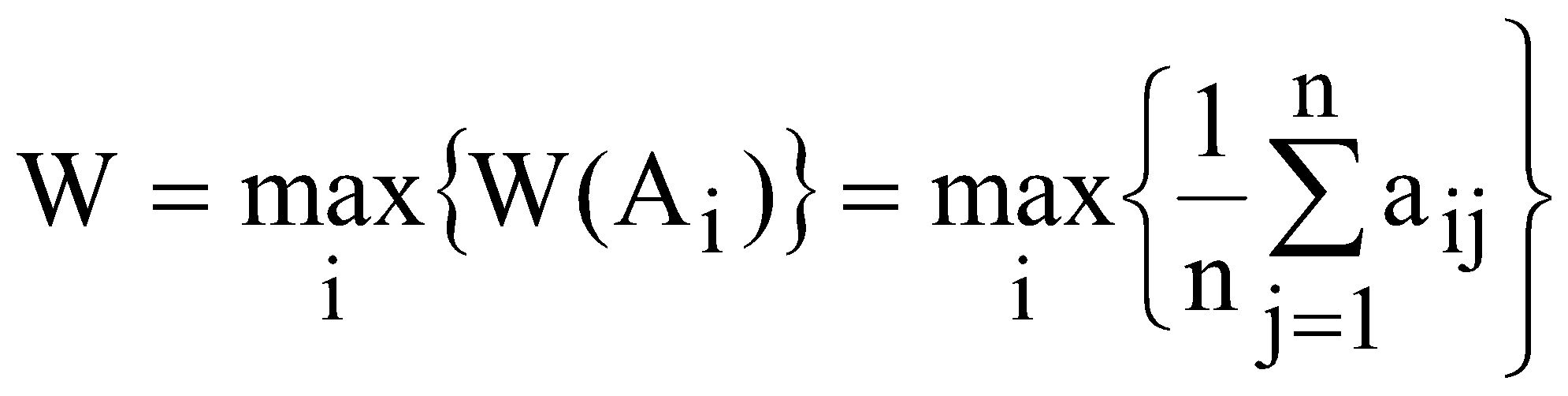 . (7.3) . (7.3)2. Критерій Вальда. Критерій Вальда – це критерій гарантованого результату. Він базується на принципі найбільшої обережності, оскільки вибирають найкращу із найгірших стратегій Аі. Якщо елементи платіжної матриці аij характеризують виграш (корисність), то для визначення оптимальної стратегії використовується максимінний критерій. Для цього у кожному рядку матриці виграшів знаходять найменший елемент 3. Критерій Севіджа |
