Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb. Скачать 3.77 Mb.
|
|
ІІІ. Завдання За статистичними даними (табл. 4.1) необхідно: Таблиця 4.1 Дані для побудови багатофакторної моделі
побудувати кореляційну матрицю; використовуючи χ2-критерій з ймовірністю 0,95 оцінити наявність загальної мультиколінеарності; якщо існує загальна мультиколінеарність, то використовуючи t-статистику з р=0,95 виявити пари факторів, між якими існує мультиколінеарність. Якщо такі пари існують, то один із факторів необхідно вилучити; знайти оцінки параметрів багатофакторної регресії; оцінити щільність зв’язку між результативною і факторними ознаками за допомогою коефіцієнта детермінації; перевірити адекватність побудованої моделі за допомогою критерію Фішера; знайти прогнозне значення (y16) та інтервали довіри для прогнозу; визначити частинні коефіцієнти еластичності для прогнозу. ЛАБОРАТОРНА РОБОТА №5 ВИЗНАЧЕННЯ ГЕТЕРОСКЕДАСТИЧНОСТІ ТА АВТОКОРЕЛЯЦІЇ ЗАЛИШКІВ І. Загальні положення Передумови застосування МНК, які складають основу класичного регресійного аналізу, на практиці часто порушуються. В таких випадках виникають явища гетероскедастичності та автокореляції. Ці явища призводять до неадекватності побудованої моделі. ІІ. Теоретичні відомості Однією із передумов застосування МНК є стала величина дисперсії залишків для всіх спостережень. Така властивість називається гомоскедастичністю. У практичних дослідженнях часто порушується умова гомоскедастичності, тобто існує явище гетероскедастичності. Якщо існує герескедастичність залишків, то це призводить до того, що оцінки параметрів економетричної моделі, знайдені за допомогою методу найменших квадратів, будуть незміщеними, обґрунтованими, але неефективними. Одним із методів перевірки припущень про наявність гетероскедастичності є метод на основі критерію Вихідні дані залежної змінної Y розбиваються на k груп відповідно до зміни рівня величини Y. За кожною групою даних обчислюється сума квадратів відхилень ( 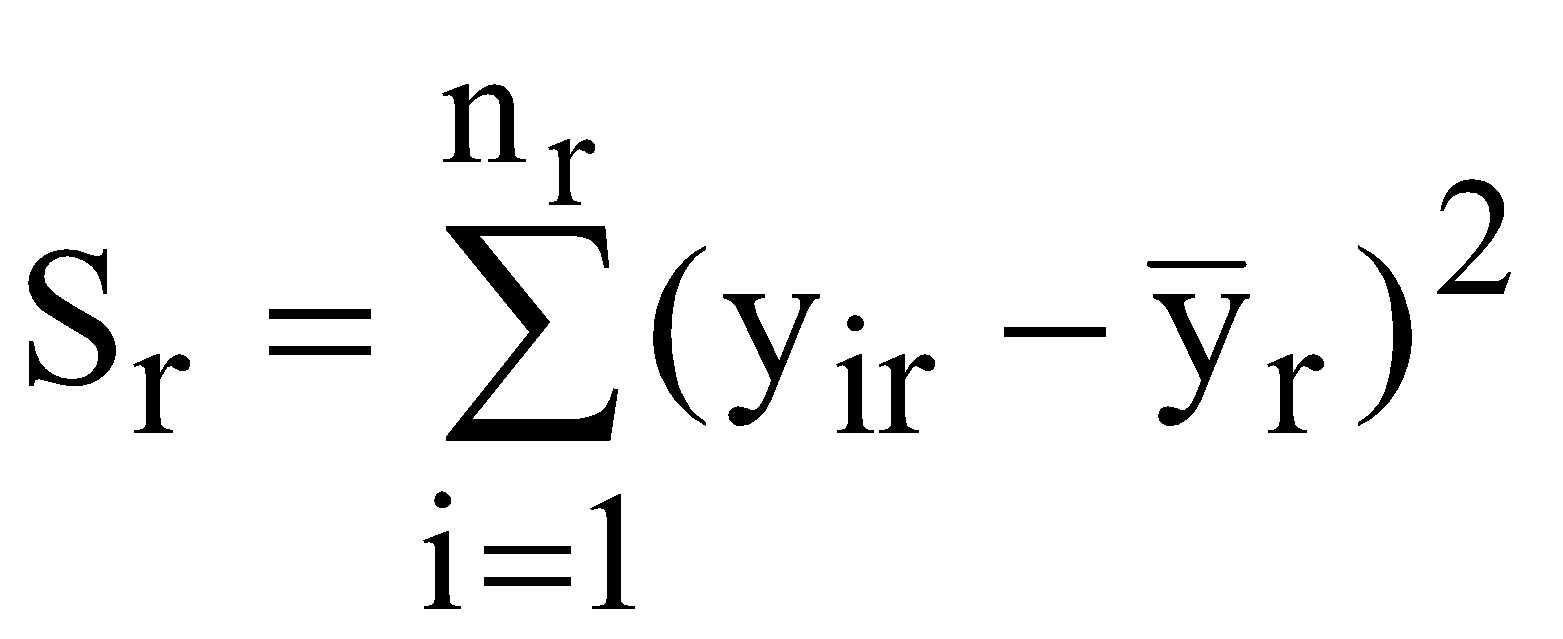 . (5.1) . (5.1)Визначається сума квадратів відхилень загалом по всій сукупності спостережень 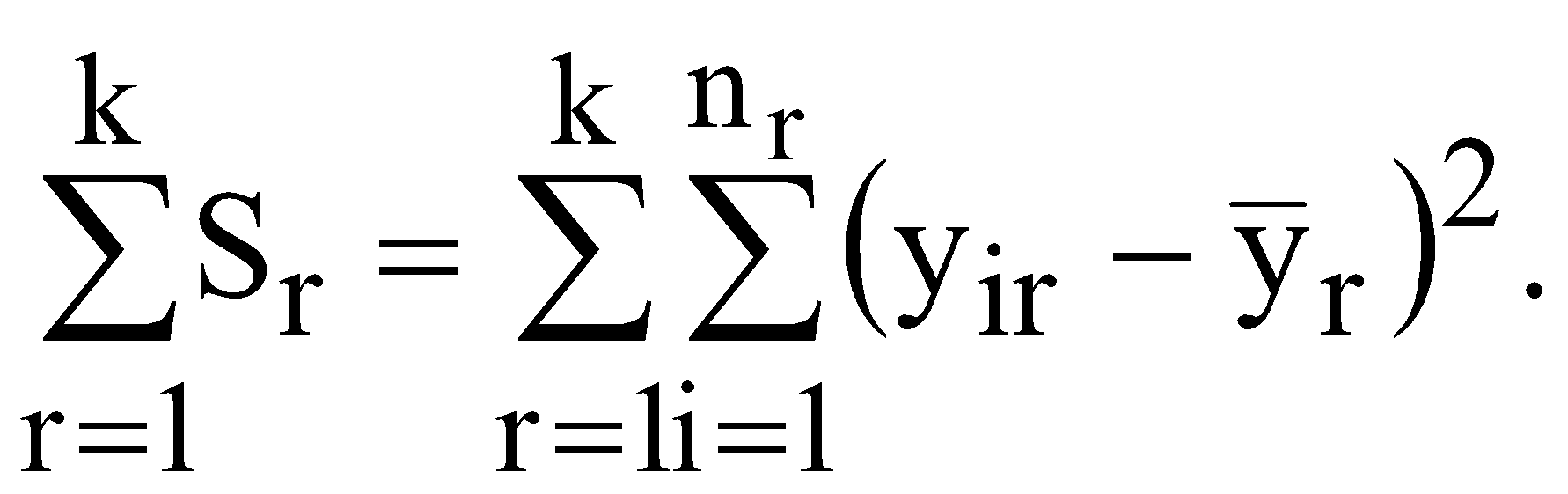 (5.2) (5.2)Обчислюється параметр 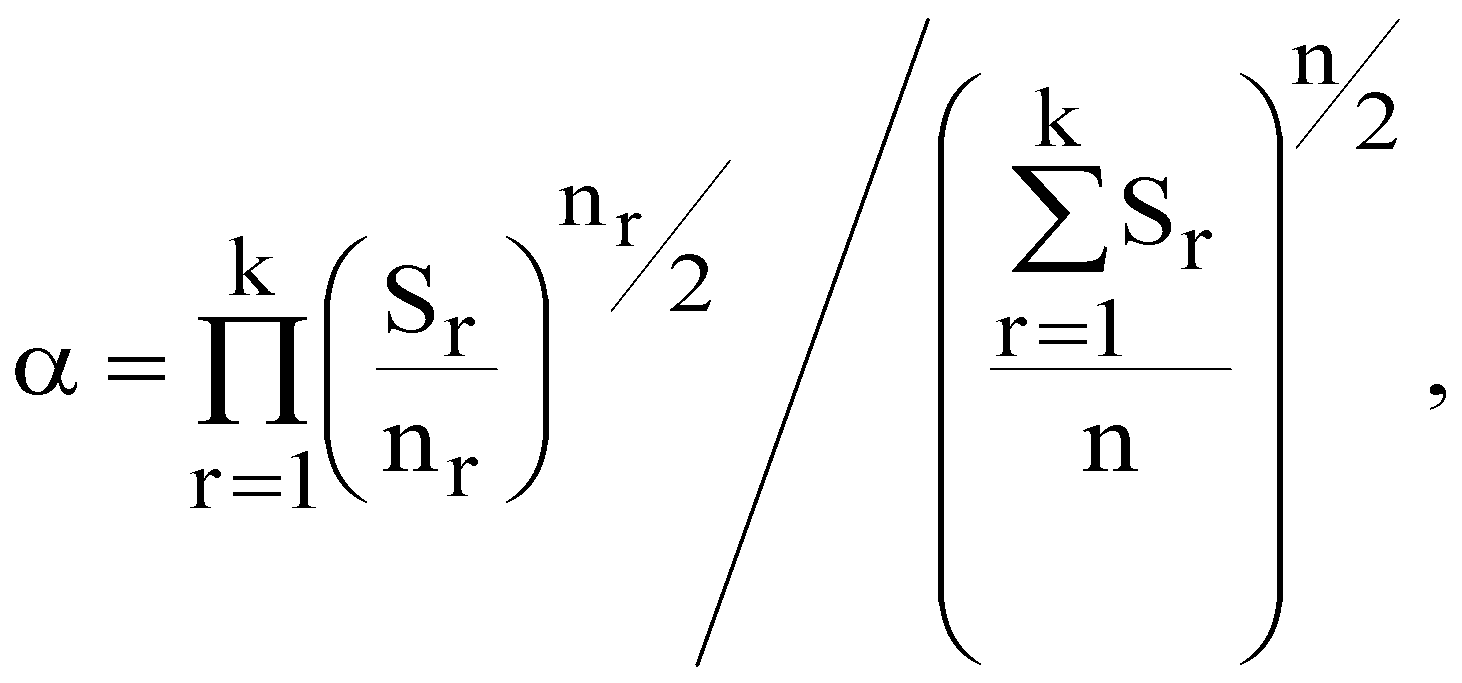 (5.3) (5.3)де n – загальна сукупність спостережень; nr – кількість спостережень r-ї групи. Обчислюється критерій який наближено дорівнюватиме розподілу Для побудови економетричної моделі використаємо метод найменших квадратів (МНК). Математично 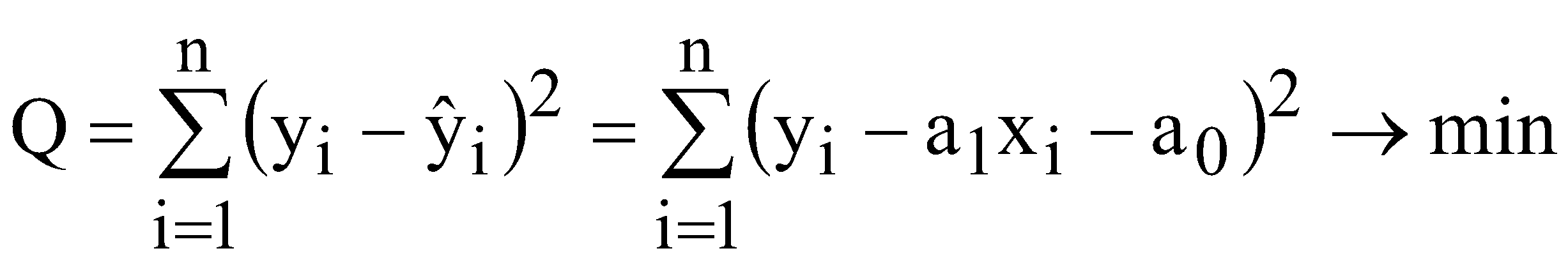 . (5.6) . (5.6)де 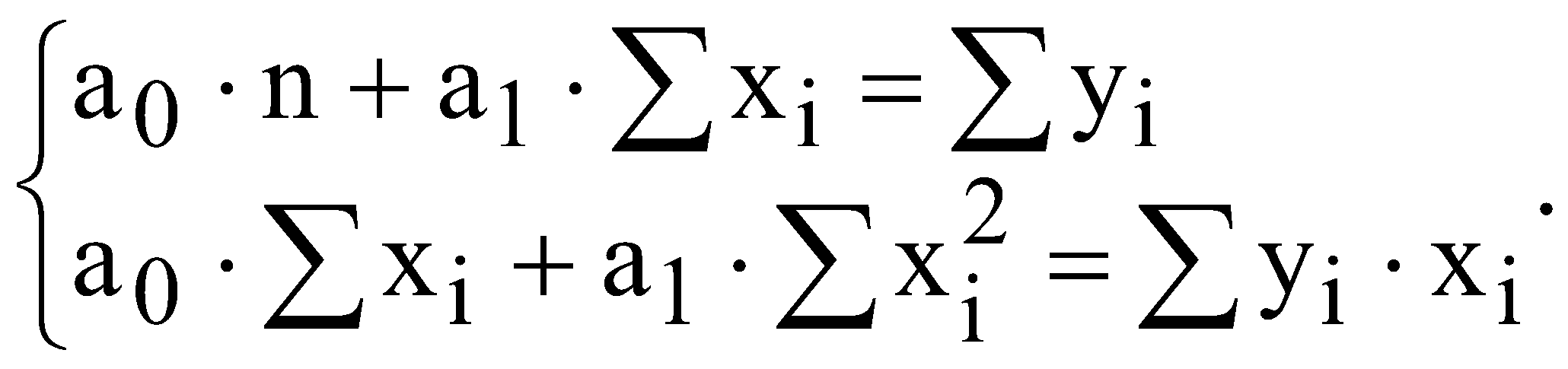 (5.7) (5.7)Критерій Фішера (F-критерій) визначається за формулою 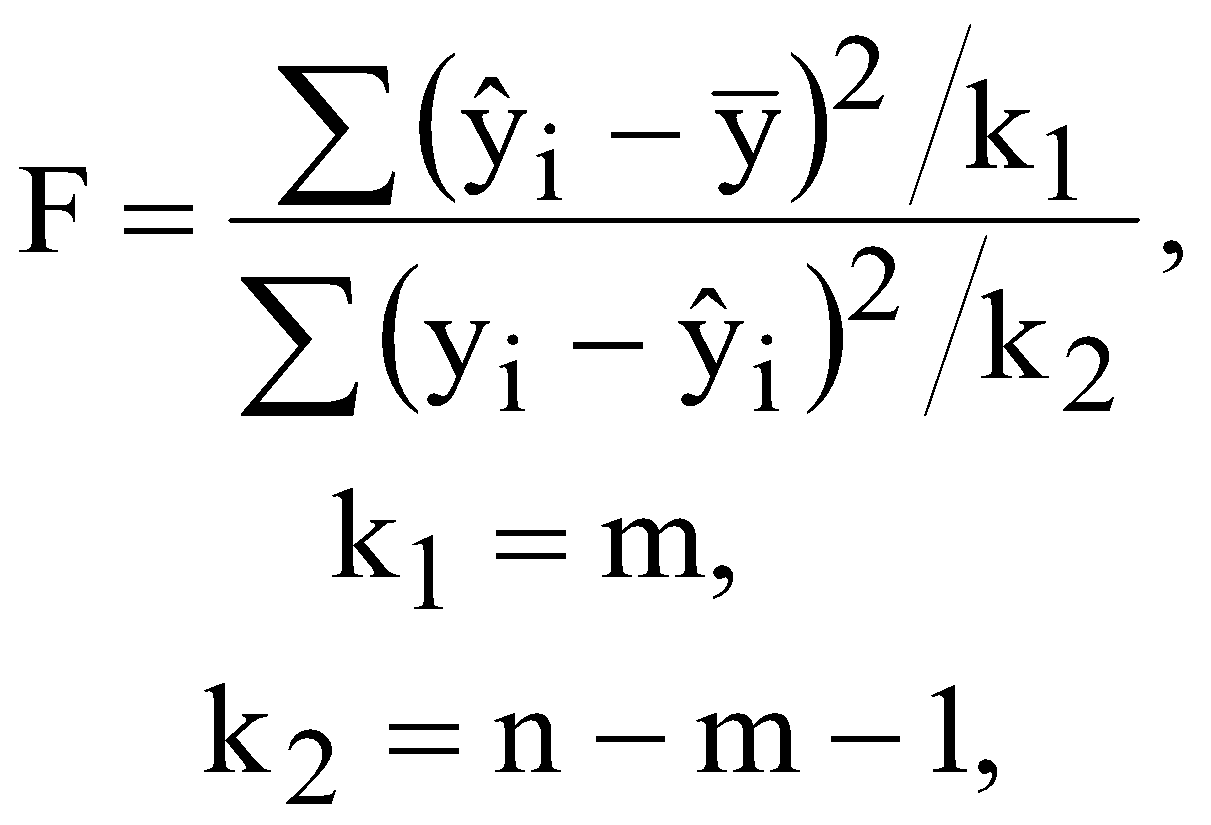 (5.8) (5.8)де m – кількість незалежних змінних; n - кількість спостережень. За статистичними таблицями F-розподілу з ступенями вільності k1 та k2 при заданому рівні ймовірності знаходимо значення В економетричних моделях особливе значення має автокореляція залишків (відхилень). Автокореляція відхилень – це кореляція відхилень від лінії регресії з відхиленнями від цієї лінії регресії, взятими з деяким запізненням, тобто це кореляція ряду Причини автокореляції залишків можуть бути різними, а саме недостатня статистична база для побудови економетричної моделі; ігнорування при побудові моделі істотного фактора; використання не відповідних форм залежності; статистичні дані зібрані з великими похибками. Для оцінки автокореляції залишків використовується критерій Дарбіна-Уотсона 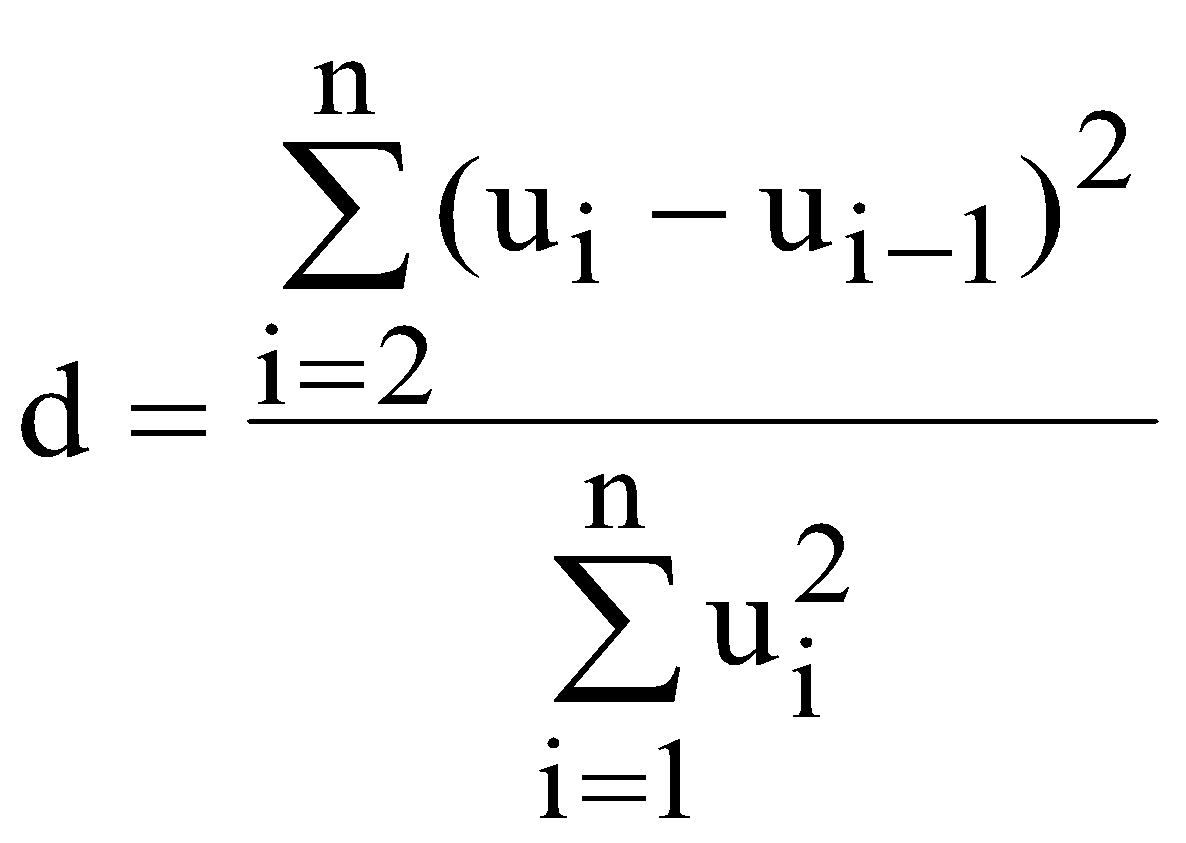 , , |
