Mt_ЕММ_lab_MK. Методичні вказівки до виконання лабораторних робіт для студентів першого (бакалаврського) рівня вищої освіти
 Скачать 3.77 Mb. Скачать 3.77 Mb.
|
|
ЛАБОРАТОРНА РОБОТА №10 ПОБУДОВА МОДЕЛІ ТРАНСПОРТНОЇ ЗАДАЧІ ТА ЇЇ АНАЛІЗ І. Загальні положення Існує доволі широке коло задач математичного програмування, в економіко-математичних моделях яких одна або кілька змінних мають набувати цілих значень. До таких задач можна віднести транспортну задачу. Класична транспортна задача – задача про найбільш економний план перевезення однорідного продукту чи взаємозамінних продуктів з пунктів виробництва в пункти споживання. Транспортна задача належить до типу розподільчих задач лінійного програмування. Економічний зміст таких задач може стосуватися різноманітних проблем, що переважно зовсім не пов’язано із перевезенням вантажів, як, наприклад, задачі оптимального розміщення виробництва, складів, оптимального призначення тощо. ІІ. Теоретичні відомості Класична транспортна задача лінійного програмування формулюється так: деякий однорідний продукт, що знаходиться у m постачальників Аі в обсягах 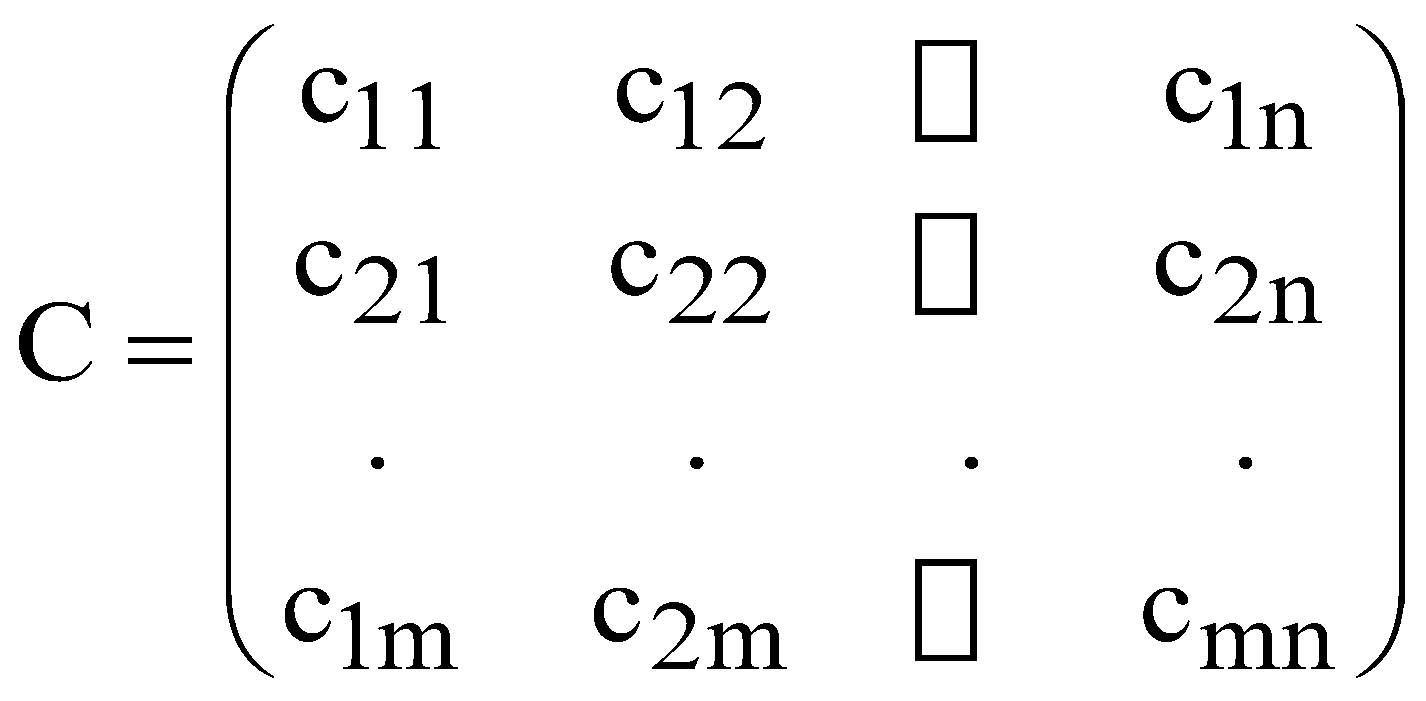 . .Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімальною. Вантаж, що перевозиться має бути однорідним, а одиниці виміру кількості продукції (вантажу) можуть бути різними (т, м3, шт., л тощо). Вартість перевезень виміряється в грошових одиницях, передбачається, що вартість перевезень продукції пропорційна його кількості. Постачальниками можуть бути підприємства, бази, склади, а споживачами – підприємства, магазини, будівельні об’єкти тощо. У такій постановці задачі ефективність плану перевезень визначається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень. Запишемо її математичну модель. Позначимо через Таблиця 10.1  Умова транспортної задачі Умова транспортної задачі
Мають виконуватися такі умови: сумарний обсяг продукції, що вивозиться з кожного і-го пункту, має дорівнювати запасу продукції в даному пункті 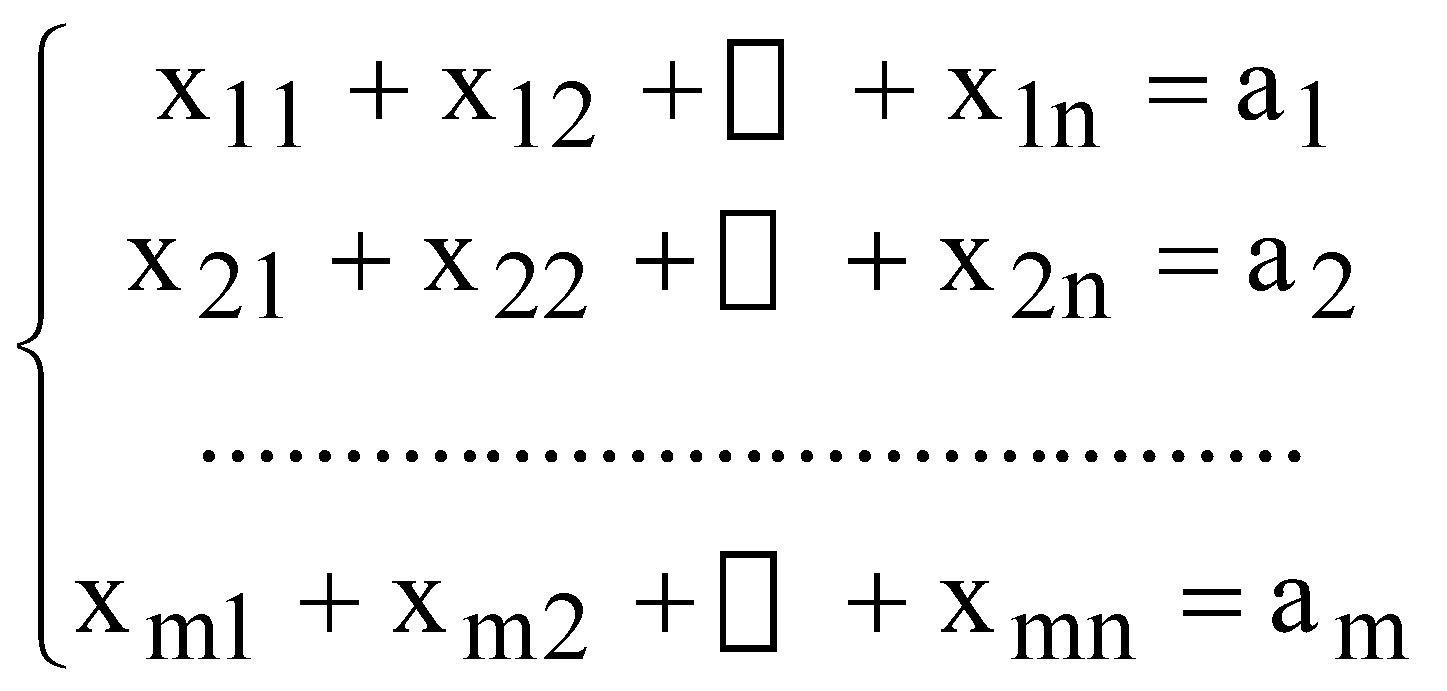 ; ;сумарний обсяг продукції, що ввезений кожному j-му споживачеві, має дорівнювати його потребам 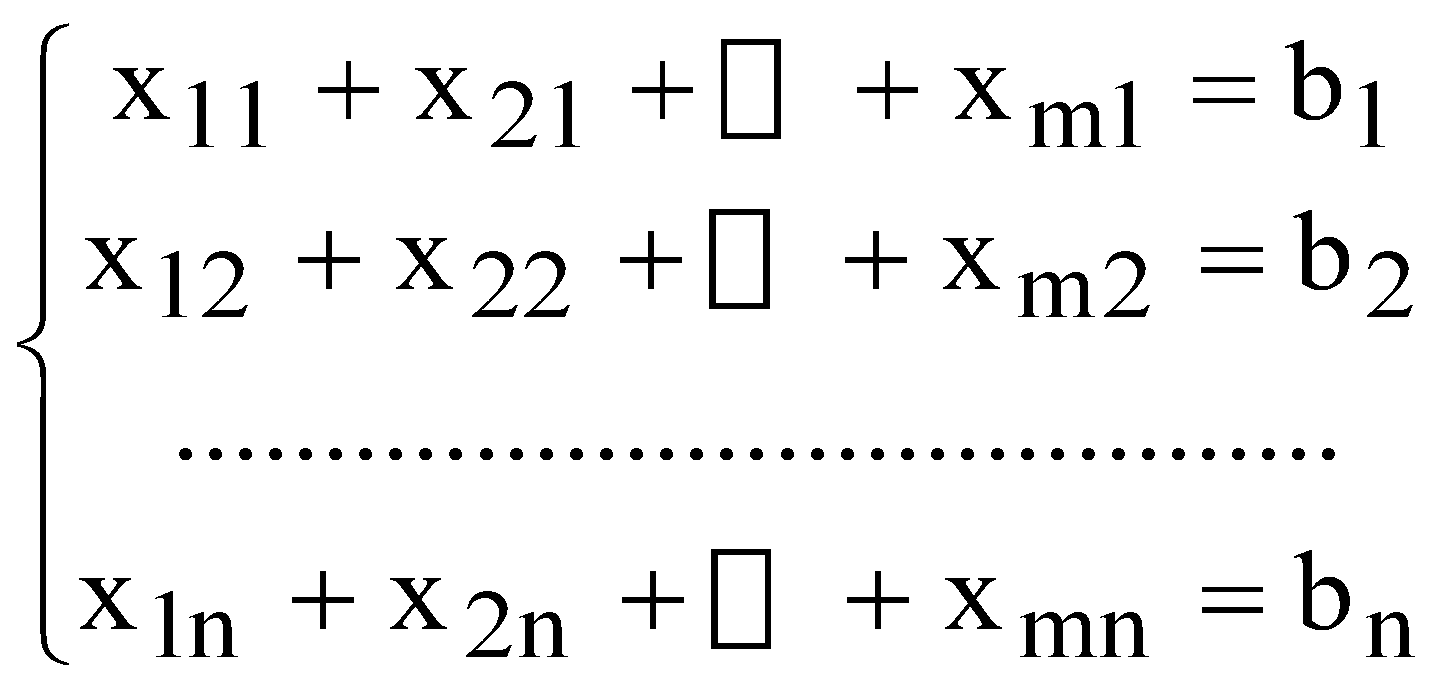 ; ;сумарна вартість всіх перевезень повинна бути мінімальною 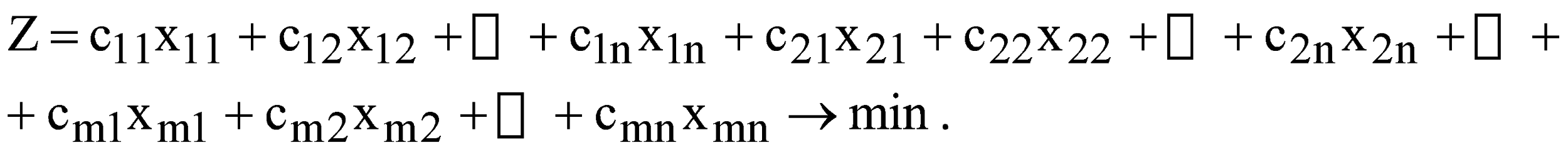 Очевидно, що У скороченій формі запису математична модель транспортної задачі за критерієм вартості перевезень має такий вигляд 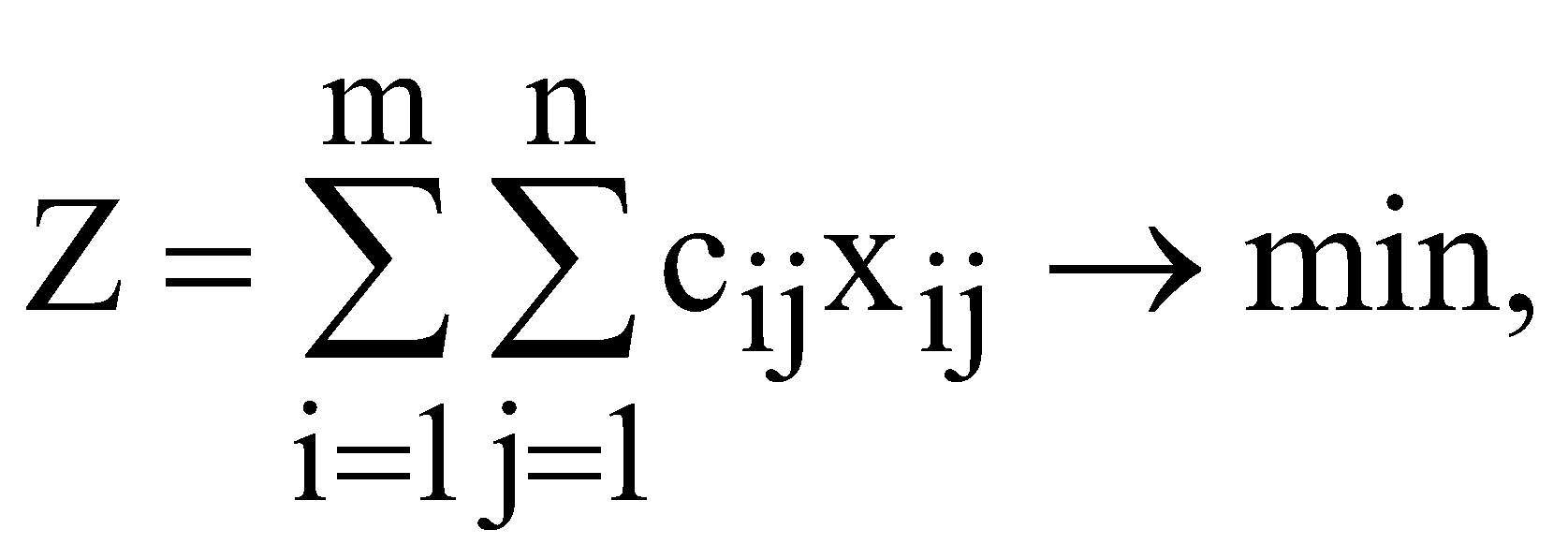 (10.1) (10.1)за обмежень: 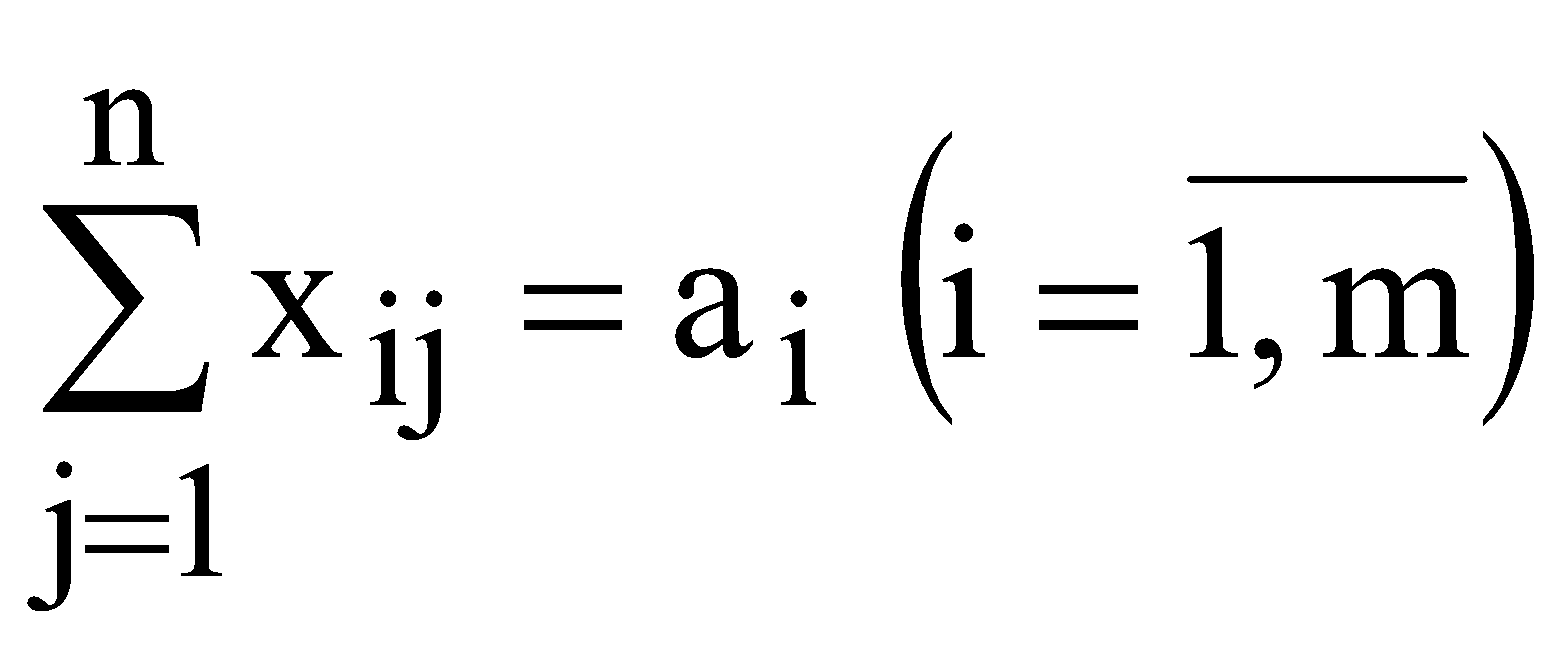 ; (10.2) ; (10.2)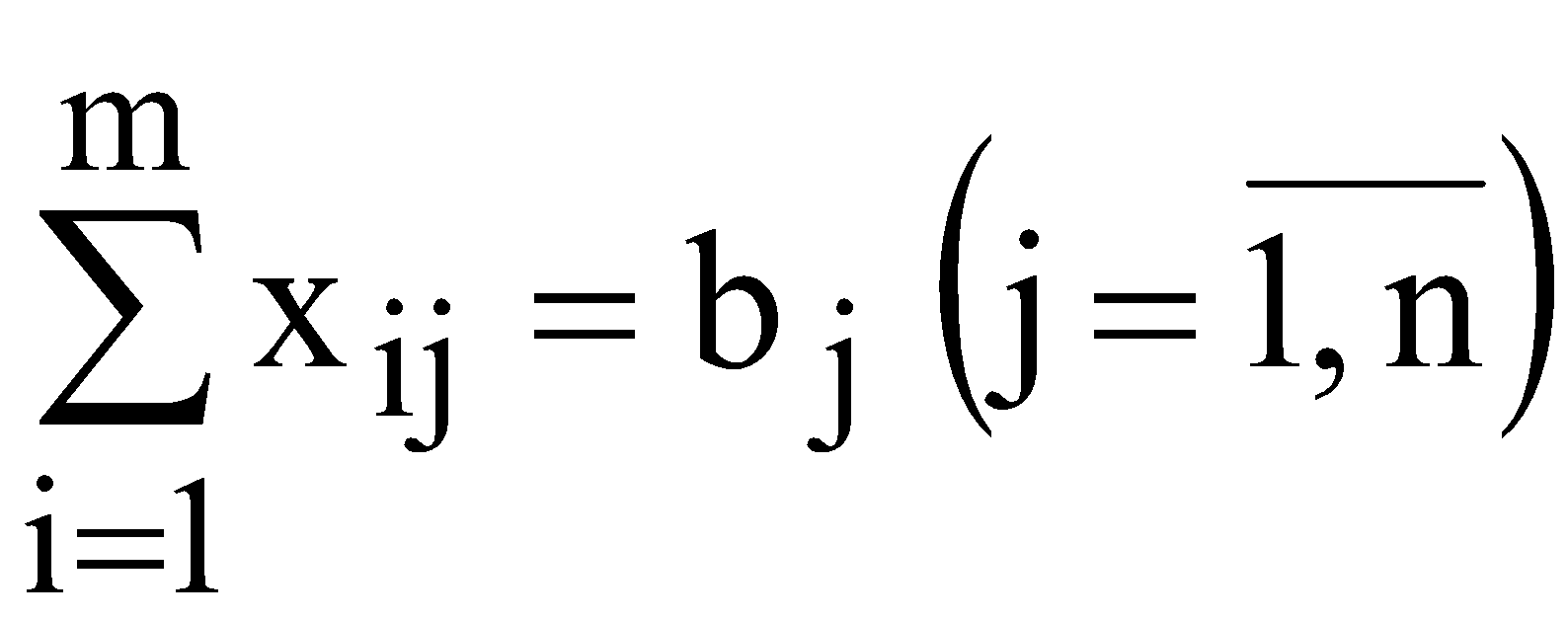 ; (10.3) ; (10.3)У розглянутій задачі має виконуватися умова: 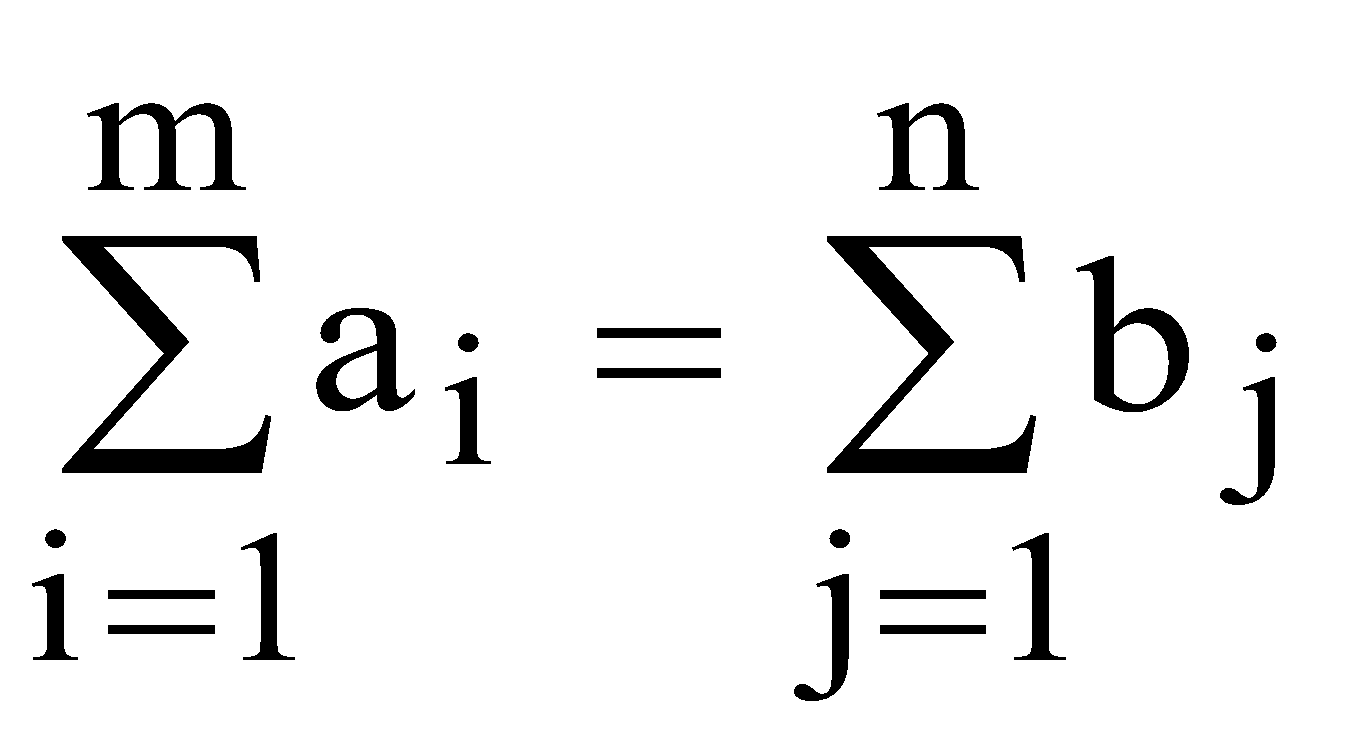 . (10.5) . (10.5)Транспортну задачу називають збалансованою, або закритою, якщо виконується умова (10.5). Якщо ж така умова не виконується, то транспортну задачу називають незбалансованою, або відкритою. На практиці при перевезенні продукції можлива одна з трьох ситуацій: 1) кількість одиниць вантажу в постачальників відповідає попиту з боку споживачів, що відображається в умові балансу як виконання рівності загальної суми запасу продукції загальній сумі потреб в ньому; 2) кількість вантажу в усіх постачальників більша за попит у цьому вантажу споживачів, тому частина вантажу в постачальників залишиться, а споживачі отримають увесь необхідний вантаж; 3) кількість вантажу в усіх постачальників менша від потреби в ньому всіх споживачів, тому кожен постачальник увесь свій вантаж вивезе, а частина споживачів отримує вантажу в меншій кількості, ніж необхідно. Найбільш простою і поширеною є збалансована (закрита) модель транспортної задачі. ІІІ. Завдання ПАТ "Срібні джерела" займається виробництвом та продажем мінеральної та солодкої води в Західному регіоні. Стандартні пляшки місткістю 1 л наповнюються напоями і далі надходять до пакувальної ділянки. Щодня з пакувальної ділянки відправляється 20 000 упакувань по 12 пляшок кожна. З пакувальної ділянки продукція направляється на склади підприємства, які розташовані у місці концентрації основних споживачів і є географічно віддаленими від місця розливу та пакування. ПАТ "Срібні джерела" володіє 2 складами, загальна потужність яких 60 000 упакувань в тиждень. Зі складу місцеві доставки до конкретних споживачів здійснюються самим підприємством власним парком невеликих фургонів, які можуть розвозити будь-які види продукції зі складу. Загальна потужність фургонів відповідає потужності складів і навіть її перевищує. Продукція ПАТ "Срібні джерела" доставляється споживачам через низку гуртівень та роздрібних магазинів. Кожен посередник може обслуговуватись із будь-якого складу. Дані про потреби посередників та тарифи перевезень подані в табл. 10.2. Таблиця 10.2 Дані про потреби посередників та тарифи перевезень
Необхідно визначити посередників, яких обслуговуватиме склад 1 та склад 2 відповідно, враховуючи, що потужність складу 1 складає 300000 пляшок/тиждень, а складу 2 - 420000 пляшок/тиждень, щоб досягнути мінімуму витрат на транспортування при повному задоволенні споживачів. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
